10.11: Self Inductance
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section we are dealing with the self inductance of a single coil rather than the mutual inductance between two coils. If the current through a single coil changes, the magnetic field inside that coil will change; consequently a back EMF will be induced in the coil that will oppose the change in the magnetic field and indeed will oppose the change of current.
Definition: coefficient of self inductance
The ratio of the back EMF to the rate of change of current is the coefficient of self inductance L. If the back EMF is 1 volt when the current changes at a rate of one amp per metre, the coefficient of self inductance is 1 henry.
Show that the coefficient of self inductance (usually called simply the "inductance") of a long solenoid of length l and having n turns per unit length is \mu n^2 Al, where I'm sure you know what all the symbols stand for. Put some numbers in for an imaginary solenoid of your own choosing, and calculate its inductance in henrys.
The circuit symbol for inductance is
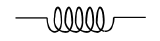 .
.
If a coil has an iron core, this may be indicated in the circuit by
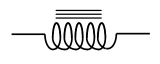 .
.
The symbol for a transformer is
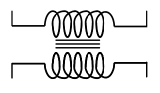 .
.
Finally, don't confuse self-inductance with self-indulgence.


