2.5: Heat Engines and the Second Law of Thermodynamics

$\newcommand\bes{\begin{equation}\begin{split}}$
$\newcommand\ltwid{\propto}$
$\newcommand\ees{\end{split}\end{equation}}$
$\newcommand\mib{\mathbf}$
$\newcommand\Sa{\textsf a}$
$\newcommand\Sb{\textsf b}$
$\newcommand\Sc{\textsf c}$
$\newcommand\Sd{\textsf d}$
$\newcommand\Se{\textsf e}$
$\newcommand\Sf{\textsf f}$
$\newcommand\Sg{\textsf g}$
$\newcommand\Sh{\textsf h}$
$\newcommand\Si{\textsf i}$
$\newcommand\Sj{\textsf j}$
$\newcommand\Sk{\textsf k}$
$\newcommand\Sl{\textsf l}$
$\newcommand\Sm{\textsf m}$
$\newcommand\Sn{\textsf n}$
$\newcommand\So{\textsf o}$
$\newcommand\Sp{\textsf p}$
$\newcommand\Sq{\textsf q}$
$\newcommand\Sr{\textsf r}$
$\newcommand\Ss{\textsf s}$
$\newcommand\St{\textsf t}$
$\newcommand\Su{\textsf u}$
$\newcommand\Sv{\textsf v}$
$\newcommand\Sw{\textsf w}$
$\newcommand\Sx{\textsf x}$
$\newcommand\Sy{\textsf y}$
$\newcommand\Sz{\textsf z}$
$\newcommand\SA{\textsf A}$
$\newcommand\SB{\textsf B}$
$\newcommand\SC{\textsf C}$
$\newcommand\SD{\textsf D}$
$\newcommand\SE{\textsf E}$
$\newcommand\SF{\textsf F}$
$\newcommand\SG{\textsf G}$
$\newcommand\SH{\textsf H}$
$\newcommand\SI{\textsf I}$
$\newcommand\SJ{\textsf J}$
$\newcommand\SK{\textsf K}$
$\newcommand\SL{\textsf L}$
$\newcommand\SM{\textsf M}$
$\newcommand\SN{\textsf N}$
$\newcommand\SO{\textsf O}$
$\newcommand\SP{\textsf P}$
$\newcommand\SQ{\textsf Q}$
$\newcommand\SR{\textsf R}$
$\newcommand\SS{\textsf S}$
$\newcommand\ST{\textsf T}$
$\newcommand\SU{\textsf U}$
$\newcommand\SV{\textsf V}$
$\newcommand\SW{\textsf W}$
$\newcommand\SX{\textsf X}$
$\newcommand\SY{\textsf Y}$
$\newcommand\SZ{\textsf Z}$
$\newcommand\Ha{\hat a}$
$\newcommand\Hb{\hat b}$
$\newcommand\Hc{\hat c}$
$\newcommand\Hd{\hat d}$
$\newcommand\He{\hat e}$
$\newcommand\Hf{\hat f}$
$\newcommand\Hg{\hat g}$
$\newcommand\Hh{\hat h}$
$\newcommand\Hi{\hat \imath}$
$\newcommand\Hj{\hat \jmath}$
$\newcommand\Hk{\hat k}$
$\newcommand\Hl{\hat l}$
$\newcommand\Hm{\hat m}$
$\newcommand\Hn{\hat n}$
$\newcommand\Ho{\hat o}$
$\newcommand\Hp{\hat p}$
$\newcommand\Hq{\hat q}$
$\newcommand\Hr{\hat r}$
$\newcommand\Hs{\hat s}$
$\newcommand\Ht{\hat t}$
$\newcommand\Hu{\hat u}$
$\newcommand\Hv{\hat v}$
$\newcommand\Hw{\hat w}$
$\newcommand\Hx{\hat x}$
$\newcommand\Hy{\hat y}$
$\newcommand\Hz{\hat z}$
$\newcommand\HA{\hat A}$
$\newcommand\HB{\hat B}$
$\newcommand\HC{\hat C}$
$\newcommand\HD{\hat D}$
$\newcommand\HE{\hat E}$
$\newcommand\HF{\hat F}$
$\newcommand\HG{\hat G}$
$\newcommand\HH{\hat H}$
$\newcommand\HI{\hat I}$
$\newcommand\HJ{\hat J}$
$\newcommand\HK{\hat K}$
$\newcommand\HL{\hat L}$
$\newcommand\HM{\hat M}$
$\newcommand\HN{\hat N}$
$\newcommand\HO{\hat O}$
$\newcommand\HP{\hat P}$
$\newcommand\HQ{\hat Q}$
$\newcommand\HR{\hat R}$
$\newcommand\HS{\hat S}$
$\newcommand\HT{\hat T}$
$\newcommand\HU{\hat U}$
$\newcommand\HV{\hat V}$
$\newcommand\HW{\hat W}$
$\newcommand\HX{\hat X}$
$\newcommand\HY{\hat Y}$
$\newcommand\HZ{\hat Z}$
$\newcommand\Halpha{\hat\alpha}$
$\newcommand\Hbeta{\hat\beta}$
$\newcommand\Hgamma{\hat\gamma}$
$\newcommand\Hdelta{\hat\delta}$
$\newcommand\Hepsilon{\hat\epsilon}$
$\newcommand\Hvarepsilon{\hat\varepsilon}$
$\newcommand\Hzeta{\hat\zeta}$
$\newcommand\Heta{\hat\eta}$
$\newcommand\Htheta{\hat\theta}$
$\newcommand\Hvartheta{\hat\vartheta}$
$\newcommand\Hiota{\hat\iota}$
$\newcommand\Hkappa{\hat\kappa}$
$\newcommand\Hlambda{\hat\lambda}$
$\newcommand\Hmu{\hat\mu}$
$\newcommand\Hnu{\hat\nu}$
$\newcommand\Hxi{\hat\xi}$
$\newcommand\Hom{\hat\omicron}$
$\newcommand\Hpi{\hat\pi}$
$\newcommand\Hvarpi{\hat\varpi}$
$\newcommand\Hrho{\hat\rho}$
$\newcommand\Hvarrho{\hat\varrho}$
$\newcommand\Hsigma{\hat\sigma}$
$\newcommand\Hvarsigma{\hat\varsigma}$
$\newcommand\Htau{\var\tau}$
$\newcommand\Hupsilon{\hat\upsilon}$
$\newcommand\Hphi{\hat\phi}$
$\newcommand\Hvarphi{\hat\varphi}$
$\newcommand\Hchi{\hat\chi}$
$\newcommand\Hxhi{\hat\xhi}$
$\newcommand\Hpsi{\hat\psi}$
$\newcommand\Homega{\hat\omega}$
$\newcommand\HGamma{\hat\Gamma}$
$\newcommand\HDelta{\hat\Delta}$
$\newcommand\HTheta{\hat\Theta}$
$\newcommand\HLambda{\hat\Lambda}$
$\newcommand\HXi{\hat\Xi}$
$\newcommand\HPi{\hat\Pi}$
$\newcommand\HSigma{\hat\Sigma}$
$\newcommand\HUps{\hat\Upsilon}$
$\newcommand\HPhi{\hat\Phi}$
$\newcommand\HPsi{\hat\Psi}$
$\newcommand\HOmega{\hat\Omega}$
$\newcommand\xhat{\hat\Bx}$
$\newcommand\yhat{\hat\By}$
$\newcommand\zhat{\hat\Bz}$
$\newcommand\ehat{\hat\Be}$
$\newcommand\khat{\hat\Bk}$
$\newcommand\nhat{\hat\Bn}$
$\newcommand\rhat{\hat\Br}$
$\newcommand\phihat{\hat\Bphi}$
$\newcommand\thetahat{\hat\Btheta}$
$\newcommand\MA{\mathbb A}$
$\newcommand\MB{\mathbb B}$
$\newcommand\MC{\mathbb C}$
$\newcommand\MD{\mathbb D}$
$\newcommand\ME{\mathbb E}$
$\newcommand\MF{\mathbb F}$
$\newcommand\MG{\mathbb G}$
$\newcommand\MH{\mathbb H}$
$\newcommand\MI{\mathbb I}$
$\newcommand\MJ{\mathbb J}$
$\newcommand\MK{\mathbb K}$
$\newcommand\ML{\mathbb L}$
$\newcommand\MM{\mathbb M}$
$\newcommand\MN{\mathbb N}$
$\newcommand\MO{\mathbb O}$
$\newcommand\MP{\mathbb P}$
$\newcommand\MQ{\mathbb Q}$
$\newcommand\MR{\mathbb R}$
$\newcommand\MS{\mathbb S}$
$\newcommand\MT{\mathbb T}$
$\newcommand\MU{\mathbb U}$
$\newcommand\MV{\mathbb V}$
$\newcommand\MW{\mathbb W}$
$\newcommand\MX{\mathbb X}$
$\newcommand\MY{\mathbb Y}$
$\newcommand\MZ{\mathbb Z}$
$\newcommand\CA{\mathcal A}$
$\newcommand\CB{\mathcal B}$
$\newcommand\CC{\mathcal C}$
$\newcommand\CD{\mathcal D}$
$\newcommand\CE{\mathcal E}$
$\newcommand\CF{\mathcal F}$
$\newcommand\CG{\mathcal G}$
$\newcommand\CH{\mathcal H}$
$\newcommand\CI{\mathcal I}$
$\newcommand\CJ{\mathcal J}$
$\newcommand\CK{\mathcal K}$
$\newcommand\CL{\mathcal L}$
$\newcommand\CM{\mathcal M}$
$\newcommand\CN{\mathcal N}$
$\newcommand\CO{\mathcal O}$
$\newcommand\CP{\mathcal P}$
$\newcommand\CQ{\mathcal Q}$
$\newcommand\CR{\mathcal R}$
$\newcommand\CS{\mathcal S}$
$\newcommand\CT{\mathcal T}$
$\newcommand\CU{\mathcal U}$
$\newcommand\CV{\mathcal V}$
$\newcommand\CW{\mathcal W}$
$\newcommand\CX{\mathcal X}$
$\newcommand\CY{\mathcal Y}$
$\newcommand\CZ{\mathcal Z}$
$\newcommand\Fa{\mathfrak a}$
$\newcommand\Fb{\mathfrak b}$
$\newcommand\Fc{\mathfrak c}$
$\newcommand\Fd{\mathfrak d}$
$\newcommand\Fe{\mathfrak e}$
$\newcommand\Ff{\mathfrak f}$
$\newcommand\Fg{\mathfrak g}$
$\newcommand\Fh{\mathfrak h}$
$\newcommand\Fi{\mathfrak i}$
$\newcommand\Fj{\mathfrak j}$
$\newcommand\Fk{\mathfrak k}$
$\newcommand\Fl{\mathfrak l}$
$\newcommand\Fm{\mathfrak m}$
$\newcommand\Fn{\mathfrak n}$
$\newcommand\Fo{\mathfrak o}$
$\newcommand\Fp{\mathfrak p}$
$\newcommand\Fq{\mathfrak q}$
$\newcommand\Fr{\mathfrak r}$
$\newcommand\Fs{\mathfrak s}$
$\newcommand\Ft{\mathfrak t}$
$\newcommand\Fu{\mathfrak u}$
$\newcommand\Fv{\mathfrak v}$
$\newcommand\Fw{\mathfrak w}$
$\newcommand\Fx{\mathfrak x}$
$\newcommand\Fy{\mathfrak y}$
$\newcommand\Fz{\mathfrak z}$
$\newcommand\FA{\mathfrak A}$
$\newcommand\FB{\mathfrak B}$
$\newcommand\FC{\mathfrak C}$
$\newcommand\FD{\mathfrak D}$
$\newcommand\FE{\mathfrak E}$
$\newcommand\FF{\mathfrak F}$
$\newcommand\FG{\mathfrak G}$
$\newcommand\FH{\mathfrak H}$
$\newcommand\FI{\mathfrak I}$
$\newcommand\FJ{\mathfrak J}$
$\newcommand\FK{\mathfrak K}$
$\newcommand\FL{\mathfrak L}$
$\newcommand\FM{\mathfrak M}$
$\newcommand\FN{\mathfrak N}$
$\newcommand\FO{\mathfrak O}$
$\newcommand\FP{\mathfrak P}$
$\newcommand\FQ{\mathfrak Q}$
$\newcommand\FR{\mathfrak R}$
$\newcommand\FS{\mathfrak S}$
$\newcommand\FT{\mathfrak T}$
$\newcommand\FU{\mathfrak U}$
$\newcommand\FV{\mathfrak V}$
$\newcommand\FW{\mathfrak W}$
$\newcommand\FX{\mathfrak X}$
$\newcommand\FY{\mathfrak Y}$
$\newcommand\FZ{\mathfrak Z}$
$\newcommand\Da{\dot a}$
$\newcommand\Db{\dot b}$
$\newcommand\Dc{\dot c}$
$\newcommand\Dd{\dot d}$
$\newcommand\De{\dot e}$
$\newcommand\Df{\dot f}$
$\newcommand\Dg{\dot g}$
$\newcommand\Dh{\dot h}$
$\newcommand\Di{\dot \imath}$
$\newcommand\Dj{\dot \jmath}$
$\newcommand\Dk{\dot k}$
$\newcommand\Dl{\dot l}$
$\newcommand\Dm{\dot m}$
$\newcommand\Dn{\dot n}$
$\newcommand\Do{\dot o}$
$\newcommand\Dp{\dot p}$
$\newcommand\Dq{\dot q}$
$\newcommand\Dr{\dot r}$
$\newcommand\Ds{\dot s}$
$\newcommand\Dt{\dot t}$
$\newcommand\Du{\dot u}$
$\newcommand\Dv{\dot v}$
$\newcommand\Dw{\dot w}$
$\newcommand\Dx{\dot x}$
$\newcommand\Dy{\dot y}$
$\newcommand\Dz{\dot z}$
$\newcommand\DA{\dot A}$
$\newcommand\DB{\dot B}$
$\newcommand\DC{\dot C}$
$\newcommand\DD{\dot D}$
$\newcommand\DE{\dot E}$
$\newcommand\DF{\dot F}$
$\newcommand\DG{\dot G}$
$\newcommand\DH{\dot H}$
$\newcommand\DI{\dot I}$
$\newcommand\DJ{\dot J}$
$\newcommand\DK{\dot K}$
$\newcommand\DL{\dot L}$
$\newcommand\DM{\dot M}$
$\newcommand\DN{\dot N}$
$\newcommand\DO{\dot O}$
$\newcommand\DP{\dot P}$
$\newcommand\DQ{\dot Q}$
$\newcommand\DR{\dot R}$
$\newcommand\DS{\dot S}$
$\newcommand\DT{\dot T}$
$\newcommand\DU{\dot U}$
$\newcommand\DV{\dot V}$
$\newcommand\DW{\dot W}$
$\newcommand\DX{\dot X}$
$\newcommand\DY{\dot Y}$
$\newcommand\DZ{\dot Z}$
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
$\newcommand\Dmu{\dot\mu}$
$\newcommand\Dnu{\dot\nu}$
$\newcommand\Dxi{\dot\xi}$
$\newcommand\Dom{\dot\omicron}$
$\newcommand\Dpi{\dot\pi}$
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
$\newcommand\Drho{\dot\rho}$
$\newcommand\Dvarrho{\dot\varrho}$
$\newcommand\Dsigma{\dot\sigma}$
$\newcommand\Dvarsigma{\dot\varsigma}$
$\newcommand\Dtau{\var\tau}$
$\newcommand\Dupsilon{\dot\upsilon}$
$\newcommand\Dphi{\dot\phi}$
$\newcommand\Dvarphi{\dot\varphi}$
$\newcommand\Dchi{\dot\chi}$
$\newcommand\Dpsi{\dot\psi}$
$\newcommand\Domega{\dot\omega}$
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
$\newcommand\DLambda{\dot\Lambda}$
$\newcommand\DXi{\dot\Xi}$
$\newcommand\DPi{\dot\Pi}$
$\newcommand\DSigma{\dot\Sigma}$
$\newcommand\DUps{\dot\Upsilon}$
$\newcommand\DPhi{\dot\Phi}$
$\newcommand\DPsi{\dot\Psi}$
$\newcommand\DOmega{\dot\Omega}$
$\newcommand\Va{\vec a}$
$\newcommand\Vb{\vec b}$
$\newcommand\Vc{\vec c}$
$\newcommand\Vd{\vec d}$
$\newcommand\Ve{\vec e}$
$\newcommand\Vf{\vec f}$
$\newcommand\Vg{\vec g}$
$\newcommand\Vh{\vec h}$
$\newcommand\Vi{\vec \imath}$
$\newcommand\Vj{\vec \jmath}$
$\newcommand\Vk{\vec k}$
$\newcommand\Vl{\vec l}$
$\newcommand\Vm{\vec m}$
$\newcommand\Vn{\vec n}$
$\newcommand\Vo{\vec o}$
$\newcommand\Vp{\vec p}$
$\newcommand\Vq{\vec q}$
$\newcommand\Vr{\vec r}$
$\newcommand\Vs{\vec s}$
$\newcommand\Vt{\vec t}$
$\newcommand\Vu{\vec u}$
$\newcommand\Vv{\vec v}$
$\newcommand\Vw{\vec w}$
$\newcommand\Vx{\vec x}$
$\newcommand\Vy{\vec y}$
$\newcommand\Vz{\vec z}$
$\newcommand\VA{\vec A}$
$\newcommand\VB{\vec B}$
$\newcommand\VC{\vec C}$
$\newcommand\VD{\vec D}$
$\newcommand\VE{\vec E}$
$\newcommand\VF{\vec F}$
$\newcommand\VG{\vec G}$
$\newcommand\VH{\vec H}$
$\newcommand\VI{\vec I}$
$\newcommand\VJ{\vec J}$
$\newcommand\VK{\vec K}$
$\newcommand\VL{\vec L}$
$\newcommand\VM{\vec M}$
$\newcommand\VN{\vec N}$
$\newcommand\VO{\vec O}$
$\newcommand\VP{\vec P}$
$\newcommand\VQ{\vec Q}$
$\newcommand\VR{\vec R}$
$\newcommand\VS{\vec S}$
$\newcommand\VT{\vec T}$
$\newcommand\VU{\vec U}$
$\newcommand\VV{\vec V}$
$\newcommand\VW{\vec W}$
$\newcommand\VX{\vec X}$
$\newcommand\VY{\vec Y}$
$\newcommand\VZ{\vec Z}$
$\newcommand\Valpha{\vec\alpha}$
$\newcommand\Vbeta{\vec\beta}$
$\newcommand\Vgamma{\vec\gamma}$
$\newcommand\Vdelta{\vec\delta}$
$\newcommand\Vepsilon{\vec\epsilon}$
$\newcommand\Vvarepsilon{\vec\varepsilon}$
$\newcommand\Vzeta{\vec\zeta}$
$\newcommand\Veta{\vec\eta}$
$\newcommand\Vtheta{\vec\theta}$
$\newcommand\Vvartheta{\vec\vartheta}$
$\newcommand\Viota{\vec\iota}$
$\newcommand\Vkappa{\vec\kappa}$
$\newcommand\Vlambda{\vec\lambda}$
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
$\newcommand\VTheta{\vec\Theta}$
$\newcommand\VLambda{\vec\Lambda}$
$\newcommand\VXi{\vec\Xi}$
$\newcommand\VPi{\vec\Pi}$
$\newcommand\VSigma{\vec\Sigma}$
$\newcommand\VUps{\vec\Upsilon}$
$\newcommand\VPhi{\vec\Phi}$
$\newcommand\VPsi{\vec\Psi}$
$\newcommand\VOmega{\vec\Omega}$
$\newcommand\BA{\mib A}$
$\newcommand\BB{\mib B}$
$\newcommand\BC{\mib C}$
$\newcommand\BD{\mib D}$
$\newcommand\BE{\mib E}$
$\newcommand\BF{\mib F}$
$\newcommand\BG{\mib G}$
$\newcommand\BH{\mib H}$
$\newcommand\BI{\mib I}}$
$\newcommand\BJ{\mib J}$
$\newcommand\BK{\mib K}$
$\newcommand\BL{\mib L}$
$\newcommand\BM{\mib M}$
$\newcommand\BN{\mib N}$
$\newcommand\BO{\mib O}$
$\newcommand\BP{\mib P}$
$\newcommand\BQ{\mib Q}$
$\newcommand\BR{\mib R}$
$\newcommand\BS{\mib S}$
$\newcommand\BT{\mib T}$
$\newcommand\BU{\mib U}$
$\newcommand\BV{\mib V}$
$\newcommand\BW{\mib W}$
$\newcommand\BX{\mib X}$
$\newcommand\BY{\mib Y}$
$\newcommand\BZ{\mib Z}$
$\newcommand\Ba{\mib a}$
$\newcommand\Bb{\mib b}$
$\newcommand\Bc{\mib c}$
$\newcommand\Bd{\mib d}$
$\newcommand\Be{\mib e}$
$\newcommand\Bf{\mib f}$
$\newcommand\Bg{\mib g}$
$\newcommand\Bh{\mib h}$
$\newcommand\Bi{\mib i}$
$\newcommand\Bj{\mib j}$
$\newcommand\Bk{\mib k}$
$\newcommand\Bl{\mib l}$
$\newcommand\Bm{\mib m}$
$\newcommand\Bn{\mib n}$
$\newcommand\Bo{\mib o}$
$\newcommand\Bp{\mib p}$
$\newcommand\Bq{\mib q}$
$\newcommand\Br{\mib r}$
$\newcommand\Bs{\mib s}$
$\newcommand\Bt{\mib t}$
$\newcommand\Bu{\mib u}$
$\newcommand\Bv{\mib v}$
$\newcommand\Bw{\mib w}$
$\newcommand\Bx{\mib x}$
$\newcommand\By{\mib y}$
$\newcommand\Bz{\mib z}$\)
$\newcommand\vrh{\varrho}$
$\newcommand\vsig{\varsigma}$
$\newcommand\ups{\upsilon}$
$\newcommand\eps{\epsilon}$
$\newcommand\ve{\varepsilon}$
$\newcommand\vth{\vartheta}$
$\newcommand\vphi{\varphi}$
$\newcommand\xhi{\chi}$
$\newcommand\Ups{\Upsilon}$
$\newcommand\Balpha{\mib\alpha}$
$\newcommand\Bbeta{\mib\beta}$
$\newcommand\Bgamma{\mib\gamma}$
$\newcommand\Bdelta{\mib\delta}$
$\newcommand\Beps{\mib\epsilon}$
$\newcommand\Bve{\mib\varepsilon}$
$\newcommand\Bzeta{\mib\zeta}$
$\newcommand\Beta{\mib\eta}$
$\newcommand\Btheta{\mib\theta}$
$\newcommand\Bvth{\mib\vartheta}$
$\newcommand\Biota{\mib\iota}$
$\newcommand\Bkappa{\mib\kappa}$
$\newcommand\Blambda{\mib\lambda}$
$\newcommand\Bmu{\mib\mu}$
$\newcommand\Bnu{\mib\nu}$
$\newcommand\Bxi{\mib\xi}$
$\newcommand\Bom{\mib\omicron}$
$\newcommand\Bpi{\mib\pi}$
$\newcommand\Bvarpi{\mib\varpi}$
$\newcommand\Brho{\mib\rho}$
$\newcommand\Bvrh{\mib\varrho}$
$\newcommand\Bsigma{\mib\sigma}$
$\newcommand\Bvsig{\mib\varsigma}$
$\newcommand\Btau{\mib\tau}$
$\newcommand\Bups{\mib\upsilon}$
$\newcommand\Bphi{\mib\phi}$
$\newcommand\Bvphi{\mib\vphi}$
$\newcommand\Bchi{\mib\chi}$
$\newcommand\Bpsi{\mib\psi}$
$\newcommand\Bomega{\mib\omega}$
$\newcommand\BGamma{\mib\Gamma}$
$\newcommand\BDelta{\mib\Delta}$
$\newcommand\BTheta{\mib\Theta}$
$\newcommand\BLambda{\mib\Lambda}$
$\newcommand\BXi{\mib\Xi}$
$\newcommand\BPi{\mib\Pi}$
$\newcommand\BSigma{\mib\Sigma}$
$\newcommand\BUps{\mib\Upsilon}$
$\newcommand\BPhi{\mib\Phi}$
$\newcommand\BPsi{\mib\Psi}$
$\newcommand\BOmega{\mib\Omega}$
$\newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}$
$\newcommand\RGamma{ \Gamma}$
$\newcommand\RDelta{ \Delta}$
$\newcommand\RTheta{ \Theta}$
$\newcommand\RLambda{ \Lambda}$
$\newcommand\RXi{ \Xi}$
$\newcommand\RPi{ \Pi}$
$\newcommand\RSigma{ \Sigma}$
$\newcommand\RUps{ \Upsilon}$
$\newcommand\RPhi{ \Phi}$
$\newcommand\RPsi{ \Psi}$
$\newcommand\ROmega{ \Omega}$
$\newcommand\RA{ A}$
$\newcommand\RB{ B}$
$\newcommand\RC{ C}$
$\newcommand\RD{ D}$
$\newcommand\RE{ E}$
$\newcommand\RF{ F}$
$\newcommand\RG{ G}$
$\newcommand\RH{ H}$
$\newcommand\RI{ I}$
$\newcommand\RJ{ J}$
$\newcommand\RK{ K}$
$\newcommand\RL{ L}$
$\newcommand { M}$
$\newcommand\RN{ N}$
$\newcommand\RO{ O}$
$\newcommand\RP{ P}$
$\newcommand\RQ{ Q}$
$\newcommand\RR{ R}$
$\newcommand\RS{ S}$
$\newcommand\RT{ T}$
$\newcommand\RU{ U}$
$\newcommand\RV{ V}$
$\newcommand\RW{ W}$
$\newcommand\RX{ X}$
$\newcommand\RY{ Y}$
$\newcommand\RZ{ Z}$
$\newcommand\Ra{ a}$
$\newcommand\Rb{ b}$
$\newcommand\Rc{ c}$
$\newcommand\Rd{ d}$
$\newcommand\Re{ e}$
$\newcommand\Rf{ f}$
$\newcommand\Rg{ g}$
$\newcommand\Rh{ h}$
$\newcommand\Ri{ i}$
$\newcommand\Rj{ j}$
$\newcommand\Rk{ k}$
$\newcommand\Rl{ l}$
$\newcommand { m}$
$\newcommand\Rn{ n}$
$\newcommand\Ro{ o}$
$\newcommand\Rp{ p}$
$\newcommand\Rq{ q}$
$\newcommand\Rr{ r}$
$\newcommand\Rs{ s}$
$\newcommand\Rt{ t}$
$\newcommand\Ru{ u}$
$\newcommand\Rv{ v}$
$\newcommand\Rw{ w}$
$\newcommand\Rx{ x}$
$\newcommand\Ry{ y}$
$\newcommand\Rz{ z}$
$\newcommand\BBA{\boldsymbol\RA}$
$\newcommand\BBB{\boldsymbol\RB}$
$\newcommand\BBC{\boldsymbol\RC}$
$\newcommand\BBD{\boldsymbol\RD}$
$\newcommand\BBE{\boldsymbol\RE}$
$\newcommand\BBF{\boldsymbol\RF}$
$\newcommand\BBG{\boldsymbol\RG}$
$\newcommand\BBH{\boldsymbol\RH}$
$\newcommand\BBI{\boldsymbol\RI}$
$\newcommand\BBJ{\boldsymbol\RJ}$
$\newcommand\BBK{\boldsymbol\RK}$
$\newcommand\BBL{\boldsymbol\RL}$
$\newcommand\BBM{\boldsymbol }$
$\newcommand\BBN{\boldsymbol\RN}$
$\newcommand\BBO{\boldsymbol\RO}$
$\newcommand\BBP{\boldsymbol\RP}$
$\newcommand\BBQ{\boldsymbol\RQ}$
$\newcommand\BBR{\boldsymbol\RR}$
$\newcommand\BBS{\boldsymbol\RS}$
$\newcommand\BBT{\boldsymbol\RT}$
$\newcommand\BBU{\boldsymbol\RU}$
$\newcommand\BBV{\boldsymbol\RV}$
$\newcommand\BBW{\boldsymbol\RW}$
$\newcommand\BBX{\boldsymbol\RX}$
$\newcommand\BBY{\boldsymbol\RY}$
$\newcommand\BBZ{\boldsymbol\RZ}$
$\newcommand\BBa{\boldsymbol\Ra}$
$\newcommand\BBb{\boldsymbol\Rb}$
$\newcommand\BBc{\boldsymbol\Rc}$
$\newcommand\BBd{\boldsymbol\Rd}$
$\newcommand\BBe{\boldsymbol\Re}$
$\newcommand\BBf{\boldsymbol\Rf}$
$\newcommand\BBg{\boldsymbol\Rg}$
$\newcommand\BBh{\boldsymbol\Rh}\}$
$\newcommand\BBi{\boldsymbol\Ri}$
$\newcommand\BBj{\boldsymbol\Rj}$
$\newcommand\BBk{\boldsymbol\Rk}$
$\newcommand\BBl{boldsymbol\Rl}$
$\newcommand\BBm{\boldsymbol }$
$\newcommand\BBn{\boldsymbol\Rn}$
$\newcommand\BBo{\boldsymbol\Ro}$
$\newcommand\BBp{\boldsymbol\Rp}$
$\newcommand\BBq{\boldsymbol\Rq}$
$\newcommand\BBr{\boldsymbol\Rr}$
$\newcommand\BBs{\boldsymbol\Rs}$
$\newcommand\BBt{\boldsymbol\Rt}$
$\newcommand\BBu{\boldsymbol\Ru}$
$\newcommand\BBv{\boldsymbol\Rv}$
$\newcommand\BBw{\boldsymbol\Rw}$
$\newcommand\BBx{\boldsymbol\Rx}$
$\newcommand\BBy{\boldsymbol\Ry}$
$\newcommand\BBz{\boldsymbol\Rz}$
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
$\newcommand\bnabla{\boldsymbol{\nabla}}$
$\newcommand\Bell{\boldsymbol\ell}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\newcommand\ns{^\vphantom{*}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}$
$\newcommand\izpi{\int\limits_{0}^{\infty}\!\!}$
$\newcommand\etc{\it etc.\/}$
$\newcommand\etal{\it et al.\/}$
$\newcommand\opcit{\it op. cit.\/}$
$\newcommand\ie{\it i.e.\/}$
$\newcommand\Ie{\it I.e.\/}$
$\newcommand\viz{\it viz.\/}$
$\newcommand\eg{\it e.g.\/}$
$\newcommand\Eg{\it E.g.\/}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\def\sss#1{\scriptscriptstyle #1}$
$\def\ss#1{\scriptstyle #1}$
$\def\ssr#1{\scriptstyle #1}$
$\def\ssf#1{\scriptstyle #1}$
$\newcommand\NA{N_{\ssr{\!A}}}$
$\newcommand\lala{\langle\!\langle}$
$\newcommand\rara{\rangle\!\rangle}$
$\newcommand\blan{\big\langle}$
$\newcommand\bran{\big\rangle}$
$\newcommand\Blan{\Big\langle}$
$\newcommand\Bran{\Big\rangle}$
$\newcommand\intl{\int\limits}$
$\newcommand\half{\frac{1}{2}}$
$\newcommand\third{\frac{1}{3}}$
$\newcommand\fourth{\frac{1}{4}}$
$\newcommand\eighth{\frac{1}{8}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\undertext#1{$\underline{\hbox{#1}}$}$
$\newcommand\Tra{\mathop{\textsf{Tr}}\,}$
$\newcommand\det{\mathop{\textsf{det}}\,}$
$\def\tket#1{|  #1 \rangle}$
$\def\tbra#1{\langle #1|}$
$\def\tbraket#1#2{\langle #1  |   #2 \rangle}$
$\def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}$
$\def\sket#1{|  \, #1 \,  \rangle}$
$\def\sbra#1{\langle \,  #1 \, |}$
$\def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}$
$\def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}$
$\def\ket#1{\big| \, #1\, \big\rangle}$
$\def\bra#1{\big\langle \, #1 \, \big|}$
$\def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}$
$\def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}$
$\newcommand\pz{\partial}$
$\newcommand\pzb{\bar{\partial}}$
$\newcommand\svph{\vphantom{\int}}$
$\newcommand\vph{\vphantom{\sum_i}}$
$\newcommand\bvph{\vphantom{\sum_N^N}}$
$\newcommand\nd{^{\vphantom{\dagger}}}$
$\newcommand\ns{^{\vphantom{*}}}$
$\newcommand\yd{^\dagger}$
$\newcommand\zb{\bar z}$
$\newcommand\zdot{\dot z}$
$\newcommand\zbdot{\dot{\bar z}}$
$\newcommand\kB{k_{\sss{B}}}$
$\newcommand\kT{k_{\sss{B}}T}$
$\newcommand\gtau{g_\tau}$
$\newcommand\Htil{\tilde H}$
$\newcommand\pairo{(\phi\nd_0,J\nd_0)}$
$\newcommand\pairm{(\phi\nd_0,J)}$
$\newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}$
$\newcommand\pairmb{(\Bphi\nd_0,\BJ)}$
$\newcommand\pair{(\phi,J)}$
$\newcommand\Hz{H\nd_0}$
$\newcommand\Ho{H\nd_1}$
$\newcommand\Htz{\Htil\nd_0}$
$\newcommand\Hto{\Htil\nd_1}$
$\newcommand\oc{\omega_\Rc}$

$\newcommand \gtwid{\approx}$

$\newcommand\index{\textsf{ind}}$
$\newcommand\csch{\,{ csch\,}}$
$\newcommand\ctnh{\,{ ctnh\,}}$
$\newcommand\ctn{\,{ ctn\,}}$
$\newcommand\sgn{\,{ sgn\,}}$
$\def\tmapright#1{\xrightarrow \limits^{#1}}$
$\def\bmapright#1{\xrightarrow\limits_{#1}}$
$\newcommand\hfb{\hfill\break}$
$\newcommand\Rep{\textsf{Re}\,}$
$\newcommand\Imp{\textsf{Im}\,}$
$\newcommand\ncdot{\!\cdot\!}$
$\def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }$
$\def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }$
$\newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}$

$\def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}$
$\def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}$
$\def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}$
$\def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}$
$\newcommand\subA{\ns_\ssr{A}}$
$\newcommand\subB{\ns_\ssr{B}}$
$\newcommand\subC{\ns_\ssr{C}}$
$\newcommand\subD{\ns_\ssr{D}}$
$\newcommand\subAB{\ns_\ssr{AB}}$
$\newcommand\subBC{\ns_\ssr{BC}}$
$\newcommand\subCD{\ns_\ssr{CD}}$
$\newcommand\subDA{\ns_\ssr{DA}}$
$\def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }$
$\def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}$
$\newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}$
$\newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}$
$\newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}$
$\newcommand\cds{\,\bullet\,}$
$\newcommand\ccs{\,\circ\,}$
$\newcommand\nsub{_{\vphantom{\dagger}}}$
$\newcommand\rhohat{\hat\rho}$
$\newcommand\vrhhat{\hat\vrh}$
$\newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}$
$\newcommand\brangle{\big\rangle}$
$\newcommand\blangle{\big\langle}$
$\newcommand\vet{\tilde\ve}$
$\newcommand\zbar{\bar z}$
$\newcommand\ftil{\tilde f}$
$\newcommand\XBE{\RXi\ns_\ssr{BE}}$
$\newcommand\XFD{\RXi\ns_\ssr{FD}}$
$\newcommand\OBE{\Omega\ns_\ssr{BE}}$
$\newcommand\OFD{\Omega\ns_\ssr{FD}}$
$\newcommand\veF{\ve\ns_\RF}$
$\newcommand\kF{k\ns_\RF}$
$\newcommand\kFu{k\ns_{\RF\uar}}$
$\newcommand\SZ{\textsf Z}}$ \( \newcommand\kFd{k\ns_{\RF\dar}\)
$\newcommand\muB{\mu\ns_\ssr{B}}$
$\newcommand\mutB{\tilde\mu}\ns_\ssr{B}$
$\newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}$
$\newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}$
$\newcommand\xhiOZ{\xhi^\ssr{OZ}}$
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
$\newcommand\jhz{\HJ(0)}$
$\newcommand\nda{\nd_\alpha}$
$\newcommand\ndap{\nd_{\alpha'}}$
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
$\newcommand\msa{m\ns_\ssr{A}}$
$\newcommand\msb{m\ns_\ssr{B}}$
$\newcommand\mss{m\ns_\Rs}$
$\newcommand\HBx{\hat\Bx}$
$\newcommand\HBy{\hat\By}$
$\newcommand\HBz{\hat\Bz}$
$\newcommand\thm{\theta\ns_m}$
$\newcommand\thp{\theta\ns_\phi}$
$\newcommand\mtil{\widetilde m}$
$\newcommand\phitil{\widetilde\phi}$
$\newcommand\delf{\delta\! f}$
$\newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}$
$\newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}$
$\newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}$
$\newcommand\vbar{\bar v}$
$\newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}$
$\newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}$
$\newcommand\gla{g\nd_{\RLambda\nd}}$
$\newcommand\TA{T\ns_\ssr{A}}$
$\newcommand\TB{T\ns_\ssr{B}}$
$\newcommand\ncdot{\!\cdot\!}$
$\newcommand\NS{N\ns_{\textsf S}}$

There’s no free lunch so quit asking

A heat engine is a device which takes a thermodynamic system through a repeated cycle which can be represented as a succession of equilibrium states: $\RA\to\RB\to\RC\cdots\to\RA$. The net result of such a cyclic process is to convert heat into mechanical work, or vice versa.

Figure [perfect]: A perfect engine would extract heat $Q$ from a thermal reservoir at some temperature $T$ and convert it into useful mechanical work $W$. This process is alas impossible, according to the Second Law of thermodynamics. The inverse process, where work $\CW$ is converted into heat $\CQ$, is always possible.

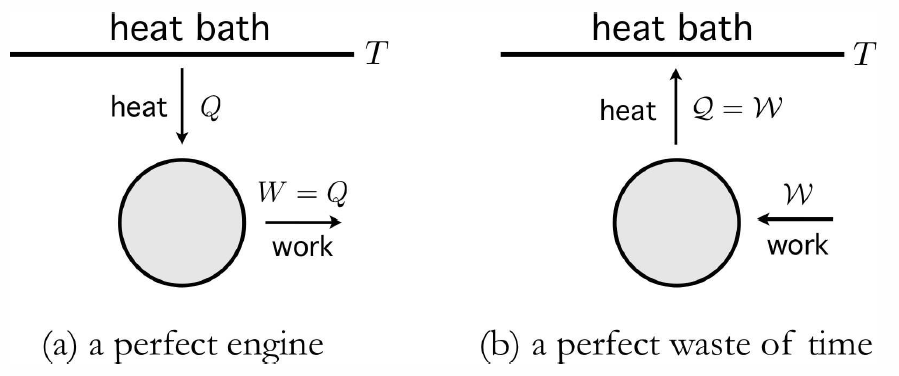
For a system in equilibrium at temperature $T$, there is a thermodynamically large amount of internal energy stored in the random internal motion of its constituent particles. Later, when we study statistical mechanics, we will see how each ‘quadratic’ degree of freedom in the Hamiltonian contributes $\half\kT$ to the total internal energy. An immense body in equilibrium at temperature $T$ has an enormous heat capacity $C$, hence extracting a finite quantity of heat $Q$ from it results in a temperature change $\RDelta T=-Q/C$ which is utterly negligible. Such a body is called a heat bath, or thermal reservoir. A perfect engine would, in each cycle, extract an amount of heat $Q$ from the bath and convert it into work. Since $\RDelta E=0$ for a cyclic process, the First Law then gives $W=Q$. This situation is depicted schematically in Fig. [perfect]. One could imagine running this process virtually indefinitely, slowly sucking energy out of an immense heat bath, converting the random thermal motion of its constituent molecules into useful mechanical work. Sadly, this is not possible:

A transformation whose only final result is to extract heat froma source at fixed temperature and transform that heat into work is impossible.

This is known as the Postulate of Lord Kelvin. It is equivalent to the postulate of Clausius,

A transformation whose only result is to transfer heat from a body at a given temperature to a body at higher temperature is impossible.

These postulates which have been repeatedly validated by empirical observations, constitute the Second Law of Thermodynamics.

Engines and refrigerators

While it is not possible to convert heat into work with 100% efficiency, it is possible to transfer heat from one thermal reservoir to another one, at lower temperature, and to convert some of that heat into work. This is what an engine does. The energy accounting for one cycle of the engine is depicted in the left hand panel of Fig. [engref]. An amount of heat $Q\ns_2>0$ is extracted- from the reservoir at temperature $T\ns_2$. Since the reservoir is assumed to be enormous, its temperature change $\RDelta T\ns_2=-Q\ns_2/C\ns_2$ is negligible, and its temperature remains constant – this is what it means for an object to be a reservoir. A lesser amount of heat, $\CQ\ns_1$, with $0 < \CQ\ns_1 < Q\ns_2$, is deposited in a second reservoir at a lower temperature $T\ns_1$. Its temperature change $\RDelta T\ns_1=+\CQ\ns_1/C\ns_1$ is also negligible. The difference $W=Q\ns_2-\CQ\ns_1$ is extracted as useful work. We define the efficiency, $\eta$, of the engine as the ratio of the work done to the heat extracted from the upper reservoir, per cycle:

$$\eta={W\over Q\ns_2}=1-{\CQ\ns_1\over Q\ns_2}\ .$$ This is a natural definition of efficiency, since it will cost us fuel to maintain the temperature of the upper reservoir over many cycles of the engine. Thus, the efficiency is proportional to the ratio of the work done to the cost of the fuel.

A refrigerator works according to the same principles, but the process runs in reverse. An amount of heat $Q_1$ is extracted from the lower reservoir – the inside of our refrigerator – and is pumped into the upper reservoir. As Clausius’ form of the Second Law asserts, it is impossible for this to be the only result of our cycle. Some amount of work $\CW$ must be performed on the refrigerator in order for it to extract the heat $Q\ns_1$. Since $\RDelta E=0$ for the cycle, a heat $\CQ\ns_2=\CW+Q_1$ must be deposited into the upper reservoir during each cycle. The analog of efficiency here is called the coefficient of refrigeration, $\kappa$, defined as

$$\kappa = {Q\ns_1\over \CW}={Q\ns_1\over \CQ\ns_2-Q\ns_1}\ .$$ Thus, $\kappa$ is proportional to the ratio of the heat extracted to the cost of electricity, per cycle.

[engref] An engine (left) extracts heat $Q_2$ from a reservoir at temperature $T_2$ and deposits a smaller amount of heat $\CQ_1$ into a reservoir at a lower temperature $T_1$, during each cycle. The difference $W=Q_2-\CQ_1$ is transformed into mechanical work. A refrigerator (right) performs the inverse process, drawing heat $Q_1$ from a low temperature reservoir and depositing heat $\CQ_2=Q_1+\CW$ into a high temperature reservoir, where $\CW$ is the mechanical (or electrical) work done per cycle.

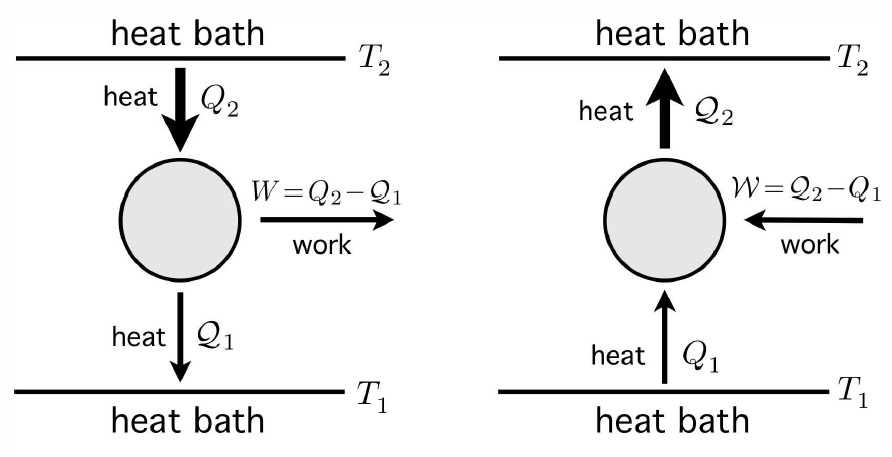
Please note the deliberate notation here. I am using symbols $Q$ and $W$ to denote the heat supplied to the engine (or refrigerator) and the work done by the engine, respectively, and $\CQ$ and $\CW$ to denote the heat taken from the engine and the work done on the engine.

A perfect engine has $\CQ\ns_1=0$ and $\eta=1$; a perfect refrigerator has $Q\ns_1=\CQ\ns_2$ and $\kappa=\infty$. Both violate the Second Law. Sadi Carnot⁸ (1796 – 1832) realized that a reversible cyclic engine operating between two thermal reservoirs must produce the maximum amount of work $W$, and that the amount of work produced is independent of the material properties of the engine. We call any such engine a Carnot engine.

The efficiency of a Carnot engine may be used to define a temperature scale. We know from Carnot’s observations that the efficiency $\eta_\ssr{C}$ can only be a function of the temperatures $T\ns_1$ and $T\ns_2$: $\eta_\ssr{C}=\eta_\ssr{C}(T\ns_1,T\ns_2)$. We can then define

$${T\ns_1\over T\ns_2}\equiv 1-\eta\ns_\ssr{C}(T\ns_1,T\ns_2)\ .$$ Below, in §6.4, we will see that how, using an ideal gas as the ‘working substance’ of the Carnot engine, this temperature scale coincides precisely with the ideal gas temperature scale from §2.4.

Nothing beats a Carnot engine

The Carnot engine is the most efficient engine possible operating between two thermal reservoirs. To see this, let’s suppose that an amazing wonder engine has an efficiency even greater than that of the Carnot engine. A key feature of the Carnot engine is its reversibility – we can just go around its cycle in the opposite direction, creating a Carnot refrigerator. Let’s use our notional wonder engine to drive a Carnot refrigerator, as depicted in Fig. [NBC].

We assume that

$${W\over Q\ns_2} = \eta\ns_\ssr{wonder} > \eta\ns_\ssr{Carnot} = {\CW'\over \CQ'_2}\ .$$ But from the figure, we have $W=\CW'$, and therefore the heat energy $\CQ'_2-Q\ns_2$ transferred to the upper reservoir is positive. From $$W=Q\ns_2-\CQ\ns_1 = \CQ'_2-Q'_1 = \CW'\ ,$$ we see that this is equal to the heat energy extracted from the lower reservoir, since no external work is done on the system: $$\CQ'_2 -Q\ns_2 = Q'_1 -\CQ\ns_1 > 0\ .$$ Therefore, the existence of the wonder engine entails a violation of the Second Law. Since the Second Law is correct – Lord Kelvin articulated it, and who are we to argue with a Lord? – the wonder engine cannot exist.

[NBC] A wonder engine driving a Carnot refrigerator.

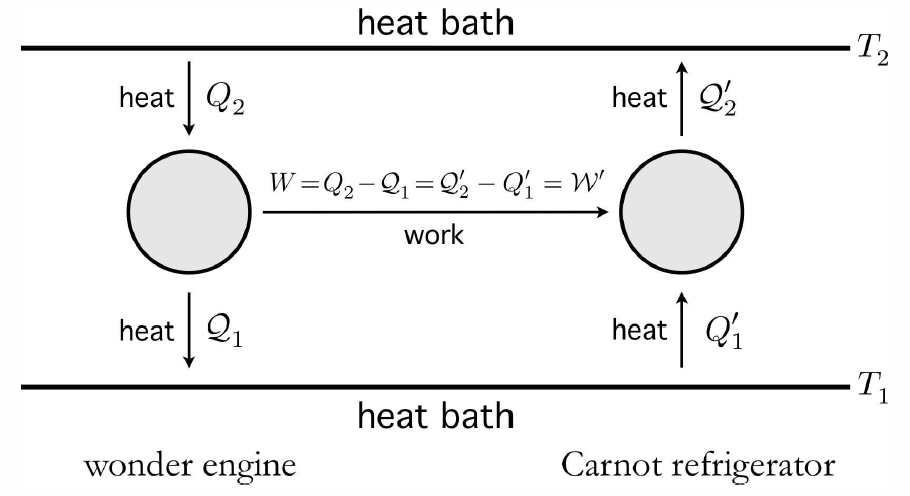
We further conclude that all reversible engines running between two thermal reservoirs have the same efficiency, which is the efficiency of a Carnot engine. For an irreversible engine, we must have

$$\eta={W\over Q\ns_2}=1-{\CQ\ns_1\over Q\ns_2} \le 1-{T\ns_1\over T\ns_2}= \eta\ns_\ssr{C}\ .$$ Thus, $${Q\ns_2\over T\ns_2} - {\CQ\ns_1\over T\ns_1}\le 0\ . \label{qteqn}$$

The Carnot cycle

Let us now consider a specific cycle, known as the Carnot cycle, depicted in Fig. [carnot]. The cycle consists of two adiabats and two isotherms. The work done per cycle is simply the area inside the curve on our $p-V$ diagram:

$$W=\oint \!p\,dV\ .$$ The gas inside our Carnot engine is called the ‘working substance’. Whatever it may be, the system obeys the First Law, $$dE=\dbar Q -\dbar W = \dbar Q - p\,dV \ .$$

We will now assume that the working material is an ideal gas, and we compute $W$ as well as $\CQ\ns_1$ and $Q\ns_2$ to find the efficiency of this cycle. In order to do this, we will rely upon the ideal gas equations,

$$E={\nu R T\over \gamma-1}\qquad,\qquad pV=\nu R T\ ,$$ where $\gamma=c\ns_p/c\ns_v=1+\frac{2}{f}$, where $f$ is the effective number of molecular degrees of freedom contributing to the internal energy. Recall $f=3$ for monatomic gases, $f=5$ for diatomic gases, and $f=6$ for polyatomic gases. The finite difference form of the first law is $$\RDelta E = E\ns_\Rf - E\ns_\Ri = Q\ns_\textsf{if} - W\ns_\textsf{if}\ ,$$ where $\Ri$ denotes the initial state and $\Rf$ the final state.

[carnot] The Carnot cycle consists of two adiabats (dark red) and two isotherms (blue).

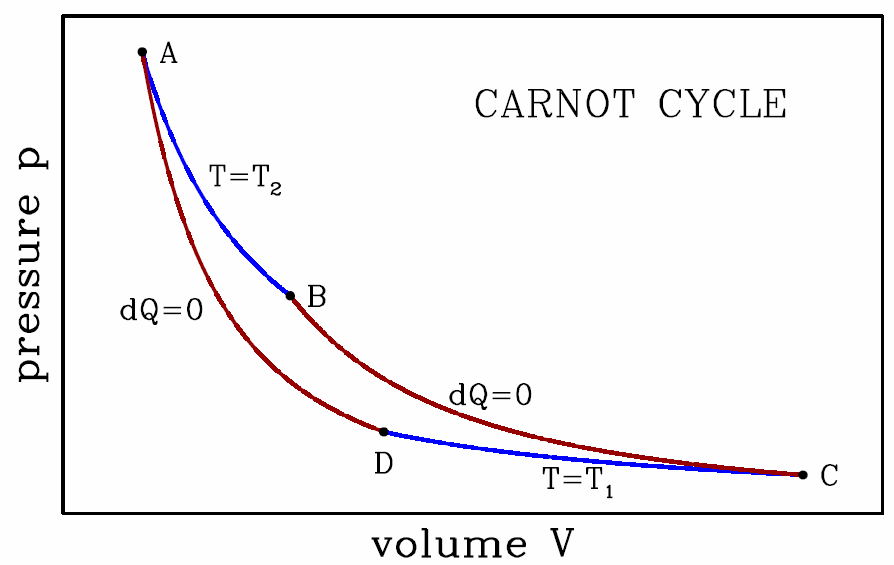
• This stage is an isothermal expansion at temperature $T\ns_2$. It is the ‘power stroke’ of the engine. We have $$\begin{aligned} W\ns_\ssr{AB}&=\int\limits_{V\subA}^{V\subB}\!\!dV\,{\nu R T\ns_2\over V} = \nu R T\ns_2\, \ln\bigg({V\subB\over V\subA}\bigg)\\ E\subA&=E\subB={\nu R T\ns_2\over \gamma-1}\ ,\end{aligned}$$ hence $$Q\ns_\ssr{AB}=\RDelta E\ns_\ssr{AB}+ W\ns_\ssr{AB} = \nu R T\ns_2\,\ln\bigg({V\subB\over V\subA}\bigg)\ .$$
• This stage is an adiabatic expansion. We have $$\begin{aligned} Q\ns_\ssr{BC}&=0\\ \RDelta E\ns_\ssr{BC}&=E\ns_\ssr{C}-E\subB = {\nu R\over \gamma-1}\,(T\ns_1 - T\ns_2)\ .\end{aligned}$$ The energy change is negative, and the heat exchange is zero, so the engine still does some work during this stage: $$W\subBC=Q\ns_\ssr{BC}-\RDelta E\ns_\ssr{BC}= {\nu R\over \gamma-1}\, (T\ns_2 - T\ns_1)\ .$$
• This stage is an isothermal compression, and we may apply the analysis of the isothermal expansion, mutatis mutandis: $$\begin{aligned} W\ns_\ssr{CD}&=\int\limits_{V\ns_\ssr{C}}^{V\ns_\ssr{D}}\!\!dV\,{\nu R T\ns_1\over V} = \nu R T\ns_1\, \ln\bigg({V\ns_\ssr{D}\over V\ns_\ssr{C}}\bigg)\\ E\ns_\ssr{C}&=E\ns_\ssr{D}={\nu R T\ns_1\over \gamma-1}\ ,\end{aligned}$$ hence $$Q\ns_\ssr{CD}=\RDelta E\ns_\ssr{CD}+ W\ns_\ssr{CD} = \nu R T\ns_1\,\ln\bigg({V\ns_\ssr{D}\over V\ns_\ssr{C}}\bigg)\ .$$
• This last stage is an adiabatic compression, and we may draw on the results from the adiabatic expansion in BC: $$\begin{aligned} Q\ns_\ssr{DA}&=0\\ \RDelta E\ns_\ssr{DA}&=E\ns_\ssr{D}-E\subA= {\nu R\over \gamma-1}\,(T\ns_2 - T\ns_1)\ .\end{aligned}$$ The energy change is positive, and the heat exchange is zero, so work is done on the engine: $$W\ns_\ssr{DA}=Q\ns_\ssr{DA}-\RDelta E\ns_\ssr{DA}= {\nu R\over \gamma-1}\,(T\ns_1 - T\ns_2)\ .$$

We now add up all the work values from the individual stages to get for the cycle

$$\begin{split} W&=W\ns_\ssr{AB}+W\ns_\ssr{BC}+W\ns_\ssr{CD}+W\ns_\ssr{DA}\\ &=\nu R T\ns_2\,\ln\bigg({V\subB\over V\subA}\bigg)+\nu R T\ns_1\,\ln\bigg({V\ns_\ssr{D}\over V\ns_\ssr{C}}\bigg)\ . \end{split}$$ Since we are analyzing a cyclic process, we must have $\RDelta E=0$, we must have $Q=W$, which can of course be verified explicitly, by computing $Q=Q\ns_\ssr{AB}+Q\ns_\ssr{BC}+Q\ns_\ssr{CD}+Q\ns_\ssr{DA}$. To finish up, recall the adiabatic ideal gas equation of state, $d(T V^{\gamma-1})=0$. This tells us that $$\begin{aligned} T\ns_2\, V_\ssr{B}^{\gamma-1}&= T\ns_1\, V_\ssr{C}^{\gamma-1} \\ T\ns_2\, V_\ssr{A}^{\gamma-1}&= T\ns_1\, V_\ssr{D}^{\gamma-1} \ .\end{aligned}$$ Dividing these two equations, we find $${V\subB\over V\subA}={V\ns_\ssr{C}\over V\ns_\ssr{D}}\ ,$$ and therefore $$\begin{aligned} W&=\nu R(T\ns_2-T\ns_1)\,\ln\bigg({V\subB\over V\subA}\bigg)\\ Q\ns_\ssr{AB}&=\nu R T\ns_2\,\ln\bigg({V\subB\over V\subA}\bigg)\ .\end{aligned}$$ Finally, the efficiency is given by the ratio of these two quantities: $$\eta={W\over Q\ns_\ssr{AB}}=1-{T\ns_1\over T\ns_2}\ .$$

The Stirling cycle

Many other engine cycles are possible. The Stirling cycle, depicted in Fig. [stirling], consists of two isotherms and two isochores. Recall the isothermal ideal gas equation of state, $d(pV)=0$. Thus, for an ideal gas Stirling cycle, we have

$$p\subA V\ns_1=p\subB V\ns_2 \qquad,\qquad p\ns_\ssr{D} V\ns_1=p\ns_\ssr{C} V\ns_2\ ,$$ which says $${p\subB\over p\subA}={p\subC\over p\subD}={V\ns_1\over V\ns_2}\ .$$

• This isothermal expansion is the power stroke. Assuming $\nu$ moles of ideal gas throughout, we have $pV=\nu R T\ns_2=p\ns_1 V\ns_1$, hence $$W\subAB=\int\limits_{V\ns_1}^{V\ns_2}\!\!dV\,{\nu R T\ns_2\over V}=\nu R T\ns_2\,\ln\bigg({V\ns_2\over V\ns_1}\bigg)\ .$$ Since AB is an isotherm, we have $E\subA=E\subB$, and from $\RDelta E\subAB=0$ we conclude $Q\subAB=W\subAB$.
• Isochoric cooling. Since $dV=0$ we have $W\subBC=0$. The energy change is given by $$\RDelta E\subBC=E\subC-E\subB={\nu R(T\ns_1-T\ns_2)\over\gamma-1} ,$$ which is negative. Since $W\subBC=0$, we have $Q\subBC=\RDelta E\subBC$.

[stirling] A Stirling cycle consists of two isotherms (blue) and two isochores (green).

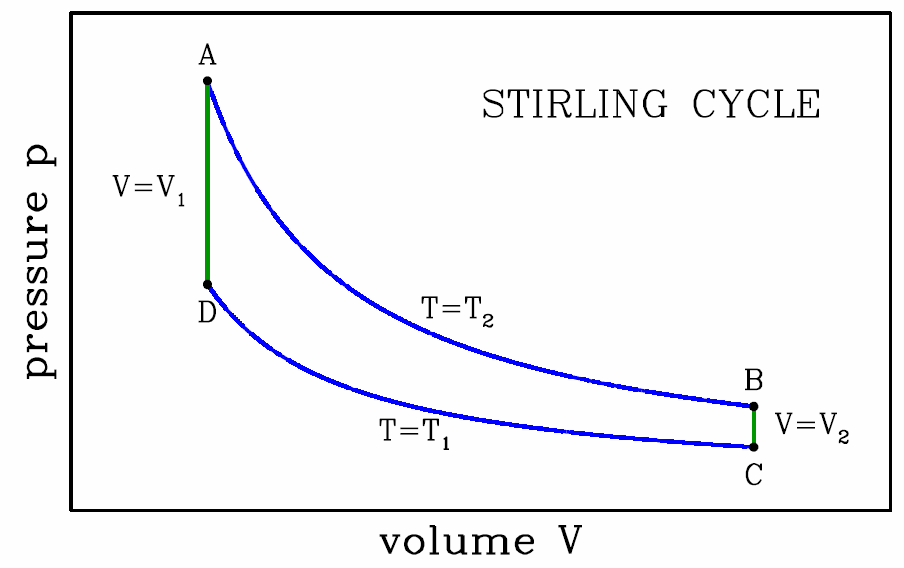
• Isothermal compression. Clearly $$W\subCD=\int\limits_{V\ns_2}^{V\ns_1}\!\!dV\,{\nu R T\ns_1\over V}= -\nu R T\ns_1\,\ln\bigg({V\ns_2\over V\ns_1}\bigg)\ .$$ Since CD is an isotherm, we have $E\subC=E\subD$, and from $\RDelta E\subCD=0$ we conclude $Q\subCD=W\subCD$.
• Isochoric heating. Since $dV=0$ we have $W\subDA=0$. The energy change is given by $$\RDelta E\subDA=E\subA-E\subD={\nu R(T\ns_2-T\ns_1)\over\gamma-1}\ ,$$ which is positive, and opposite to $\RDelta E\subBC$. Since $W\subDA=0$, we have $Q\subDA=\RDelta E\subDA$.

We now add up all the work contributions to obtain

$$\begin{split} W&=W\ns_\ssr{AB}+W\ns_\ssr{BC}+W\ns_\ssr{CD}+W\ns_\ssr{DA}\\ &=\nu R (T\ns_2-T\ns_1)\,\ln\bigg({V\ns_2\over V\ns_1}\bigg)\ . \end{split}$$ The cycle efficiency is once again $$\eta={W\over Q\subAB}=1-{T\ns_1\over T\ns_2}\ .$$

The Otto and Diesel cycles

The Otto cycle is a rough approximation to the physics of a gasoline engine. It consists of two adiabats and two isochores, and is depicted in Fig. [otto]. Assuming an ideal gas, along the adiabats we have $d(pV^\gamma)=0$. Thus,

$$p\subA\,V^\gamma_1=p\subB\,V^\gamma_2 \qquad,\qquad p\ns_\ssr{D}\,V^\gamma_1=p\ns_\ssr{C}\,V^\gamma_2\ ,$$ which says $${p\subB\over p\subA}={p\subC\over p\subD}= \bigg({V\ns_1\over V\ns_2}\bigg)^{\!\gamma}\ .$$

[otto] An Otto cycle consists of two adiabats (dark red) and two isochores (green).

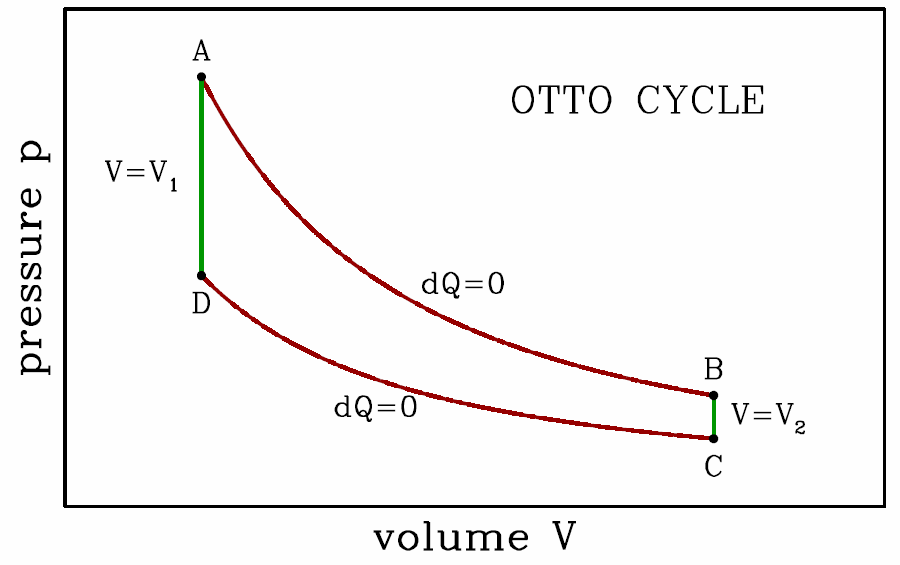
• Adiabatic expansion, the power stroke. The heat transfer is $Q\subAB=0$, so from the First Law we have $W\subAB=-\RDelta E\subAB=E\subA-E\subB$, thus $$W\subAB={p\subA V\ns_1-p\subB V\ns_2\over\gamma-1} ={p\subA V\ns_1\over \gamma-1}\Bigg[ 1-\bigg({V\ns_1\over V\ns_2}\bigg)^{\!\gamma-1} \Bigg]\ .$$ Note that this result can also be obtained from the adiabatic equation of state $pV^\gamma=p\subA V_1^\gamma$: $$W\subAB=\int\limits_{V\ns_1}^{V\ns_2}\!\!p\,dV= p\subA V_1^\gamma\!\int\limits_{V\ns_1}^{V\ns_2}\!dV\,V^{-\gamma} ={p\subA V\ns_1\over \gamma-1}\Bigg[ 1-\bigg({V\ns_1\over V\ns_2}\bigg)^{\!\gamma-1} \Bigg]\ .$$
• Isochoric cooling (exhaust); $dV=0$ hence $W\subBC=0$. The heat $Q\subBC$ absorbed is then $$Q\subBC=E\subC-E\subB={V\ns_2\over\gamma-1}\,(p\subC-p\subB)\ .$$ In a realistic engine, this is the stage in which the old burned gas is ejected and new gas is inserted.

• Adiabatic compression; $Q\subCD=0$ and $W\subCD=E\subC-E\subD$: $$W\subCD={p\subC V\ns_2 - p\subD V\ns_1\over \gamma-1} =-{p\subD V\ns_1\over \gamma-1}\Bigg[ 1-\bigg({V\ns_1\over V\ns_2}\bigg)^{\!\gamma-1} \Bigg]\ .$$
• Isochoric heating, the combustion of the gas. As with BC we have $dV=0$, and thus $W\subDA=0$. The heat $Q\subDA$ absorbed by the gas is then $$Q\subDA=E\subA-E\subD={V\ns_1\over\gamma-1}\,(p\subA-p\subD)\ .$$

[diesel] A Diesel cycle consists of two adiabats (dark red), one isobar (light blue), and one isochore (green).

The total work done per cycle is then

$$\begin{split} W&=W\ns_\ssr{AB}+W\ns_\ssr{BC}+W\ns_\ssr{CD}+W\ns_\ssr{DA}\\ &={(p\subA-p\subD)V\ns_1\over\gamma-1} \Bigg[ 1-\bigg({V\ns_1\over V\ns_2}\bigg)^{\!\gamma-1}\Bigg]\ , \end{split}$$ and the efficiency is defined to be $$\eta\equiv{W\over Q\subDA}=1-\bigg({V\ns_1\over V\ns_2}\bigg)^{\!\gamma-1}\ .$$ The ratio $V\ns_2/V\ns_1$ is called the compression ratio. We can make our Otto cycle more efficient simply by increasing the compression ratio. The problem with this scheme is that if the fuel mixture becomes too hot, it will spontaneously ‘preignite’, and the pressure will jump up before point D in the cycle is reached. A Diesel engine avoids preignition by compressing the air only, and then later spraying the fuel into the cylinder when the air temperature is sufficient for fuel ignition. The rate at which fuel is injected is adjusted so that the ignition process takes place at constant pressure. Thus, in a Diesel engine, step DA is an isobar. The compression ratio is $r\equiv V\subB/V\subD$, and the cutoff ratio is $s\equiv V\subA/V\subD$. This refinement of the Otto cycle allows for higher compression ratios (of about 20) in practice, and greater engine efficiency.

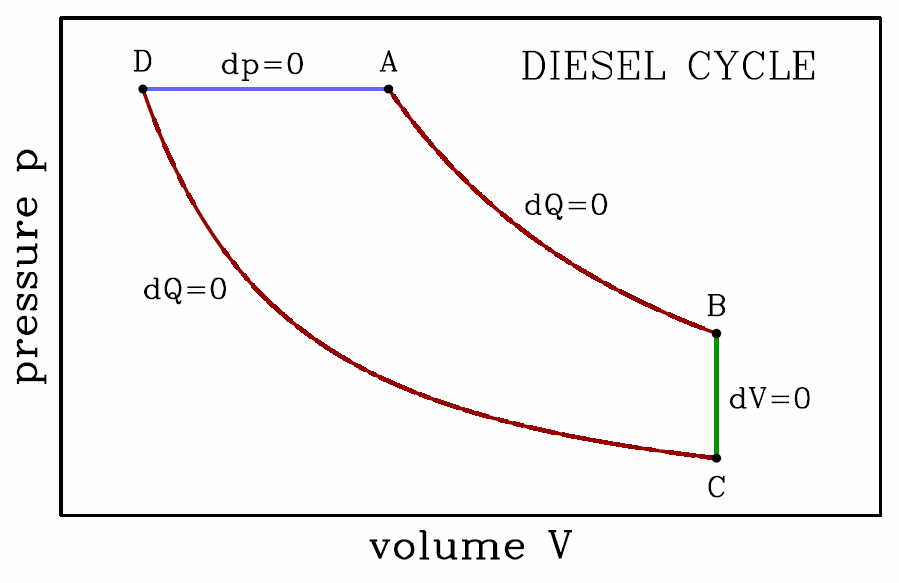
For the Diesel cycle, we have, briefly,

$$\begin{split} W&=p\subA(V\subA-V\subD) + {p\subA V\subA-p\subB V\subB\over\gamma-1} + {p\subC V\subC-p\subD V\subD\over\gamma-1}\\ &={\gamma\,p\subA(V\subA-V\subD)\over\gamma-1} - {(p\subB-p\subC) V\subB\over\gamma-1} \end{split}$$ and $$Q\subDA={\gamma\,p\subA(V\subA-V\subD)\over\gamma-1}\ .$$ To find the efficiency, we will need to eliminate $p\subB$ and $p\subC$ in favor of $p\subA$ using the adiabatic equation of state $d(pV^\gamma)=0$. Thus, $$p\subB=p\subA\cdot\bigg({V\subA\over V\subB}\bigg)^{\!\!\gamma}\qquad,\qquad p\subC=p\subA\cdot\bigg({V\subD\over V\subB}\bigg)^{\!\!\gamma}\ ,$$ where we’ve used $p\subD=p\subA$ and $V\subC=V\subB$. Putting it all together, the efficiency of the Diesel cycle is $$\eta={W\over Q\subDA}=1-{1\over\gamma}\,{r^{1-\gamma} (s^\gamma-1)\over s-1}\ .$$

The Joule-Brayton cycle

Our final example is the Joule-Brayton cycle, depicted in Fig. [jbray], consisting of two adiabats and two isobars. Along the adiabats we have Thus,

$$p\ns_2\,V^\gamma_\ssr{A}=p\ns_1\,V^\gamma_\ssr{D} \qquad,\qquad p\ns_2\,V^\gamma_\ssr{B}=p\ns_1\,V^\gamma_\ssr{C}\ ,$$ which says $${V\subD\over V\subA}={V\subC\over V\subB}= \bigg({p\ns_2\over p\ns_1}\bigg)^{\!\gamma^{-1}}\ .$$

• This isobaric expansion at $p=p\ns_2$ is the power stroke. We have $$\begin{aligned} W\subAB&=\int\limits_{V\subA}^{V\subB}\!\!dV\,p\ns_2 = p\ns_2\,(V\subB-V\subA)\\ \RDelta E\subAB&=E\subB-E\subA={p\ns_2\,(V\subB-V\subA)\over\gamma-1}\\ Q\subAB&=\RDelta E\subAB + W\subAB= {\gamma \,p\ns_2\,(V\subB-V\subA)\over\gamma-1}\ .\end{aligned}$$
• Adiabatic expansion; $Q\subBC=0$ and $W\subBC=E\subB-E\subC$. The work done by the gas is $$\begin{split} W\subBC&={p\ns_2 V\subB-p\ns_1 V\subC\over\gamma-1}= {p\ns_2 V\subB\over\gamma-1}\bigg(1-{p\ns_1\over p\ns_2} \cdot{V\subC\over V\subB}\bigg)\\ &={p\ns_2\, V\subB\over \gamma-1}\Bigg[ 1-\bigg({p\ns_1\over p\ns_2} \bigg)^{\!1-\gamma^{-1}}\Bigg]\ . \end{split}$$

[jbray] A Joule-Brayton cycle consists of two adiabats (dark red) and two isobars (light blue).

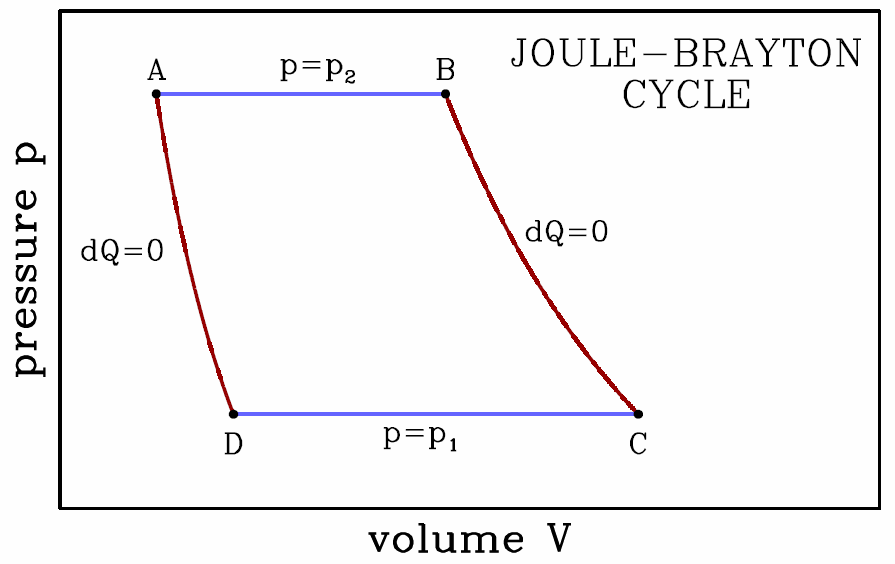
• Isobaric compression at $p=p\ns_1$. $$\begin{aligned} W\subCD&=\int\limits_{V\subC}^{V\subD}\!\!dV\,p\ns_1 = p\ns_1\,(V\subD-V\subC) =-p\ns_2\,(V\subB-V\subA)\,\bigg({p\ns_1\over p\ns_2}\bigg)^{\!1-\gamma^{-1}}\\ \RDelta E\subCD&=E\subD-E\subC={p\ns_1\,(V\subD-V\subC)\over\gamma-1}\\ Q\subCD&=\RDelta E\subCD + W\subCD= -{\gamma \,p\ns_2\over\gamma-1}\,(V\subB-V\subA)\,\bigg({p\ns_1\over p\ns_2} \bigg)^{\!1-\gamma^{-1}}\ .\end{aligned}$$
• Adiabatic expansion; $Q\subDA=0$ and $W\subDA=E\subD-E\subA$. The work done by the gas is $$\begin{split} W\subDA&={p\ns_1 V\subD-p\ns_2 V\subA\over\gamma-1}= -{p\ns_2 V\subA\over\gamma-1}\bigg(1-{p\ns_1\over p\ns_2} \cdot{V\subD\over V\subA}\bigg)\\ &=-{p\ns_2\, V\subA\over \gamma-1}\Bigg[ 1-\bigg({p\ns_1\over p\ns_2} \bigg)^{\!1-\gamma^{-1}}\Bigg]\ . \end{split}$$

The total work done per cycle is then

$$\begin{split} W&=W\ns_\ssr{AB}+W\ns_\ssr{BC}+W\ns_\ssr{CD}+W\ns_\ssr{DA}\\ &={\gamma\,p\ns_2\, (V\subB-V\subA)\over \gamma-1}\Bigg[ 1-\bigg({p\ns_1\over p\ns_2} \bigg)^{\!1-\gamma^{-1}}\Bigg] \end{split}$$ and the efficiency is defined to be $$\eta\equiv{W\over Q\subAB}=1-\bigg({p\ns_1\over p\ns_2}\bigg)^{\!1-\gamma^{-1}}\ .$$

Carnot engine at maximum power output

While the Carnot engine described above in §6.4 has maximum efficiency, it is practically useless, because the isothermal processes must take place infinitely slowly in order for the working material to remain in thermal equilibrium with each reservoir. Thus, while the work done per cycle is finite, the cycle period is infinite, and the engine power is zero.

A modification of the ideal Carnot cycle is necessary to create a practical engine. The idea⁹ is as follows. During the isothermal expansion stage, the working material is maintained at a temperature $T\ns_{2\Rw}<T\ns_2$. The temperature difference between the working material and the hot reservoir drives a thermal current,

$${\dbar Q\ns_2\over dt}=\kappa\ns_2\,(T\ns_2-T\ns_{2\Rw})\ .$$ Here, $\kappa\ns_2$ is a transport coefficient which describes the thermal conductivity of the chamber walls, multiplied by a geometric parameter (which is the ratio of the total wall area to its thickness). Similarly, during the isothermal compression, the working material is maintained at a temperature $T\ns_{1\Rw}>T\ns_1$, which drives a thermal current to the cold reservoir, $${\dbar\CQ\ns_1\over dt}=\kappa\ns_1\,(T\ns_{1\Rw}-T\ns_1)\ .$$ Now let us assume that the upper isothermal stage requires a duration $\RDelta t\ns_2$ and the lower isotherm a duration $\RDelta t\ns_1$. Then $$\begin{aligned} Q\ns_2&=\kappa\ns_2\,\RDelta t\nd_2\,(T\ns_2-T\ns_{2\Rw})\\ \CQ\ns_1&=\kappa\ns_1\,\RDelta t\nd_1\,(T\ns_{1\Rw}-T\ns_1)\ .\end{aligned}$$ Since the engine is reversible, we must have $${\CQ\ns_1\over T\ns_{1\Rw}}={Q\ns_2\over T\ns_{2\Rw}}\ ,$$ which says $${\RDelta t\ns_1\over\RDelta t\ns_2}={\kappa\ns_2\,T\ns_{1\Rw}\,(T\ns_2-T\ns_{2\Rw}) \over \kappa\ns_1\,T\ns_{2\Rw}\,(T\ns_{1\Rw}-T\ns_1)}\ .$$ The power is $$P={Q\ns_2-\CQ\ns_1\over (1+\alpha)\,(\RDelta t\ns_1 + \RDelta t\ns_2)}\ ,$$ where we assume that the adiabatic stages require a combined time of $\alpha\,(\RDelta t\ns_1 + \RDelta t\ns_2)$. Thus, we find $$P={\kappa\ns_1\,\kappa\ns_2\over 1+\alpha}\cdot{(T\ns_{2\Rw}-T\ns_{1\Rw})\,(T\ns_{1\Rw}-T\ns_1) \,(T\ns_2-T\ns_{2\Rw})\over \kappa\ns_1\,T\ns_{2\Rw}\,(T\ns_{1\Rw}-T\ns_1) +\kappa\ns_2\,T\ns_{1\Rw}\,(T\ns_2-T\ns_{2\Rw})}$$

[pptab] Observed performances of real heat engines, taken from table 1 from Curzon and Albhorn (1975).

Power source	$T\ns_1\ ({}^\circ\RC)$	$T\ns_2\ ({}^\circ\RC)$	$\eta\ns_\ssr{Carnot}$	$\eta$ (theor.)	$\eta$ (obs.)
West Thurrock (UK)
Coal Fired Steam Plant	$\sim 25$	$565$	$0.641$	$0.40$	$0.36$
CANDU (Canada)
PHW Nuclear Reactor	$\sim 25$	$300$	$0.480$	$0.28$	$0.30$
Larderello (Italy)
Geothermal Steam Plant	$\sim 80$	$250$	$0.323$	$0.175$	$0.16$

We optimize the engine by maximizing $P$ with respect to the temperatures $T\ns_{1\Rw}$ and $T\ns_{2\Rw}$. This yields

$$\begin{aligned} T\ns_{2\Rw}&=T\ns_2-{T\ns_2-\sqrt{T\ns_1 T\ns_2}\over 1+\sqrt{\kappa\ns_2/\kappa\ns_1}}\\ T\ns_{1\Rw}&=T\ns_1+{\sqrt{T\ns_1 T\ns_2}-T\ns_1\over 1+\sqrt{\kappa\ns_1/\kappa\ns_2}}\ .\end{aligned}$$ The efficiency at maximum power is then \[\eta={Q\ns_2-\CQ\ns_1\over Q\ns_2}=1-{T\ns_{1\Rw}\over T\ns_{2\Rw}}= 1-\sqrt

ParseError: EOF expected (click for details)

Callstack:
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/div[8]/p[3]/span[1], line 1, column 2

\ . \label{MCeff}\] One also finds at maximum power \[{\RDelta t\ns_2\over \RDelta t\ns_1}=\sqrt

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.05:_Heat_Engines_and_the_Second_Law_of_Thermodynamics), /content/body/div[8]/p[3]/span[2], line 1, column 1

\ .\] Finally, the maximized power is $$P\ns_{max}={\kappa\ns_1\kappa\ns_2\over 1+\alpha}\,\Bigg({\sqrt{T\ns_2}-\sqrt{T\ns_1} \over\sqrt{\kappa\ns_1}+\sqrt{\kappa\ns_2}}\Bigg)^{\!2}\ .$$

Table [pptab], taken from the article of Curzon and Albhorn (1975), shows how the efficiency of this practical Carnot cycle, given by Equation [MCeff], rather accurately predicts the efficiencies of functioning power plants.