3.2: Phase Flows in Classical Mechanics

$\newcommand\bes{\begin{equation}\begin{split}}$
$\newcommand\ltwid{\propto}$
$\newcommand\ees{\end{split}\end{equation}}$
$\newcommand\mib{\mathbf}$
$\newcommand\Sa{\textsf a}$
$\newcommand\Sb{\textsf b}$
$\newcommand\Sc{\textsf c}$
$\newcommand\Sd{\textsf d}$
$\newcommand\Se{\textsf e}$
$\newcommand\Sf{\textsf f}$
$\newcommand\Sg{\textsf g}$
$\newcommand\Sh{\textsf h}$
$\newcommand\Si{\textsf i}$
$\newcommand\Sj{\textsf j}$
$\newcommand\Sk{\textsf k}$
$\newcommand\Sl{\textsf l}$
$\newcommand\Sm{\textsf m}$
$\newcommand\Sn{\textsf n}$
$\newcommand\So{\textsf o}$
$\newcommand\Sp{\textsf p}$
$\newcommand\Sq{\textsf q}$
$\newcommand\Sr{\textsf r}$
$\newcommand\Ss{\textsf s}$
$\newcommand\St{\textsf t}$
$\newcommand\Su{\textsf u}$
$\newcommand\Sv{\textsf v}$
$\newcommand\Sw{\textsf w}$
$\newcommand\Sx{\textsf x}$
$\newcommand\Sy{\textsf y}$
$\newcommand\Sz{\textsf z}$
$\newcommand\SA{\textsf A}$
$\newcommand\SB{\textsf B}$
$\newcommand\SC{\textsf C}$
$\newcommand\SD{\textsf D}$
$\newcommand\SE{\textsf E}$
$\newcommand\SF{\textsf F}$
$\newcommand\SG{\textsf G}$
$\newcommand\SH{\textsf H}$
$\newcommand\SI{\textsf I}$
$\newcommand\SJ{\textsf J}$
$\newcommand\SK{\textsf K}$
$\newcommand\SL{\textsf L}$
$\newcommand\SM{\textsf M}$
$\newcommand\SN{\textsf N}$
$\newcommand\SO{\textsf O}$
$\newcommand\SP{\textsf P}$
$\newcommand\SQ{\textsf Q}$
$\newcommand\SR{\textsf R}$
$\newcommand\SS{\textsf S}$
$\newcommand\ST{\textsf T}$
$\newcommand\SU{\textsf U}$
$\newcommand\SV{\textsf V}$
$\newcommand\SW{\textsf W}$
$\newcommand\SX{\textsf X}$
$\newcommand\SY{\textsf Y}$
$\newcommand\SZ{\textsf Z}$
$\newcommand\Ha{\hat a}$
$\newcommand\Hb{\hat b}$
$\newcommand\Hc{\hat c}$
$\newcommand\Hd{\hat d}$
$\newcommand\He{\hat e}$
$\newcommand\Hf{\hat f}$
$\newcommand\Hg{\hat g}$
$\newcommand\Hh{\hat h}$
$\newcommand\Hi{\hat \imath}$
$\newcommand\Hj{\hat \jmath}$
$\newcommand\Hk{\hat k}$
$\newcommand\Hl{\hat l}$
$\newcommand\Hm{\hat m}$
$\newcommand\Hn{\hat n}$
$\newcommand\Ho{\hat o}$
$\newcommand\Hp{\hat p}$
$\newcommand\Hq{\hat q}$
$\newcommand\Hr{\hat r}$
$\newcommand\Hs{\hat s}$
$\newcommand\Ht{\hat t}$
$\newcommand\Hu{\hat u}$
$\newcommand\Hv{\hat v}$
$\newcommand\Hw{\hat w}$
$\newcommand\Hx{\hat x}$
$\newcommand\Hy{\hat y}$
$\newcommand\Hz{\hat z}$
$\newcommand\HA{\hat A}$
$\newcommand\HB{\hat B}$
$\newcommand\HC{\hat C}$
$\newcommand\HD{\hat D}$
$\newcommand\HE{\hat E}$
$\newcommand\HF{\hat F}$
$\newcommand\HG{\hat G}$
$\newcommand\HH{\hat H}$
$\newcommand\HI{\hat I}$
$\newcommand\HJ{\hat J}$
$\newcommand\HK{\hat K}$
$\newcommand\HL{\hat L}$
$\newcommand\HM{\hat M}$
$\newcommand\HN{\hat N}$
$\newcommand\HO{\hat O}$
$\newcommand\HP{\hat P}$
$\newcommand\HQ{\hat Q}$
$\newcommand\HR{\hat R}$
$\newcommand\HS{\hat S}$
$\newcommand\HT{\hat T}$
$\newcommand\HU{\hat U}$
$\newcommand\HV{\hat V}$
$\newcommand\HW{\hat W}$
$\newcommand\HX{\hat X}$
$\newcommand\HY{\hat Y}$
$\newcommand\HZ{\hat Z}$
$\newcommand\Halpha{\hat\alpha}$
$\newcommand\Hbeta{\hat\beta}$
$\newcommand\Hgamma{\hat\gamma}$
$\newcommand\Hdelta{\hat\delta}$
$\newcommand\Hepsilon{\hat\epsilon}$
$\newcommand\Hvarepsilon{\hat\varepsilon}$
$\newcommand\Hzeta{\hat\zeta}$
$\newcommand\Heta{\hat\eta}$
$\newcommand\Htheta{\hat\theta}$
$\newcommand\Hvartheta{\hat\vartheta}$
$\newcommand\Hiota{\hat\iota}$
$\newcommand\Hkappa{\hat\kappa}$
$\newcommand\Hlambda{\hat\lambda}$
$\newcommand\Hmu{\hat\mu}$
$\newcommand\Hnu{\hat\nu}$
$\newcommand\Hxi{\hat\xi}$
$\newcommand\Hom{\hat\omicron}$
$\newcommand\Hpi{\hat\pi}$
$\newcommand\Hvarpi{\hat\varpi}$
$\newcommand\Hrho{\hat\rho}$
$\newcommand\Hvarrho{\hat\varrho}$
$\newcommand\Hsigma{\hat\sigma}$
$\newcommand\Hvarsigma{\hat\varsigma}$
$\newcommand\Htau{\var\tau}$
$\newcommand\Hupsilon{\hat\upsilon}$
$\newcommand\Hphi{\hat\phi}$
$\newcommand\Hvarphi{\hat\varphi}$
$\newcommand\Hchi{\hat\chi}$
$\newcommand\Hxhi{\hat\xhi}$
$\newcommand\Hpsi{\hat\psi}$
$\newcommand\Homega{\hat\omega}$
$\newcommand\HGamma{\hat\Gamma}$
$\newcommand\HDelta{\hat\Delta}$
$\newcommand\HTheta{\hat\Theta}$
$\newcommand\HLambda{\hat\Lambda}$
$\newcommand\HXi{\hat\Xi}$
$\newcommand\HPi{\hat\Pi}$
$\newcommand\HSigma{\hat\Sigma}$
$\newcommand\HUps{\hat\Upsilon}$
$\newcommand\HPhi{\hat\Phi}$
$\newcommand\HPsi{\hat\Psi}$
$\newcommand\HOmega{\hat\Omega}$
$\newcommand\xhat{\hat\Bx}$
$\newcommand\yhat{\hat\By}$
$\newcommand\zhat{\hat\Bz}$
$\newcommand\ehat{\hat\Be}$
$\newcommand\khat{\hat\Bk}$
$\newcommand\nhat{\hat\Bn}$
$\newcommand\rhat{\hat\Br}$
$\newcommand\phihat{\hat\Bphi}$
$\newcommand\thetahat{\hat\Btheta}$
$\newcommand\MA{\mathbb A}$
$\newcommand\MB{\mathbb B}$
$\newcommand\MC{\mathbb C}$
$\newcommand\MD{\mathbb D}$
$\newcommand\ME{\mathbb E}$
$\newcommand\MF{\mathbb F}$
$\newcommand\MG{\mathbb G}$
$\newcommand\MH{\mathbb H}$
$\newcommand\MI{\mathbb I}$
$\newcommand\MJ{\mathbb J}$
$\newcommand\MK{\mathbb K}$
$\newcommand\ML{\mathbb L}$
$\newcommand\MM{\mathbb M}$
$\newcommand\MN{\mathbb N}$
$\newcommand\MO{\mathbb O}$
$\newcommand\MP{\mathbb P}$
$\newcommand\MQ{\mathbb Q}$
$\newcommand\MR{\mathbb R}$
$\newcommand\MS{\mathbb S}$
$\newcommand\MT{\mathbb T}$
$\newcommand\MU{\mathbb U}$
$\newcommand\MV{\mathbb V}$
$\newcommand\MW{\mathbb W}$
$\newcommand\MX{\mathbb X}$
$\newcommand\MY{\mathbb Y}$
$\newcommand\MZ{\mathbb Z}$
$\newcommand\CA{\mathcal A}$
$\newcommand\CB{\mathcal B}$
$\newcommand\CC{\mathcal C}$
$\newcommand\CD{\mathcal D}$
$\newcommand\CE{\mathcal E}$
$\newcommand\CF{\mathcal F}$
$\newcommand\CG{\mathcal G}$
$\newcommand\CH{\mathcal H}$
$\newcommand\CI{\mathcal I}$
$\newcommand\CJ{\mathcal J}$
$\newcommand\CK{\mathcal K}$
$\newcommand\CL{\mathcal L}$
$\newcommand\CM{\mathcal M}$
$\newcommand\CN{\mathcal N}$
$\newcommand\CO{\mathcal O}$
$\newcommand\CP{\mathcal P}$
$\newcommand\CQ{\mathcal Q}$
$\newcommand\CR{\mathcal R}$
$\newcommand\CS{\mathcal S}$
$\newcommand\CT{\mathcal T}$
$\newcommand\CU{\mathcal U}$
$\newcommand\CV{\mathcal V}$
$\newcommand\CW{\mathcal W}$
$\newcommand\CX{\mathcal X}$
$\newcommand\CY{\mathcal Y}$
$\newcommand\CZ{\mathcal Z}$
$\newcommand\Fa{\mathfrak a}$
$\newcommand\Fb{\mathfrak b}$
$\newcommand\Fc{\mathfrak c}$
$\newcommand\Fd{\mathfrak d}$
$\newcommand\Fe{\mathfrak e}$
$\newcommand\Ff{\mathfrak f}$
$\newcommand\Fg{\mathfrak g}$
$\newcommand\Fh{\mathfrak h}$
$\newcommand\Fi{\mathfrak i}$
$\newcommand\Fj{\mathfrak j}$
$\newcommand\Fk{\mathfrak k}$
$\newcommand\Fl{\mathfrak l}$
$\newcommand\Fm{\mathfrak m}$
$\newcommand\Fn{\mathfrak n}$
$\newcommand\Fo{\mathfrak o}$
$\newcommand\Fp{\mathfrak p}$
$\newcommand\Fq{\mathfrak q}$
$\newcommand\Fr{\mathfrak r}$
$\newcommand\Fs{\mathfrak s}$
$\newcommand\Ft{\mathfrak t}$
$\newcommand\Fu{\mathfrak u}$
$\newcommand\Fv{\mathfrak v}$
$\newcommand\Fw{\mathfrak w}$
$\newcommand\Fx{\mathfrak x}$
$\newcommand\Fy{\mathfrak y}$
$\newcommand\Fz{\mathfrak z}$
$\newcommand\FA{\mathfrak A}$
$\newcommand\FB{\mathfrak B}$
$\newcommand\FC{\mathfrak C}$
$\newcommand\FD{\mathfrak D}$
$\newcommand\FE{\mathfrak E}$
$\newcommand\FF{\mathfrak F}$
$\newcommand\FG{\mathfrak G}$
$\newcommand\FH{\mathfrak H}$
$\newcommand\FI{\mathfrak I}$
$\newcommand\FJ{\mathfrak J}$
$\newcommand\FK{\mathfrak K}$
$\newcommand\FL{\mathfrak L}$
$\newcommand\FM{\mathfrak M}$
$\newcommand\FN{\mathfrak N}$
$\newcommand\FO{\mathfrak O}$
$\newcommand\FP{\mathfrak P}$
$\newcommand\FQ{\mathfrak Q}$
$\newcommand\FR{\mathfrak R}$
$\newcommand\FS{\mathfrak S}$
$\newcommand\FT{\mathfrak T}$
$\newcommand\FU{\mathfrak U}$
$\newcommand\FV{\mathfrak V}$
$\newcommand\FW{\mathfrak W}$
$\newcommand\FX{\mathfrak X}$
$\newcommand\FY{\mathfrak Y}$
$\newcommand\FZ{\mathfrak Z}$
$\newcommand\Da{\dot a}$
$\newcommand\Db{\dot b}$
$\newcommand\Dc{\dot c}$
$\newcommand\Dd{\dot d}$
$\newcommand\De{\dot e}$
$\newcommand\Df{\dot f}$
$\newcommand\Dg{\dot g}$
$\newcommand\Dh{\dot h}$
$\newcommand\Di{\dot \imath}$
$\newcommand\Dj{\dot \jmath}$
$\newcommand\Dk{\dot k}$
$\newcommand\Dl{\dot l}$
$\newcommand\Dm{\dot m}$
$\newcommand\Dn{\dot n}$
$\newcommand\Do{\dot o}$
$\newcommand\Dp{\dot p}$
$\newcommand\Dq{\dot q}$
$\newcommand\Dr{\dot r}$
$\newcommand\Ds{\dot s}$
$\newcommand\Dt{\dot t}$
$\newcommand\Du{\dot u}$
$\newcommand\Dv{\dot v}$
$\newcommand\Dw{\dot w}$
$\newcommand\Dx{\dot x}$
$\newcommand\Dy{\dot y}$
$\newcommand\Dz{\dot z}$
$\newcommand\DA{\dot A}$
$\newcommand\DB{\dot B}$
$\newcommand\DC{\dot C}$
$\newcommand\DD{\dot D}$
$\newcommand\DE{\dot E}$
$\newcommand\DF{\dot F}$
$\newcommand\DG{\dot G}$
$\newcommand\DH{\dot H}$
$\newcommand\DI{\dot I}$
$\newcommand\DJ{\dot J}$
$\newcommand\DK{\dot K}$
$\newcommand\DL{\dot L}$
$\newcommand\DM{\dot M}$
$\newcommand\DN{\dot N}$
$\newcommand\DO{\dot O}$
$\newcommand\DP{\dot P}$
$\newcommand\DQ{\dot Q}$
$\newcommand\DR{\dot R}$
$\newcommand\DS{\dot S}$
$\newcommand\DT{\dot T}$
$\newcommand\DU{\dot U}$
$\newcommand\DV{\dot V}$
$\newcommand\DW{\dot W}$
$\newcommand\DX{\dot X}$
$\newcommand\DY{\dot Y}$
$\newcommand\DZ{\dot Z}$
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
$\newcommand\Dmu{\dot\mu}$
$\newcommand\Dnu{\dot\nu}$
$\newcommand\Dxi{\dot\xi}$
$\newcommand\Dom{\dot\omicron}$
$\newcommand\Dpi{\dot\pi}$
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
$\newcommand\Drho{\dot\rho}$
$\newcommand\Dvarrho{\dot\varrho}$
$\newcommand\Dsigma{\dot\sigma}$
$\newcommand\Dvarsigma{\dot\varsigma}$
$\newcommand\Dtau{\var\tau}$
$\newcommand\Dupsilon{\dot\upsilon}$
$\newcommand\Dphi{\dot\phi}$
$\newcommand\Dvarphi{\dot\varphi}$
$\newcommand\Dchi{\dot\chi}$
$\newcommand\Dpsi{\dot\psi}$
$\newcommand\Domega{\dot\omega}$
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
$\newcommand\DLambda{\dot\Lambda}$
$\newcommand\DXi{\dot\Xi}$
$\newcommand\DPi{\dot\Pi}$
$\newcommand\DSigma{\dot\Sigma}$
$\newcommand\DUps{\dot\Upsilon}$
$\newcommand\DPhi{\dot\Phi}$
$\newcommand\DPsi{\dot\Psi}$
$\newcommand\DOmega{\dot\Omega}$
$\newcommand\Va{\vec a}$
$\newcommand\Vb{\vec b}$
$\newcommand\Vc{\vec c}$
$\newcommand\Vd{\vec d}$
$\newcommand\Ve{\vec e}$
$\newcommand\Vf{\vec f}$
$\newcommand\Vg{\vec g}$
$\newcommand\Vh{\vec h}$
$\newcommand\Vi{\vec \imath}$
$\newcommand\Vj{\vec \jmath}$
$\newcommand\Vk{\vec k}$
$\newcommand\Vl{\vec l}$
$\newcommand\Vm{\vec m}$
$\newcommand\Vn{\vec n}$
$\newcommand\Vo{\vec o}$
$\newcommand\Vp{\vec p}$
$\newcommand\Vq{\vec q}$
$\newcommand\Vr{\vec r}$
$\newcommand\Vs{\vec s}$
$\newcommand\Vt{\vec t}$
$\newcommand\Vu{\vec u}$
$\newcommand\Vv{\vec v}$
$\newcommand\Vw{\vec w}$
$\newcommand\Vx{\vec x}$
$\newcommand\Vy{\vec y}$
$\newcommand\Vz{\vec z}$
$\newcommand\VA{\vec A}$
$\newcommand\VB{\vec B}$
$\newcommand\VC{\vec C}$
$\newcommand\VD{\vec D}$
$\newcommand\VE{\vec E}$
$\newcommand\VF{\vec F}$
$\newcommand\VG{\vec G}$
$\newcommand\VH{\vec H}$
$\newcommand\VI{\vec I}$
$\newcommand\VJ{\vec J}$
$\newcommand\VK{\vec K}$
$\newcommand\VL{\vec L}$
$\newcommand\VM{\vec M}$
$\newcommand\VN{\vec N}$
$\newcommand\VO{\vec O}$
$\newcommand\VP{\vec P}$
$\newcommand\VQ{\vec Q}$
$\newcommand\VR{\vec R}$
$\newcommand\VS{\vec S}$
$\newcommand\VT{\vec T}$
$\newcommand\VU{\vec U}$
$\newcommand\VV{\vec V}$
$\newcommand\VW{\vec W}$
$\newcommand\VX{\vec X}$
$\newcommand\VY{\vec Y}$
$\newcommand\VZ{\vec Z}$
$\newcommand\Valpha{\vec\alpha}$
$\newcommand\Vbeta{\vec\beta}$
$\newcommand\Vgamma{\vec\gamma}$
$\newcommand\Vdelta{\vec\delta}$
$\newcommand\Vepsilon{\vec\epsilon}$
$\newcommand\Vvarepsilon{\vec\varepsilon}$
$\newcommand\Vzeta{\vec\zeta}$
$\newcommand\Veta{\vec\eta}$
$\newcommand\Vtheta{\vec\theta}$
$\newcommand\Vvartheta{\vec\vartheta}$
$\newcommand\Viota{\vec\iota}$
$\newcommand\Vkappa{\vec\kappa}$
$\newcommand\Vlambda{\vec\lambda}$
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
$\newcommand\VTheta{\vec\Theta}$
$\newcommand\VLambda{\vec\Lambda}$
$\newcommand\VXi{\vec\Xi}$
$\newcommand\VPi{\vec\Pi}$
$\newcommand\VSigma{\vec\Sigma}$
$\newcommand\VUps{\vec\Upsilon}$
$\newcommand\VPhi{\vec\Phi}$
$\newcommand\VPsi{\vec\Psi}$
$\newcommand\VOmega{\vec\Omega}$
$\newcommand\BA{\mib A}$
$\newcommand\BB{\mib B}$
$\newcommand\BC{\mib C}$
$\newcommand\BD{\mib D}$
$\newcommand\BE{\mib E}$
$\newcommand\BF{\mib F}$
$\newcommand\BG{\mib G}$
$\newcommand\BH{\mib H}$
$\newcommand\BI{\mib I}}$
$\newcommand\BJ{\mib J}$
$\newcommand\BK{\mib K}$
$\newcommand\BL{\mib L}$
$\newcommand\BM{\mib M}$
$\newcommand\BN{\mib N}$
$\newcommand\BO{\mib O}$
$\newcommand\BP{\mib P}$
$\newcommand\BQ{\mib Q}$
$\newcommand\BR{\mib R}$
$\newcommand\BS{\mib S}$
$\newcommand\BT{\mib T}$
$\newcommand\BU{\mib U}$
$\newcommand\BV{\mib V}$
$\newcommand\BW{\mib W}$
$\newcommand\BX{\mib X}$
$\newcommand\BY{\mib Y}$
$\newcommand\BZ{\mib Z}$
$\newcommand\Ba{\mib a}$
$\newcommand\Bb{\mib b}$
$\newcommand\Bc{\mib c}$
$\newcommand\Bd{\mib d}$
$\newcommand\Be{\mib e}$
$\newcommand\Bf{\mib f}$
$\newcommand\Bg{\mib g}$
$\newcommand\Bh{\mib h}$
$\newcommand\Bi{\mib i}$
$\newcommand\Bj{\mib j}$
$\newcommand\Bk{\mib k}$
$\newcommand\Bl{\mib l}$
$\newcommand\Bm{\mib m}$
$\newcommand\Bn{\mib n}$
$\newcommand\Bo{\mib o}$
$\newcommand\Bp{\mib p}$
$\newcommand\Bq{\mib q}$
$\newcommand\Br{\mib r}$
$\newcommand\Bs{\mib s}$
$\newcommand\Bt{\mib t}$
$\newcommand\Bu{\mib u}$
$\newcommand\Bv{\mib v}$
$\newcommand\Bw{\mib w}$
$\newcommand\Bx{\mib x}$
$\newcommand\By{\mib y}$
$\newcommand\Bz{\mib z}$\)
$\newcommand\vrh{\varrho}$
$\newcommand\vsig{\varsigma}$
$\newcommand\ups{\upsilon}$
$\newcommand\eps{\epsilon}$
$\newcommand\ve{\varepsilon}$
$\newcommand\vth{\vartheta}$
$\newcommand\vphi{\varphi}$
$\newcommand\xhi{\chi}$
$\newcommand\Ups{\Upsilon}$
$\newcommand\Balpha{\mib\alpha}$
$\newcommand\Bbeta{\mib\beta}$
$\newcommand\Bgamma{\mib\gamma}$
$\newcommand\Bdelta{\mib\delta}$
$\newcommand\Beps{\mib\epsilon}$
$\newcommand\Bve{\mib\varepsilon}$
$\newcommand\Bzeta{\mib\zeta}$
$\newcommand\Beta{\mib\eta}$
$\newcommand\Btheta{\mib\theta}$
$\newcommand\Bvth{\mib\vartheta}$
$\newcommand\Biota{\mib\iota}$
$\newcommand\Bkappa{\mib\kappa}$
$\newcommand\Blambda{\mib\lambda}$
$\newcommand\Bmu{\mib\mu}$
$\newcommand\Bnu{\mib\nu}$
$\newcommand\Bxi{\mib\xi}$
$\newcommand\Bom{\mib\omicron}$
$\newcommand\Bpi{\mib\pi}$
$\newcommand\Bvarpi{\mib\varpi}$
$\newcommand\Brho{\mib\rho}$
$\newcommand\Bvrh{\mib\varrho}$
$\newcommand\Bsigma{\mib\sigma}$
$\newcommand\Bvsig{\mib\varsigma}$
$\newcommand\Btau{\mib\tau}$
$\newcommand\Bups{\mib\upsilon}$
$\newcommand\Bphi{\mib\phi}$
$\newcommand\Bvphi{\mib\vphi}$
$\newcommand\Bchi{\mib\chi}$
$\newcommand\Bpsi{\mib\psi}$
$\newcommand\Bomega{\mib\omega}$
$\newcommand\BGamma{\mib\Gamma}$
$\newcommand\BDelta{\mib\Delta}$
$\newcommand\BTheta{\mib\Theta}$
$\newcommand\BLambda{\mib\Lambda}$
$\newcommand\BXi{\mib\Xi}$
$\newcommand\BPi{\mib\Pi}$
$\newcommand\BSigma{\mib\Sigma}$
$\newcommand\BUps{\mib\Upsilon}$
$\newcommand\BPhi{\mib\Phi}$
$\newcommand\BPsi{\mib\Psi}$
$\newcommand\BOmega{\mib\Omega}$
$\newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}$
$\newcommand\RGamma{ \Gamma}$
$\newcommand\RDelta{ \Delta}$
$\newcommand\RTheta{ \Theta}$
$\newcommand\RLambda{ \Lambda}$
$\newcommand\RXi{ \Xi}$
$\newcommand\RPi{ \Pi}$
$\newcommand\RSigma{ \Sigma}$
$\newcommand\RUps{ \Upsilon}$
$\newcommand\RPhi{ \Phi}$
$\newcommand\RPsi{ \Psi}$
$\newcommand\ROmega{ \Omega}$
$\newcommand\RA{ A}$
$\newcommand\RB{ B}$
$\newcommand\RC{ C}$
$\newcommand\RD{ D}$
$\newcommand\RE{ E}$
$\newcommand\RF{ F}$
$\newcommand\RG{ G}$
$\newcommand\RH{ H}$
$\newcommand\RI{ I}$
$\newcommand\RJ{ J}$
$\newcommand\RK{ K}$
$\newcommand\RL{ L}$
$\newcommand { M}$
$\newcommand\RN{ N}$
$\newcommand\RO{ O}$
$\newcommand\RP{ P}$
$\newcommand\RQ{ Q}$
$\newcommand\RR{ R}$
$\newcommand\RS{ S}$
$\newcommand\RT{ T}$
$\newcommand\RU{ U}$
$\newcommand\RV{ V}$
$\newcommand\RW{ W}$
$\newcommand\RX{ X}$
$\newcommand\RY{ Y}$
$\newcommand\RZ{ Z}$
$\newcommand\Ra{ a}$
$\newcommand\Rb{ b}$
$\newcommand\Rc{ c}$
$\newcommand\Rd{ d}$
$\newcommand\Re{ e}$
$\newcommand\Rf{ f}$
$\newcommand\Rg{ g}$
$\newcommand\Rh{ h}$
$\newcommand\Ri{ i}$
$\newcommand\Rj{ j}$
$\newcommand\Rk{ k}$
$\newcommand\Rl{ l}$
$\newcommand { m}$
$\newcommand\Rn{ n}$
$\newcommand\Ro{ o}$
$\newcommand\Rp{ p}$
$\newcommand\Rq{ q}$
$\newcommand\Rr{ r}$
$\newcommand\Rs{ s}$
$\newcommand\Rt{ t}$
$\newcommand\Ru{ u}$
$\newcommand\Rv{ v}$
$\newcommand\Rw{ w}$
$\newcommand\Rx{ x}$
$\newcommand\Ry{ y}$
$\newcommand\Rz{ z}$
$\newcommand\BBA{\boldsymbol\RA}$
$\newcommand\BBB{\boldsymbol\RB}$
$\newcommand\BBC{\boldsymbol\RC}$
$\newcommand\BBD{\boldsymbol\RD}$
$\newcommand\BBE{\boldsymbol\RE}$
$\newcommand\BBF{\boldsymbol\RF}$
$\newcommand\BBG{\boldsymbol\RG}$
$\newcommand\BBH{\boldsymbol\RH}$
$\newcommand\BBI{\boldsymbol\RI}$
$\newcommand\BBJ{\boldsymbol\RJ}$
$\newcommand\BBK{\boldsymbol\RK}$
$\newcommand\BBL{\boldsymbol\RL}$
$\newcommand\BBM{\boldsymbol }$
$\newcommand\BBN{\boldsymbol\RN}$
$\newcommand\BBO{\boldsymbol\RO}$
$\newcommand\BBP{\boldsymbol\RP}$
$\newcommand\BBQ{\boldsymbol\RQ}$
$\newcommand\BBR{\boldsymbol\RR}$
$\newcommand\BBS{\boldsymbol\RS}$
$\newcommand\BBT{\boldsymbol\RT}$
$\newcommand\BBU{\boldsymbol\RU}$
$\newcommand\BBV{\boldsymbol\RV}$
$\newcommand\BBW{\boldsymbol\RW}$
$\newcommand\BBX{\boldsymbol\RX}$
$\newcommand\BBY{\boldsymbol\RY}$
$\newcommand\BBZ{\boldsymbol\RZ}$
$\newcommand\BBa{\boldsymbol\Ra}$
$\newcommand\BBb{\boldsymbol\Rb}$
$\newcommand\BBc{\boldsymbol\Rc}$
$\newcommand\BBd{\boldsymbol\Rd}$
$\newcommand\BBe{\boldsymbol\Re}$
$\newcommand\BBf{\boldsymbol\Rf}$
$\newcommand\BBg{\boldsymbol\Rg}$
$\newcommand\BBh{\boldsymbol\Rh}\}$
$\newcommand\BBi{\boldsymbol\Ri}$
$\newcommand\BBj{\boldsymbol\Rj}$
$\newcommand\BBk{\boldsymbol\Rk}$
$\newcommand\BBl{boldsymbol\Rl}$
$\newcommand\BBm{\boldsymbol }$
$\newcommand\BBn{\boldsymbol\Rn}$
$\newcommand\BBo{\boldsymbol\Ro}$
$\newcommand\BBp{\boldsymbol\Rp}$
$\newcommand\BBq{\boldsymbol\Rq}$
$\newcommand\BBr{\boldsymbol\Rr}$
$\newcommand\BBs{\boldsymbol\Rs}$
$\newcommand\BBt{\boldsymbol\Rt}$
$\newcommand\BBu{\boldsymbol\Ru}$
$\newcommand\BBv{\boldsymbol\Rv}$
$\newcommand\BBw{\boldsymbol\Rw}$
$\newcommand\BBx{\boldsymbol\Rx}$
$\newcommand\BBy{\boldsymbol\Ry}$
$\newcommand\BBz{\boldsymbol\Rz}$
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
$\newcommand\bnabla{\boldsymbol{\nabla}}$
$\newcommand\Bell{\boldsymbol\ell}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\newcommand\ns{^\vphantom{*}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}$
$\newcommand\izpi{\int\limits_{0}^{\infty}\!\!}$
$\newcommand\etc{\it etc.\/}$
$\newcommand\etal{\it et al.\/}$
$\newcommand\opcit{\it op. cit.\/}$
$\newcommand\ie{\it i.e.\/}$
$\newcommand\Ie{\it I.e.\/}$
$\newcommand\viz{\it viz.\/}$
$\newcommand\eg{\it e.g.\/}$
$\newcommand\Eg{\it E.g.\/}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\def\sss#1{\scriptscriptstyle #1}$
$\def\ss#1{\scriptstyle #1}$
$\def\ssr#1{\scriptstyle #1}$
$\def\ssf#1{\scriptstyle #1}$
$\newcommand\NA{N_{\ssr{\!A}}}$
$\newcommand\lala{\langle\!\langle}$
$\newcommand\rara{\rangle\!\rangle}$
$\newcommand\blan{\big\langle}$
$\newcommand\bran{\big\rangle}$
$\newcommand\Blan{\Big\langle}$
$\newcommand\Bran{\Big\rangle}$
$\newcommand\intl{\int\limits}$
$\newcommand\half{\frac{1}{2}}$
$\newcommand\third{\frac{1}{3}}$
$\newcommand\fourth{\frac{1}{4}}$
$\newcommand\eighth{\frac{1}{8}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\undertext#1{$\underline{\hbox{#1}}$}$
$\newcommand\Tra{\mathop{\textsf{Tr}}\,}$
$\newcommand\det{\mathop{\textsf{det}}\,}$
$\def\tket#1{|  #1 \rangle}$
$\def\tbra#1{\langle #1|}$
$\def\tbraket#1#2{\langle #1  |   #2 \rangle}$
$\def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}$
$\def\sket#1{|  \, #1 \,  \rangle}$
$\def\sbra#1{\langle \,  #1 \, |}$
$\def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}$
$\def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}$
$\def\ket#1{\big| \, #1\, \big\rangle}$
$\def\bra#1{\big\langle \, #1 \, \big|}$
$\def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}$
$\def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}$
$\newcommand\pz{\partial}$
$\newcommand\pzb{\bar{\partial}}$
$\newcommand\svph{\vphantom{\int}}$
$\newcommand\vph{\vphantom{\sum_i}}$
$\newcommand\bvph{\vphantom{\sum_N^N}}$
$\newcommand\nd{^{\vphantom{\dagger}}}$
$\newcommand\ns{^{\vphantom{*}}}$
$\newcommand\yd{^\dagger}$
$\newcommand\zb{\bar z}$
$\newcommand\zdot{\dot z}$
$\newcommand\zbdot{\dot{\bar z}}$
$\newcommand\kB{k_{\sss{B}}}$
$\newcommand\kT{k_{\sss{B}}T}$
$\newcommand\gtau{g_\tau}$
$\newcommand\Htil{\tilde H}$
$\newcommand\pairo{(\phi\nd_0,J\nd_0)}$
$\newcommand\pairm{(\phi\nd_0,J)}$
$\newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}$
$\newcommand\pairmb{(\Bphi\nd_0,\BJ)}$
$\newcommand\pair{(\phi,J)}$
$\newcommand\Hz{H\nd_0}$
$\newcommand\Ho{H\nd_1}$
$\newcommand\Htz{\Htil\nd_0}$
$\newcommand\Hto{\Htil\nd_1}$
$\newcommand\oc{\omega_\Rc}$

$\newcommand \gtwid{\approx}$

$\newcommand\index{\textsf{ind}}$
$\newcommand\csch{\,{ csch\,}}$
$\newcommand\ctnh{\,{ ctnh\,}}$
$\newcommand\ctn{\,{ ctn\,}}$
$\newcommand\sgn{\,{ sgn\,}}$
$\def\tmapright#1{\xrightarrow \limits^{#1}}$
$\def\bmapright#1{\xrightarrow\limits_{#1}}$
$\newcommand\hfb{\hfill\break}$
$\newcommand\Rep{\textsf{Re}\,}$
$\newcommand\Imp{\textsf{Im}\,}$
$\newcommand\ncdot{\!\cdot\!}$
$\def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }$
$\def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }$
$\newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}$

$\def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}$
$\def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}$
$\def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}$
$\def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}$
$\newcommand\subA{\ns_\ssr{A}}$
$\newcommand\subB{\ns_\ssr{B}}$
$\newcommand\subC{\ns_\ssr{C}}$
$\newcommand\subD{\ns_\ssr{D}}$
$\newcommand\subAB{\ns_\ssr{AB}}$
$\newcommand\subBC{\ns_\ssr{BC}}$
$\newcommand\subCD{\ns_\ssr{CD}}$
$\newcommand\subDA{\ns_\ssr{DA}}$
$\def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }$
$\def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}$
$\newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}$
$\newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}$
$\newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}$
$\newcommand\cds{\,\bullet\,}$
$\newcommand\ccs{\,\circ\,}$
$\newcommand\nsub{_{\vphantom{\dagger}}}$
$\newcommand\rhohat{\hat\rho}$
$\newcommand\vrhhat{\hat\vrh}$
$\newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}$
$\newcommand\brangle{\big\rangle}$
$\newcommand\blangle{\big\langle}$
$\newcommand\vet{\tilde\ve}$
$\newcommand\zbar{\bar z}$
$\newcommand\ftil{\tilde f}$
$\newcommand\XBE{\RXi\ns_\ssr{BE}}$
$\newcommand\XFD{\RXi\ns_\ssr{FD}}$
$\newcommand\OBE{\Omega\ns_\ssr{BE}}$
$\newcommand\OFD{\Omega\ns_\ssr{FD}}$
$\newcommand\veF{\ve\ns_\RF}$
$\newcommand\kF{k\ns_\RF}$
$\newcommand\kFu{k\ns_{\RF\uar}}$
$\newcommand\SZ{\textsf Z}}$ \( \newcommand\kFd{k\ns_{\RF\dar}\)
$\newcommand\muB{\mu\ns_\ssr{B}}$
$\newcommand\mutB{\tilde\mu}\ns_\ssr{B}$
$\newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}$
$\newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}$
$\newcommand\xhiOZ{\xhi^\ssr{OZ}}$
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
$\newcommand\jhz{\HJ(0)}$
$\newcommand\nda{\nd_\alpha}$
$\newcommand\ndap{\nd_{\alpha'}}$
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.02:_Phase_Flows_in_Classical_Mechanics), /content/body/p/span, line 1, column 23

\)
$\newcommand\msa{m\ns_\ssr{A}}$
$\newcommand\msb{m\ns_\ssr{B}}$
$\newcommand\mss{m\ns_\Rs}$
$\newcommand\HBx{\hat\Bx}$
$\newcommand\HBy{\hat\By}$
$\newcommand\HBz{\hat\Bz}$
$\newcommand\thm{\theta\ns_m}$
$\newcommand\thp{\theta\ns_\phi}$
$\newcommand\mtil{\widetilde m}$
$\newcommand\phitil{\widetilde\phi}$
$\newcommand\delf{\delta\! f}$
$\newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}$
$\newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}$
$\newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}$
$\newcommand\vbar{\bar v}$
$\newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}$
$\newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}$
$\newcommand\gla{g\nd_{\RLambda\nd}}$
$\newcommand\TA{T\ns_\ssr{A}}$
$\newcommand\TB{T\ns_\ssr{B}}$
$\newcommand\ncdot{\!\cdot\!}$
$\newcommand\NS{N\ns_{\textsf S}}$

Hamiltonian evolution

The master equation provides us with a semi-phenomenological description of a dynamical system’s relaxation to equilibrium. It explicitly breaks time reversal symmetry. Yet the microscopic laws of Nature are (approximately) time-reversal symmetric. How can a system which obeys Hamilton’s equations of motion come to equilibrium?

Let’s start our investigation by reviewing the basics of Hamiltonian dynamics. Recall the Lagrangian $L=L(q,\Dq,t)=T-V$. The Euler-Lagrange equations of motion for the action $S\big[q(t)\big]=\int\!dt\,L$ are

$$\Dp\ns_\sigma={d\over dt}\bigg({\pz L\over\pz \Dq\ns_\sigma}\bigg)={\pz L\over\pz q\ns_\sigma}\ ,$$

where $p\ns_\sigma$ is the canonical momentum conjugate to the generalized coordinate $q\ns_\sigma$:

$$p\nd_\sigma={\pz L\over\pz\Dq_\sigma}\ .$$

The Hamiltonian, $H(q,p)$ is obtained by a Legendre transformation,

$$H(q,p)=\sum_{\sigma=1}^r p\nd_\sigma\,\Dq\nd_\sigma - L\ .$$

Note that

$$\begin{split} dH&=\sum_{\sigma=1}^r\bigg(p\nd_\sigma\,d\Dq\nd_\sigma + \Dq\nd_\sigma\,dp\nd_\sigma -{\pz L\over \pz q_\sigma}\,dq\nd_\sigma -{\pz L\over\pz \Dq_\sigma}\,d\Dq\nd_\sigma\bigg)-{\pz L\over\pz t}\,dt\\\ &=\sum_{\sigma=1}^r\bigg(\Dq\nd_\sigma\,dp\nd_\sigma - {\pz L\over \pz q_\sigma}\,dq\nd_\sigma \bigg)-{\pz L\over \pz t}\,dt\ . \end{split}$$

Thus, we obtain Hamilton’s equations of motion,

$${\pz H\over\pz p_\sigma} = \Dq\nd_\sigma \quad ,\quad {\pz H\over\pz q_\sigma}= -{\pz L\over\pz q_\sigma}=-\Dp\nd_\sigma$$

and

$${dH\over dt} = {\pz H\over\pz t} = -{\pz L\over\pz t}\ .$$

Define the rank $2r$ vector $\Bvphi$ by its components,

$$\varphi\nd_i=\begin{cases} q\nd_i & \hbox{if\ } 1\le i\le r\\ &\\ p\nd_{i-r} & \hbox{if\ } r\le i \le 2r\ . \end{cases}$$

Then we may write Hamilton’s equations compactly as

$${\dot\varphi}_i=J_{ij}\,{\pz H\over\pz\varphi_j}\ ,$$

where

$$J=\begin{pmatrix} 0\nd_{r\times r} & 1\nd_{r\times r} \\ -1\nd_{r\times r} & 0\nd_{r\times r} \end{pmatrix}$$

is a rank $2r$ matrix. Note that $J^\Rt=-J$, $J$ is antisymmetric, and that $J^2=-1\nd_{2r\times 2r}$.

Dynamical systems and the evolution of phase space volumes

Consider a general dynamical system,

$${d\Bvphi\over dt}=\BV(\Bvphi)\ ,$$

where $\Bvphi(t)$ is a point in an $n$-dimensional phase space. Consider now a compact² region $\CR\ns_0$ in phase space, and consider its evolution under the dynamics. That is, $\CR\ns_0$ consists of a set of points $\big\{\Bvphi\,|\,\Bvphi\in\CR\ns_0\big\}$, and if we regard each $\Bvphi\in\CR\ns_0$ as an initial condition, we can define the time-dependent set $\CR(t)$ as the set of points $\Bvphi(t)$ that were in $\CR\ns_0$ at time $t=0$:

$$\CR(t)=\big\{\Bvphi(t) \, \big| \, \Bvphi(0)\in\CR\ns_0\big\}\ .$$

Now consider the volume $\ROmega(t)$ of the set $\CR(t)$. We have

$$\ROmega(t)=\int\limits_{\CR(t)}\!\!\!d\mu$$

where

$$d\mu=d\varphi\ns_1\,d\varphi\ns_2\,\cdots\, d\varphi\ns_n\ ,$$

for an $n$-dimensional phase space. We then have

$$\ROmega(t+dt)=\!\!\!\!\int\limits_{\CR(t+dt)}\!\!\!\!\!\!\!d\mu' = \!\int\limits_{\CR(t)}\!\!\!d\mu\,\bigg|{\pz\varphi\ns_i(t+dt)\over\pz\varphi\ns_j(t)} \bigg|\ ,$$

where

$$\bigg|{\pz\varphi\ns_i(t+dt)\over\pz\varphi\ns_j(t)}\bigg|\equiv{\pz(\varphi'_1,\ldots,\varphi'_n)\over\pz(\varphi\ns_1,\ldots,\varphi\ns_n)}$$

is a determinant, which is the Jacobean of the transformation from the set of coordinates $\big\{\varphi\ns_i=\varphi\ns_i(t)\big\}$ to the coordinates $\big\{\varphi'_i=\varphi\ns_i(t+dt)\big\}$. But according to the dynamics, we have

$$\varphi\ns_i(t+dt)=\varphi\ns_i(t)+V\ns_i\big(\Bvphi(t)\big)\,dt + \CO(dt^2)$$

and therefore

$${\pz\varphi\ns_i(t+dt)\over\pz\varphi\ns_j(t)}=\delta\ns_{ij} + {\pz V\ns_i\over\pz \varphi\ns_j}\,dt + \CO(dt^2)\ .$$

We now make use of the equality

$$\ln{det}\,M = \Tra \ln M\ ,$$

for any matrix $M$, which gives us³, for small $\ve$,

$${det}\,\big(1+\ve A\big)=\exp\Tra \ln\big(1+\ve A\big) = 1+\ve\,\Tra \!A + \half\,\ve^2\Big(\big(\Tra \!A\big)^2 - \Tra (A^2)\Big) + \ldots$$

Thus,

$$\ROmega(t+dt)=\ROmega(t)+\int\limits_{\CR(t)}\!\!\!d\mu\>\bnabla\!\cdot\!\BV\>dt + \CO(dt^2)\ ,$$

which says

$${d\ROmega\over dt}=\!\!\int\limits_{\CR(t)}\!\!\!\!d\mu\>\bnabla\!\cdot\!\BV=\!\!\!\!\!\int\limits_{\pz\CR(t)}\!\!\!\!\!dS\>\nhat\cdot\BV$$

Here, the divergence is the phase space divergence,

$$\bnabla\!\cdot\!\BV=\sum_{i=1}^n{\pz V\ns_i\over\pz \varphi\ns_i}\ ,$$

and we have used the divergence theorem to convert the volume integral of the divergence to a surface integral of $\nhat\cdot\BV$, where $\nhat$ is the surface normal and $dS$ is the differential element of surface area, and $\pz\CR$ denotes the boundary of the region $\CR$. We see that if $\bnabla\!\cdot\!\BV=0$ everywhere in phase space, then $\ROmega(t)$ is a constant, and phase space volumes are preserved by the evolution of the system.

For an alternative derivation, consider a function $\vrh(\Bvphi,t)$ which is defined to be the density of some collection of points in phase space at phase space position $\Bvphi$ and time $t$. This must satisfy the continuity equation,

$${\pz\vrh\over\pz t} + \bnabla\!\cdot\!(\vrh\BV)=0\ .$$

This is called the continuity equation. It says that ‘nobody gets lost’. If we integrate it over a region of phase space $\CR$, we have

$${d\over dt}\int\limits_\CR\!\!d\mu\,\vrh = -\int\limits_\CR\!\!d\mu\,\bnabla\!\cdot\!(\vrh\BV) = -\!\int\limits_{\pz\CR}\!\!dS\> \nhat\cdot(\vrh\BV)\ .$$

It is perhaps helpful to think of $\vrh$ as a charge density, in which case $\BJ=\vrh\BV$ is the current density. The above equation then says

$${dQ\ns_\CR\over dt}=-\!\int\limits_{\pz\CR}\!\!dS\>\nhat\cdot\BJ\ ,$$

where $Q\ns_\CR$ is the total charge contained inside the region $\CR$. In other words, the rate of increase or decrease of the charge within the region $\CR$ is equal to the total integrated current flowing in or out of $\CR$ at its boundary.

Figure $\PageIndex{1}$: Time evolution of two immiscible fluids. The local density remains constant.

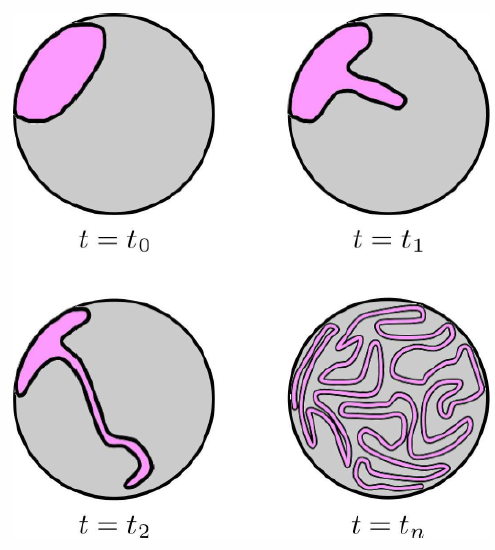
The Leibniz rule lets us write the continuity equation as

$${\pz\vrh\over\pz t} + \BV\ncdot\bnabla\!\vrh + \vrh\,\bnabla\!\cdot\!\BV=0\ .$$

But now suppose that the phase flow is divergenceless, $\bnabla\!\cdot\!\BV=0$. Then we have

$${D\vrh\over Dt}\equiv \bigg({\pz\over\pz t} + \BV\ncdot\bnabla\bigg)\vrh=0\ .$$

The combination inside the brackets above is known as the convective derivative. It tells us the total rate of change of $\vrh$ for an observer moving with the phase flow. That is

$$\begin{split} {d\over dt}\>\vrh\big(\Bvphi(t),t\big)&={\pz\vrh\over\pz\varphi\ns_i}\,{d\varphi\ns_i\over dt} + {\pz\vrh\over\pz t}\\ &=\sum_{i=1}^n V\ns_i\,{\pz\rho\over\pz \varphi\ns_i} +{\pz\vrh\over\pz t}= {D\vrh\over Dt}\ . \end{split}$$

If $D\vrh/Dt=0$, the local density remains the same during the evolution of the system. If we consider the ‘characteristic function’

$$\vrh(\Bvphi,t=0)=\begin{cases} 1 & {if}\ \Bvphi\in \CR\ns_0\\ 0 & {otherwise}\end{cases}$$

then the vanishing of the convective derivative means that the image of the set $\CR\ns_0$ under time evolution will always have the same volume.

Hamiltonian evolution in classical mechanics is volume preserving. The equations of motion are

$${\dot q}_i=+\,{\pz H\over\pz p_i}\qquad , \qquad {\dot p}_i=-\,{\pz H\over\pz q_i}$$

A point in phase space is specified by $r$ positions $q\ns_i$ and $r$ momenta $p\ns_i$, hence the dimension of phase space is $n=2r$:

$$\Bvphi=\begin{pmatrix} \Bq\\ \Bp \end{pmatrix} \qquad,\qquad \BV=\begin{pmatrix} {\dot\Bq} \\ {\dot\Bp} \end{pmatrix}=\begin{pmatrix} \ \pz H/\pz\Bp \\ - \pz H / \pz\Bq \end{pmatrix}\ .$$

Hamilton’s equations of motion guarantee that the phase space flow is divergenceless:

$$\begin{split} \nabla\!\cdot\!\BV&=\sum_{i=1}^r \bigg\{{\pz {\dot q}_i\over\pz q_i} + {\pz {\dot p}_i\over\pz p_i}\bigg\}\\ &=\sum_{i=1}^r \Bigg\{{\pz\over\pz q_i} \bigg({\pz H\over \pz p_i}\bigg) + {\pz\over\pz p_i} \bigg(-{\pz H\over \pz q_i}\bigg)\Bigg\}=0\ . \end{split}$$

Thus, we have that the convective derivative vanishes, viz.

$${D\vrh\over Dt}\equiv {\pz\vrh\over\pz t} + \BV\!\cdot\!\nabla\!\vrh=0\ ,$$

for any distribution $\vrh(\Bvphi,t)$ on phase space. Thus, the value of the density $\vrh(\Bvphi(t),t)$ is constant, which tells us that the phase flow is incompressible. In particular, phase space volumes are preserved.

Liouville’s equation and the microcanonical distribution

Let $\vrh(\Bvphi)=\vrh(\Bq,\Bp)$ be a distribution on phase space. Assuming the evolution is Hamiltonian, we can write

$${\pz\vrh\over\pz t}=-{\dot\Bvphi}\cdot\bnabla\!\vrh = - \sum_{k=1}^r\bigg({\dot q}\ns_k\,{\pz\over\pz q\ns_k} + {\dot p}\ns_k\,{\pz\over\pz p\ns_k}\bigg)\,\vrh=-i\HL\vrh\ ,\label{liouville}$$

where ${\hat L}$ is a differential operator known as the Liouvillian:

$$\HL=-i\sum_{k=1}^r\Bigg\{{\pz H\over\pz p\ns_k}\,{\pz\over\pz q\ns_k}- {\pz H\over\pz q\ns_k}\,{\pz\over\pz p\ns_k}\Bigg\}\ .$$

Equation $\ref{liouville}$, known as Liouville’s equation, bears an obvious resemblance to the Schrödinger equation from quantum mechanics.

Suppose that $\Lambda\ns_a(\Bvphi)$ is conserved by the dynamics of the system. Typical conserved quantities include the components of the total linear momentum (if there is translational invariance), the components of the total angular momentum (if there is rotational invariance), and the Hamiltonian itself (if the Lagrangian is not explicitly time-dependent). Now consider a distribution $\vrh(\Bvphi,t)=\vrh(\Lambda\ns_1,\Lambda\ns_2,\ldots,\Lambda\ns_k)$ which is a function only of these various conserved quantities. Then from the chain rule, we have

$${\dot\Bvphi}\cdot\bnabla\!\vrh=\sum_a\,{\pz\vrh\over\pz\Lambda\ns_a}\>{\dot\Bvphi}\cdot\bnabla\!\Lambda\ns_a =0\ ,$$

since for each $a$ we have

$${d\Lambda\ns_a\over dt}=\sum_{\sigma=1}^r\bigg({\pz \Lambda\ns_a\over\pz q\ns_\sigma} \>\Dq\ns_\sigma + {\pz \Lambda\ns_a\over\pz p\ns_\sigma} \> \Dp\ns_\sigma \bigg) ={\dot\Bvphi}\cdot\bnabla\!\Lambda\ns_a=0\ .$$

We conclude that any distribution $\vrh(\Bvphi,t)=\vrh(\Lambda\ns_1,\Lambda\ns_2,\ldots,\Lambda\ns_k)$ which is a function solely of conserved dynamical quantities is a stationary solution to Liouville’s equation.

Clearly the microcanonical distribution,

$$\vrh\ns_E(\Bvphi)={\delta\big(E-H(\Bvphi)\big) \over D(E)}={\delta\big(E-H(\Bvphi)\big) \over \int\!\!d\mu\, \delta\big(E-H(\Bvphi)\big) }\ ,$$

is a fixed point solution of Liouville’s equation.