2.3b Forces and Types of Energy
- Page ID
- 2851
Some Useful Forces and Energies to Know About
Force of Gravity
An object near the surface of the Earth is attracted to the Earth with a force commonly referred to as the force of gravity. This force is proportional to the object’s mass and fairly constant everywhere on the surface of the Earth. The constant of proportionality is often referred to as “g,” but properly it should have a subscript “E” to indicate that it is the earth that is interacting with the object, and not, e.g., the moon. If the downward force of gravity is balanced by an upward force acting on the object, then the object’s velocity remains constant (balanced forces). If the object exerting the upward force on the object is a scale or balance, then it reads the “weight” of the object, which is equal in this case of balanced forces, to the gravitational force acting down on the object.
The term weight is often taken to mean the gravitational force. This is OK when forces are balanced and the object’s motion does not change. If the object’s velocity is changing, the weight (what a scale reads) can be very different from the gravitational force. (The force of gravity acting on the astronauts in the space shuttle is only slightly less than the force of gravity acting on them when they are standing on Earth, yet they are “weightless” in the orbiting shuttle! We study the interesting state of weightlessness in Part 2 of this course.)
Keeping in mind the reservation mentioned above, we can write:
\[ F_{gravity} = \text{weight} = mg \]
where m is the mass of the object and g = 9.8 N/kg near the surface of the Earth. With mass expressed in kilograms and g in units of N/kg, the weight will be in newtons, N, the SI unit of force. Note that “g” with the value 9.8 N/kg refers only to the value of g near the surface of the Earth. The value of g on the moon or on Mars will have a different value.
Note: This gravity equation is an extremely accurate approximation when near the surface of the Earth, but it will not hold if the object changes elevation by a sizeable fraction of the Earth's radius. You will learn the full story later, with Newton's theory of gravity.
Example: A Stone and a Freight Train
The acceleration of an object can be computed by adding up all the forces on an object, and dividing by its mass.
\[ a = \frac{F}{m} \]
A stone and a freight train cart are dropped at the same time from the top of the empire state building. Which hits the ground first?
The stone has a mass of 4 kg, while the freight train cart has a mass of 4500 kg.
Solution
The object with larger acceleration will hit the ground first. Ignoring air resistance, the only force acting on the rock and the train cart is gravity.
\( F_{rock} = m_{rock}g \) and \( F_{train} = m_{train}g \)
To compute the acceleration, divide the force by the mass.
\( a_{rock} = \frac{ F_{rock}}{ m_{rock} } \) and \( a_{train} = \frac{ F_{train}}{ m_{train} } \)
But the force is mg to begin with! So dividing by m leaves only g, so
\[ a_{rock} = a_{train} = g = 9.8 m/s^{2} \]
So the two hit the ground at the same time!
If this is true, the units N/kg should be equivalent to m/s2. 1 N = 1 kg-m/s2, so indeed the units work out correctly.
Gravitational Potential Energy
A gravitational potential energy-system exists for each pair of objects interacting by the gravitational force. If we are talking about an object and the Earth, the energy of this system changes as some other object (perhaps you) does work on the object by raising it to a higher elevation. We call this a change in the gravitational potential energy, ∆PEgravity, of the Earth-object system. This change is simply equal to the work done by the other object and is
\[ \Delta GPE = mg\Delta y \]
where ∆y is the change in elevation of the object. Notice that ∆GPE does not depend on distance moved parallel to the surface of the Earth, but only on the change in vertical distance (gravitational force points toward the center of the Earth). The work done on the Earth-object system by something else moving the object further from the center of the Earth, is positive, because the force and change in distance are in the same direction.
Also note that we are imagining that the object is lifted up at a constant speed, so that there is no change in its motion. Thus, all of the work goes into changing the gravitational potential energy of the system. We call this a “potential” energy, because the energy depends only on the relative positions of the object and Earth. It does not depend on the route taken to get to these positions or on the speeds the object and Earth might have.
Note that our expression for the gravitational potential energy gives only changes. Where we put our origin of the coordinate system used to measure “y” does not matter, since we are always subtracting two elevations. If we get sloppy and say an object has a gravitational potential energy of so many joules, we mean it has this amount relative to where we picked the origin of our coordinate system, which is completely arbitrary.We will come back to this later, but it is worth noting here that there is a connection between the force and the change in the potential energy.
A Note on the "Zero Point" for Potential Energies
Energy of Motion–Kinetic Energy
Now suppose we do work on an object and move it in a horizontal direction, increasing its speed. Because we have not changed its elevation, we have not changed its gravitational potential energy. But certainly it now has more energy. We know this both from experience and from our definition of work. So where did the energy go? It is in the object’s motion. We call this kinetic energy, or KE and sometimes K in equations.
The KE of an object in motion at speed \(v\) with mass \(m\) is given by:
\[KE = \dfrac{1}{2}mv^{2}\]
In addition, if we do work on an object of mass \(m\) and change its velocity from \(v_{i}\) to \(v_{f}\), then the change in KE is
\[ W = \Delta KE = KE_{f} - KE{i} = \dfrac{1}{2}mv_{f}^{2} - \dfrac{1}{2}mv_{i}^{2} \]
Note: it is the difference of the squares of the speeds that is important in changes in KE.
Prototypical Example of Mechanical Energy Conservation
A roller coaster with mass of 8,000 kg on a frictionless track reaches an initial height of 100 m, before plummeting to just 10 m above the ground. How much potential energy was lost by the coaster? Where did this energy go?
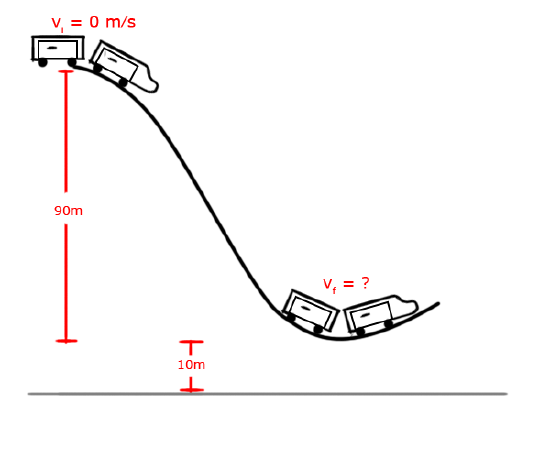Solution
To discuss potential energy, let's use the ground as a reference, so that an object at ground level has zero potential energy (we're allowed to do this because only changes in energy are relevant; the zero point can be shifted arbitrarily).
Then the roller coaster starts off with \( GPE_{i} = mgy_{i} = (8,000kg)(9.8m/s)(100m) = 7,840,000 J = 7.84 MJ \)
And at the bottom has a final potential \( GPE_{f} = mgy_{f} = (8,000kg)(9.8m/s)(10m) = 784,000 J = .784 MJ \)
(1 MJ is a mega joule, which is one million joules.)
This leaves a change of \( \Delta GPE = .784 MJ - 7.84MJ = -7.056 MJ \)
Making Sense of This Answer (Negative Energy?)
This number does not indicate direction in the way that vectors do, since energy is a scalar. Rather, it simply indicates that the amount of energy in the roller-coaster system has decreased by 7.056 MJ. When working with energy, the question always then becomes "where did the energy go?".
In this case, the answer is that the energy went into the carts kinetic energy only, since the friction was said to be negligible.
Extra: How Fast is the Cart At the Bottom?
It turns out energy conservation can tell us how fast the cart moves at any given altitude. Energy conservation tells us that, for a closed system
\[ \Delta KE + \Delta GPE = 0 \]
which means that the cart gains as much kinetic energy as it lost potential energy. This means
\[ \Delta KE = - \Delta GPE = - (-7.056 MJ) = 7.056 MJ \]
Because we know the cart's mass, the velocity can be computed from the kinetic energy equation:
\[ KE = \dfrac{1}{2}mv^{2} \]
\[ \sqrt{ \dfrac{2 KE}{m} } = v\]
\[ \sqrt{ \dfrac{2(7,056,000 J)}{8,000kg} } = 42 m/s \]
(Checking to see if this makes sense: 42 m/s is about 94 mph. This is a little fast for a roller coaster at that height, but then again we neglected friction!)
The next energy system we take up is so important for future work, that we give it its own model: the Intro Spring-Mass Oscillator Model.