2.3a Work
- Page ID
- 2061
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We are ready to make sense of the idea of work as the transfer of energy from one physical system to another, or from one object to another.
Work Definition
Work, \(W\), is a transfer of energy from one physical system to another via a force acting between the two. The energy transfer is defined by a force that acts through a displacement. Only the part of the force that acts parallel to the displacement contributes to work.
The mathematical expression to calculate work is:
\[ W = \vec{F} \cdot \vec{\Delta x} = \left \| \vec{F} \right \| \left \| \vec{\Delta x} \right \| cos(\theta) \label{eq1}\]
where \( \vec{F} \) is the force as a vector, and \( \vec{\Delta x} \) is the displacement, also as a vector. Click here for more on the vector dot product.
When Does Work Happen?
In order to accomplish work on an object there must be a force exerted on the object and it must move in the direction of the force. If either of those conditions are not met, then there is no work. For example, if an object is traveling freely with no forces acting on it, there is no work being done on the object despite it moving through distance. The reverse is also true: if an object has a force acting on it, but is not moving, there is also no work being done. Imagine a tug-o-war match with equally strong opponents, each exerting a large force on the rope, but where the rope never moves. Both opponents may feel as though they are working hard, but a physicist would say that neither of them does any work! There is one last way for no work to be done. Imagine someone carrying a weight across a room while walking at a constant speed. Your intuition may be tempted to tell you that there is a force being exerted through a distance, and therefore work is being done, but as is often the case in physics, your intuition would be wrong! The force you exert while carrying an object is entirely up, but the displacement while walking is completely horizontal. The best way to improve your intuition about work is to work through examples, apply the definition, and see where it leads you.
Like heat, work is a scalar (i.e., has no direction associated with it) and is measured in the SI unit of energy, joules. A joule is equivalent to a newton·meter, or J = N·m, since a newton is the SI unit of force.
Here are a couple of examples to get you started calculating work on your own.
Example \(\PageIndex{1}\): Work When Force and Displacement Are Parallel
Mario pushes a box through 10m on level ground, applying a force of 20N to the box in the direction of motion. How much work does he do on the box?
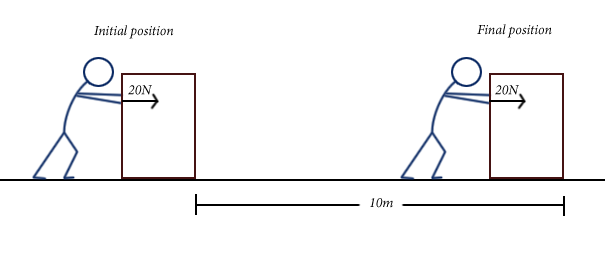
Solution
There is an important distinction between this example where the box is pushed and a situation where the box is carried. As shown in the figure, in this pushing example, the force is to the right, in the same direction as the displacement. This situation satisfies both conditions for work being done, so we should expect to get a positive answer.
Applying the definition of work (Equation \ref{eq1}):
\[ W = \vec{F} \cdot \vec{\Delta x} = \left \| \vec{F} \right \| \left \| \vec{\Delta x} \right \| cos(\theta) \nonumber \]
We are told the magnitudes \( \left \| \vec{F} \right \| \) and \( \left \| \vec{\Delta x} \right \| \), as well as that they both point in the same direction (to the right, as shown in the picture), meaning the angle \(\theta\) between the two is 0. This gives us
\[ \left \| \vec{F} \right \| \left \| \vec{\Delta x} \right \| cos(0) = \left \| \vec{F} \right \| \left \| \vec{\Delta x} \right \| \cdot 1 \]
because \(cos(0) = 1\). Finally, we can substitute in the values for force and displacement given, and arrive at a simple answer
\[W = (10m)(20N) = 200J \]
When the force and displacement are parallel, the work is simply the product of their magnitudes. This is a useful fact to remember to speed up calculations.
This is the amount of energy used by a standard 100 Watt light bulb in two seconds.
Example \(\PageIndex{1}\): Work When Force and Displacement are Not Parallel
A box is pulled by a rope which makes and angle of 60° with the horizontal. The rope pulls with a force of 15N while the box slides a distance of 2m. How much work does the rope do on the box?
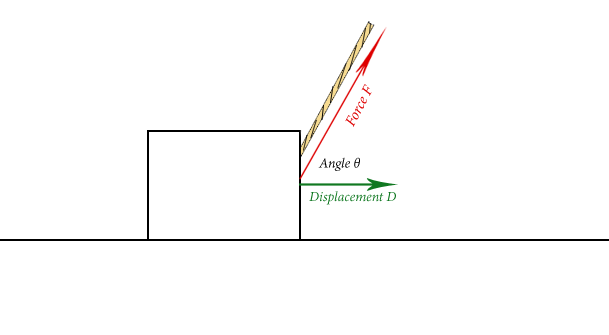
Solution
From looking at the picture it's clear that there is force acting at least partially in the direction of movement, so we should expect to get a positive answer again. However, there is a non-zero angle between the displacement and the force, meaning the dot product will be important now. Using the definition of work again:
\[ W = \vec{F} \cdot \vec{\Delta x} = \left \| \vec{F} \right \| \left \| \vec{\Delta x} \right \| cos(\theta) \]
If we substitute in the given values we get:
\[ W = (15N)(2m)cos(60°) = 15J \]
Do On Your Own
Working out the consequences on your own is an extremely important part of learning.
Thought Exercise: On Force and Energy Conservation
Given that work is a transfer of energy, can you think of an argument as to why forces always come in equal and opposite pairs?
HINT: Think about energy conservation and the definition of work.
Thought Exercise: Work and Speed
A light car and a heavy car have the same engine, causing both to experience the same force when driven. In a race lasting 1000m, the lighter car zips ahead, winning the race easily. The question is, which car had more work done on it during the race?
- The lighter car, as it traveled much faster through the race.
- The heavier car, as it took more force to get it moving.
- Equal work, because they had the same engine and traveled the same distance.


