5.12: Gravitational Potential of any Massive Body
( \newcommand{\kernel}{\mathrm{null}\,}\)
You might just want to look at Chapter 2 of Classical Mechanics (Moments of Inertia) before proceeding further with this chapter.
In figure VIII.26 I draw a massive body whose centre of mass is C, and an external point P at a distance R from C. I draw a set of Cxyz axes, such that P is on the z-axis, the coordinates of P being (0,0,z). I indicate an element δm of mass, distant r from \text{C} and l from \text{P}. I’ll suppose that the density at δm is ρ and the volume of the mass element is δτ, so that δm = ρδτ.
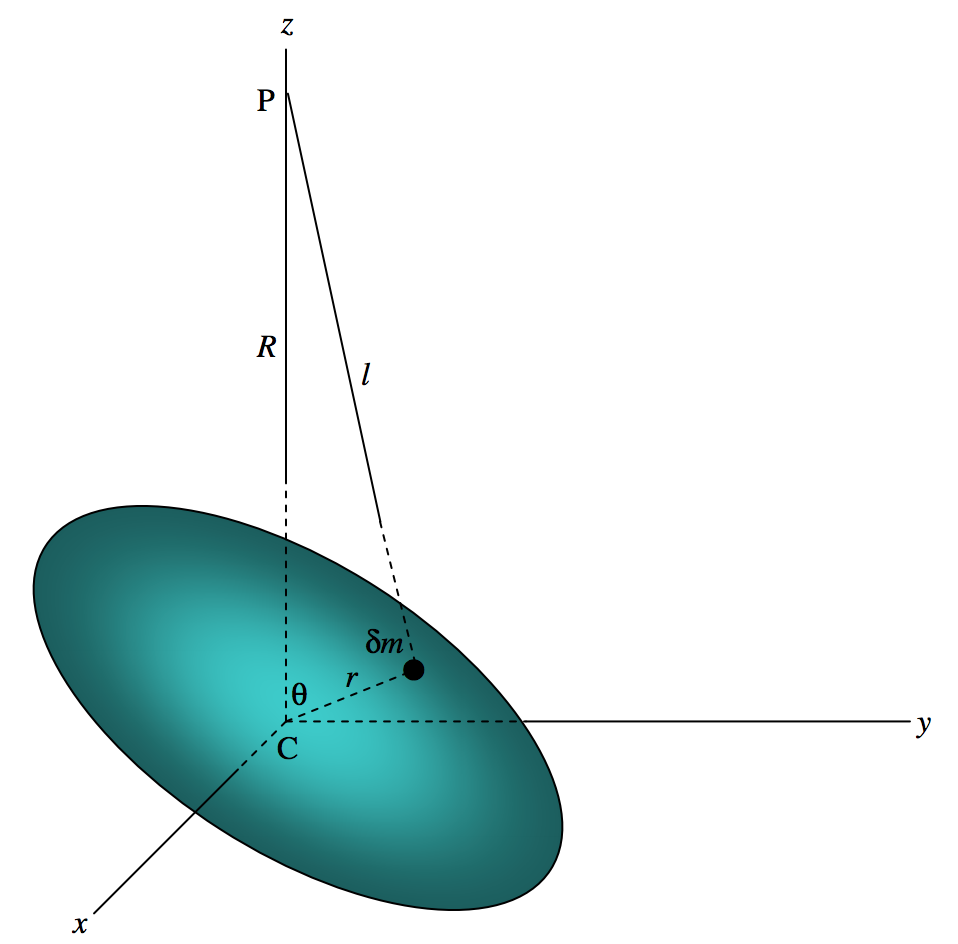
\text{FIGURE V.26}
The potential at \text{P} is
ψ = -G \int \frac{dm}{l} = -G \int \frac{ρdτ}{l}. \label{5.12.1} \tag{5.12.1}
But l^2 = R^2 + r^2 - 2Rr \cos 2 θ,
so ψ = -G \left[ \frac{1}{R} \int ρ dτ + \frac{1}{R^2} \int ρ r \cos θ d τ + \frac{1}{R^3} \int ρ r^2 P_2 (\cos θ) dτ + \frac{1}{R^4} \int ρ r^3 P_3 (\cos θ) d τ ... \right]. \label{5.12.2} \tag{5.12.2}
The integral is to be taken over the entire body, so that ∫ ρdτ = M, where M is the mass of the body. Also ∫ ρr \cos θd τ = \int z dm, which is zero, since \text{C} is the centre of mass. The third term is
\frac{1}{2R^3} \int ρ r^2 (3 \cos^2 θ - 1) dτ = \frac{1}{2R^3} \int ρ r^2 (2-3\sin^2 θ ) dτ . \label{5.12.3} \tag{5.12.3}
Now
\int 2 ρ r^2 d τ = \int 2r^2 d m = \int \left[ (y^2 + z^2) + (z^2 + x^2) + (x^2 + y^2) \right] dm = A + B + C
where A, B and C are the second moments of inertia with respect to the axes \text{C}x, \text{C}y, \text{C}z respectively. But A + B + C is invariant with respect to rotation of axes, so it is also equal to A_0 + B_0 + C_0, where A_0, \ B_0, \ C_0 are the principal moments of inertia.
Lastly, \int ρ r^2 \sin^2 θ dτ is equal to C, the moment of inertia with respect to the axis \text{C}z.
Thus, if R is sufficiently larger than r so that we can neglect terms of order (r/R)^3 and higher, we obtain
ψ = - \frac{GM (2MR^2 + A_0 + B_0 + C_0 -3C)}{2R^3}. \label{5.12.4} \tag{5.12.4}
In the special case of an oblate symmetric top, in which A_0 = B_0 < C_0, and the line \text{CP} makes an angle γ with the principal axis, we have
C = A_0 + (C_0 - A_0) \cos^2 γ = A_0 + (C_0 - A_0) Z^2/R^2, \label{5.12.5} \tag{5.12.5}
so that ψ = -\frac{G}{R} \left[ M + \frac{C_0 - A_0}{2R^2} \left( 1 - \frac{3Z^2}{R^2} \right) \right]. \label{5.12.6} \tag{5.12.6}
Now consider a uniform oblate spheroid of polar and equatorial diameters 2c and 2a respectively. It is easy to show that
C_0 = \frac{2}{5} Ma^2. \label{5.12.7} \tag{5.12.7}
Confirm Equation \ref{5.12.7}.
It is slightly less easy to show (Exercise: Show it.) that
A_0 = \frac{1}{5} M \left( a^2 + c^2 \right) . \label{5.12.8} \tag{5.12.8}
For a symmetric top, the integrals of the odd polynomials of Equation \ref{5.12.2} are zero, and the potential is generally written in the form
ψ = - \frac{GM}{R} \left[ 1 + \left( \frac{a}{R} \right)^2 J_2 P_2 (\cos γ) + \left( \frac{a}{R} \right) J_4 P_4 (\cos γ) ... \right] \label{5.12.9} \tag{5.12.9}
Here γ is the angle between \text{CP} and the principal axis. For a uniform oblate spheroid, J_2 = \frac{C_0 - A_0}{Mc^2}. This result will be useful in a later chapter when we discuss precession.


