21.4: Hooke’s Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
We imagine a particle whirling around on the end of a spring, oscillating in and out as it does so. The force constant of the spring is k, the force on the particle is −kr and the potential (elastic) energy is V=12kr2. This is akin to a non-rigid rotor.

The effective potential energy is therefore
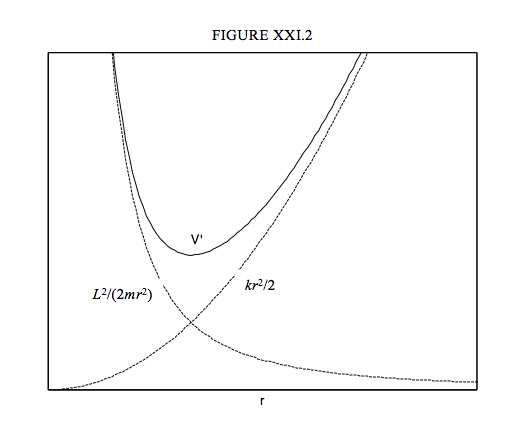
V′=12kr2+L22mr2.
and is sketched in Figure XVI.2. The total energy (potential + kinetic) is constant (independent of r) and is greater than (or equal to) the potential energy. The distance of the particle from the centre of attraction is bounded above and below. The motion is a Lissajous ellipse, with the centre of attraction at the centre (not the focus) of the ellipse. The lower bound is the semi minor axis and the upper bound is the semi major axis.
An inverse square force (e.g. a gravitational force, or a Coulomb’s law electrostatic force) and a Hooke’s law force (kx) are obvious examples of real forces in nature. In what follows we shall investigate the behavior of a particle under the influence of other force laws, such as inverse fourth power and inverse cube forces. It is difficult to imagine whether such forces actually exist in nature (the field of an electric dipole falls off as the cube of the distance - but the field is not radial, and the force is not a central force), and to that extent much of what follows is an exercise in mathematics more than in physics. But inverse square and Hooke’s law forces are certainly not the only forces to operate in nature. What is the force law, for example, for the residual strong interactions between nucleons in an atomic nucleus, or the force law between the quarks within a nucleon? It will be worthwhile investigating the simpler hypothetical forces to be discussed here in order to understand the principles and methods that may be applicable to a more difficult problem.


