4.8: Force-free Motion of a Rigid Symmetric Top
( \newcommand{\kernel}{\mathrm{null}\,}\)
Notation:
- I1, I2, I3 are the principal moments of inertia. I3 is the unique moment. If it is the largest of the three, the body is an oblate symmetric top; if it is the smallest, it is a prolate spherical top.
- Ox0, Oy0, Oz0 are the corresponding body-fixed principal axes.
- ω1, ω2, ω3 are the components of the angular velocity vector ω with respect to the principal axes.
In the analysis that follows, we are going to have to think about three vectors. There will be the angular momentum vector L, which, in the absence of external torques, is fixed in magnitude and in the direction in laboratory space. There will be the direction of the axis of symmetry, the Oz0 axis, which is fixed in the body, but not necessarily in space, unless the body happens to be rotating about its axis of symmetry; we’ll denote a unit vector in this direction by ˆz0. And there will be the instantaneous angular velocity vector ω which is neither space- nor body-fixed.
What we are going to find is the following. We shall find that ω precesses in the body about the body-fixed symmetry axis in a cone called the body cone. The angle between ω and ˆz0 is constant (we’ll be calling this angle α), and the magnitude ω of ω of is constant. We shall find that the sense of the precession is the same as the sense of the spin if the body is oblate, but opposite if it is prolate. The direction of the symmetry axis, however, is not fixed in space, but it precesses about the space-fixed angular momentum vector L in another cone. This cone is narrower than the body cone if the body is oblate, but broader than the body cone if the body is prolate. The net result of these two precessional motions is that precesses ω in space about the space-fixed angular momentum vector in a cone called the space cone. For a prolate top, the semi vertical angle of the space cone can be anything from 0° to 90°; for an oblate top, however, the semi vertical angle of the space cone cannot exceed 19° 28' . That’s quite a lot to take in in one breath!
We can start with Euler’s equations of motion for force-free rotation of a symmetric top:
I1˙ω1=−ω2ω3(I3−I1),I1˙ω2=−ω1ω3(I3−I1),I3˙ω3=0.
From the first of these we obtain the result
ω3=constant
For brevity, I am going to let
(I3−I1)I1=Ω,
although in a moment Ω will have a physical meaning.
Equations 4.8.1 and 4.8.2 become:
˙ω1=Ωω2
and
˙ω2=Ωω1
Eliminate ω2 from these to obtain
˙ω1=−Ω2ω1
This is the Equation for simple harmonic motion and its solution is
ω1=ω0cos(Ωt+ϵ)
in which ω0 and ϵ, the two constants of integration, whose values depend on the initial conditions in the usual fashion, are the amplitude and initial phase angle. On combining this with Equation 4.8.6, we obtain
ω2=ω0sin(Ωt+ϵ)
From these we see that (ω21+ω22)1/2, which is the magnitude of the component of ω in the x0y0-plane, is constant, equal to ω0; and since ω3 is also constant, it follows that (ω21+ω22+ω23)1/2, which is the magnitude of ω, is also constant. The cosine of the angle α between ^z0 and ω is ω3/(ω21+ω22+ω23)1/2, and its sine is ω0/(ω21+ω22+ω23)1/2, so that α is constant. Equations 4.8.9 and 4.8.10 tell us, then, that the vector ω is precessing around the symmetry axis at an angular speed Ω. Making use of Equation 4.8.5, we find that
cosα=ω3ω=I1Ω(I3−I1)ω
If we take the direction of the z0 axis to be the direction of the component of ω along the symmetry axis, then Ω is in the same direction as z0 if I3>I1 (that is, if the top is oblate) and it is in the opposite direction if the top is prolate. The situation for oblate and prolate tops is shown in Figure IV.11.
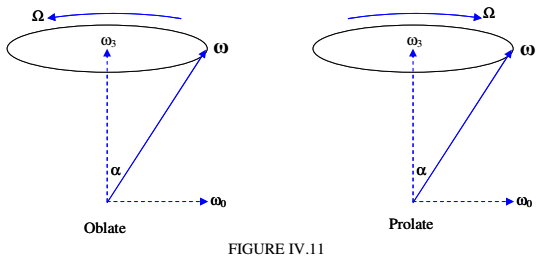
We have just dealt with how the instantaneous axis of rotation precesses about the body-fixed symmetry axis, describing the body cone of semi vertical angle α.
Now we are going to consider the precession of the body-fixed symmetry axis about the space-fixed angular momentum vector L. I am going to make use of the idea of Eulerian angles for expressing the orientation of one three-dimensional set of axes with respect to another. If you are not already familiar with Eulerian angles or would like a refresher, you can go to to Chapter 3 of Celestial Mechanics especially Section 3.7.
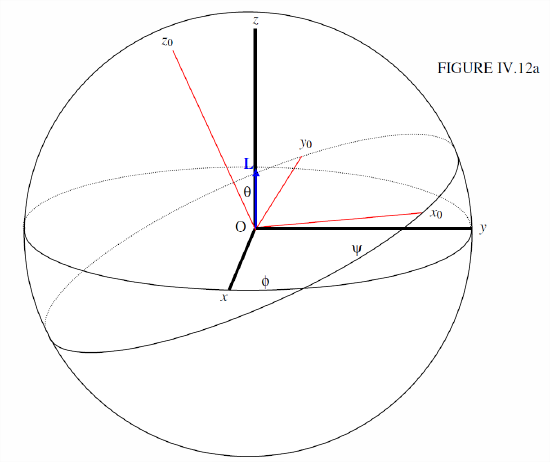
Recall that we are using Ox0y0z0 for body-fixed coordinates, referred to the principal axes. I shall use Oxyz for space-fixed coordinates, and there is no loss of generality if I choose the Oz axis to coincide with the angular momentum vector L. Let me try to draw the situation in Figure IV.12a. The axes Oxyz are the space-fixed axes. The axes Ox0y0z0 are the body-fixed principal axes. The angular momentum vector L is directed along the axis Oz. The symmetry axis of the body is directed along the axis Oz0. The Eulerian angles of the body-fixed axes relative to the space fixed axes are (ϕ, θ, ψ).
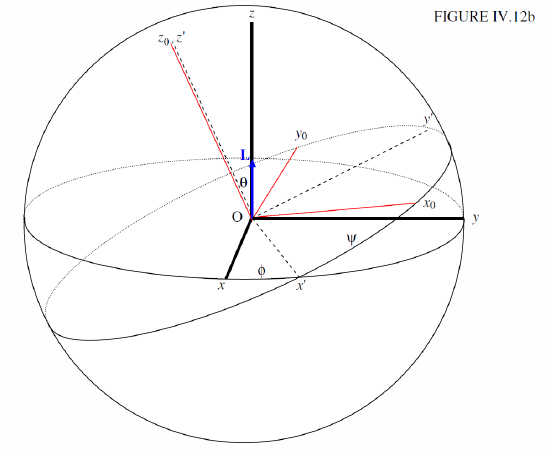
Recall, with the aid of Figure IV.12b, how these Euler angles are formed:
First, a rotation by ϕ about Oz. Second, a rotation by θ about the dashed line Ox′ to form an intermediate set of axes Ox′y′z′ . Third, a rotation by ψ about Oz′ to form the body- fixed principal axes Ox0y0z0.
Spend a little time trying to visualize these three sets of axes. Please also convince yourself, from the way the Euler angles were formed through three rotations, that the vector L is in the y′z′ plane and has no x′ component. It is also in the y0z0 plane and has no x0 component.
You will then agree that
Lx′=0,Ly′=LsinθLz′=Lcosθ.
Now if Lx′=0, then ωx′ is also zero, which means that ω, like L, is in the y′z′ plane.
We have seen that ω makes an angle α with the symmetry axis Oz0, where α is given by Equation 4.8.11.
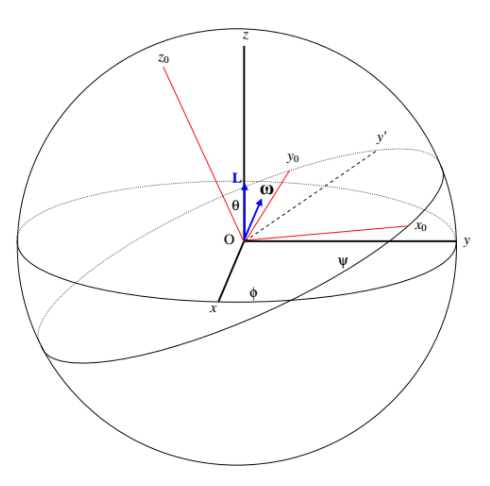
I’ll now add ω to the drawing to make Figure IV.13. Like L, it is in the y'z' plane and has no x' component. I haven’t marked in the angle α. I leave it to your imagination. It is the angle between ω and z0. You should easily agree that
ωx′=0,ωy′+ωsinα,ωz′=ωcosα.
From these, together with Ly′=I1ωy′ and Lz′=I1ωz′ we obtain
I1=tanα=I3tanθ
- For an oblate symmetric top, I3>I1, α>θ.
- For a prolate symmetric top, I3<I1, α<θ.
Now ω can be written as the vector sum of the rates of change of the three Euler angles:
ω=˙θ+˙ϕ+˙ψ
The components of ˙θ and ˙ψ along Oy′ are each zero, and therefore the component of ω along Oy′ is equal to the component of ˙ψ along Oy' .
∴ωsinα=˙ϕsinθ
In summary, then:
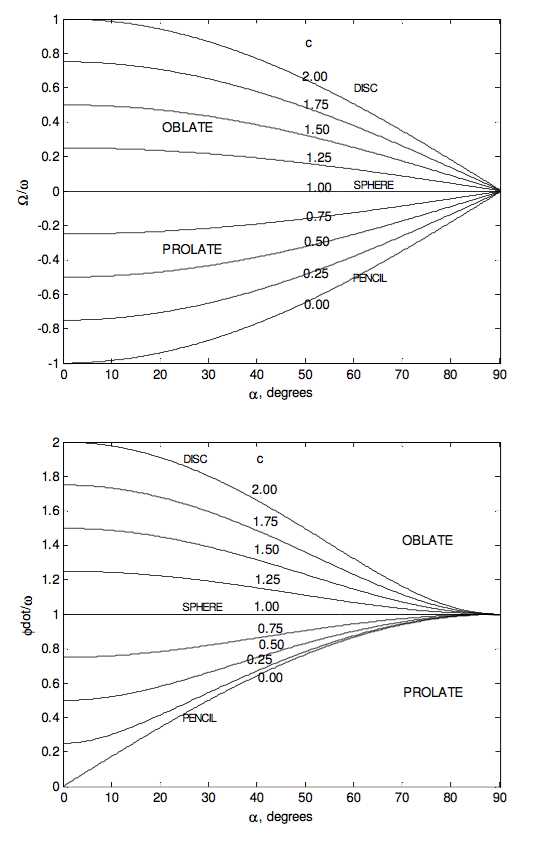
- The instantaneous axis of rotation, which makes an angle α with the symmetry axis, precesses around it at angular speed Ω=I3−I1I1ωcosα which is in the same sense as ω if the top is oblate and opposite if it is prolate.
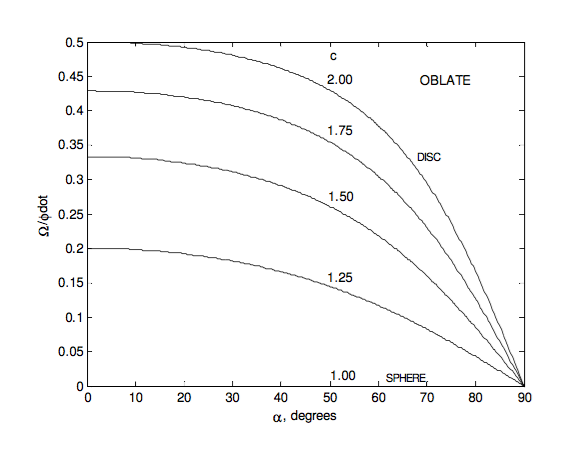
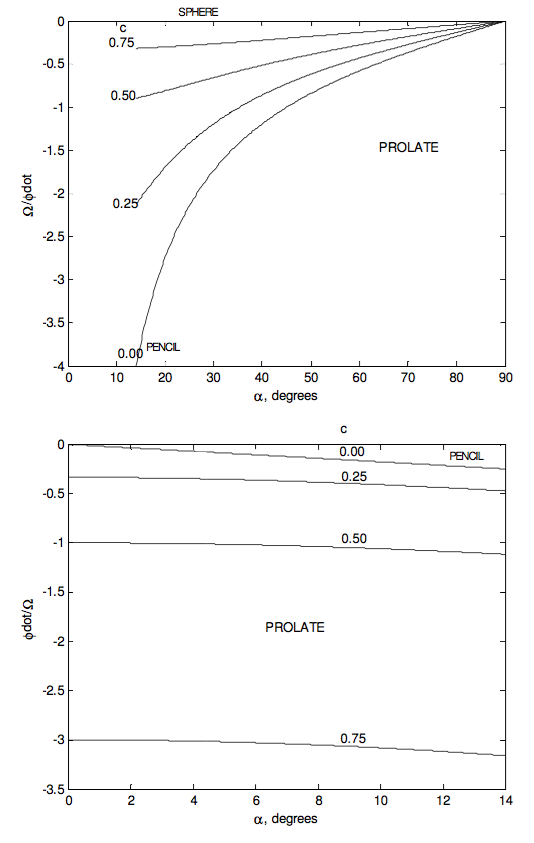
- The symmetry axis makes an angle θ with the space-fixed angular momentum vector L, where tanθ=I1I3tanα. For an oblate top, θ < α. For a prolate top, θ > α.
- The speed of precession of the symmetry axis about L is ˙ϕ=sinαsinθω, or, by elimination of θ between 4.8.18 and 4.8.19, ˙ϕ=[1+I23−I21I13cos2α]1/2ω.
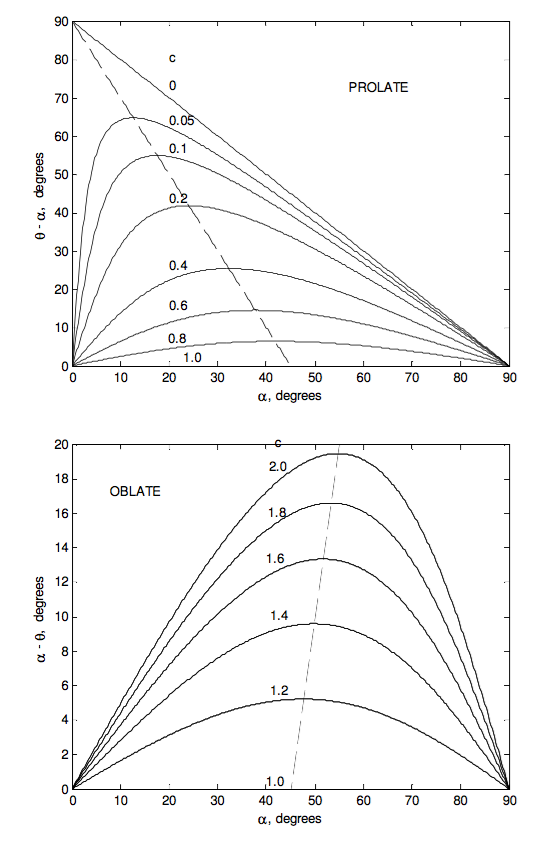
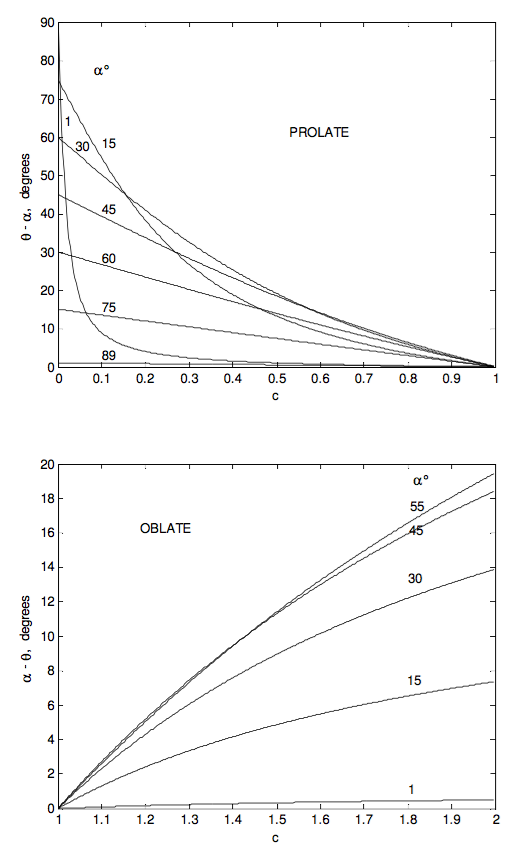
The net result of this is that ω preceses about L at a rate ˙ϕ in the space cone, which has a semi-vertical angle α − θ for an oblate rotator, and θ − α for a prolate rotator. The space cone is fixed in space, while the body cone rolls around it, always in contact, ω being a mutual generator of both cones. If the rotator is oblate, the space cone is smaller than the body cone and is inside it. If the rotator is prolate, the body cone is outside the space cone and can be larger or smaller than it.
Write
c=I3/I1
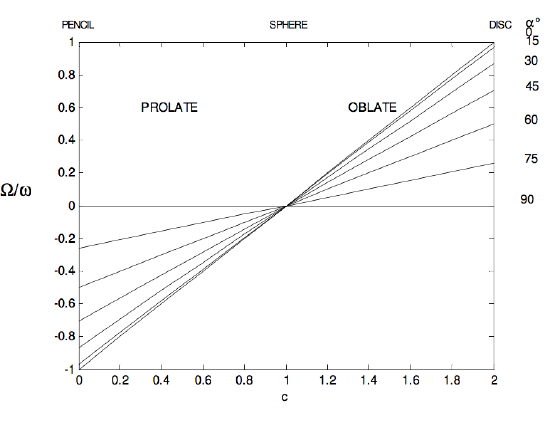
for the ratio of the principal moments of inertia. Note that for a pencil, c=0; for a sphere, c=1; for a plane disc or any regular plane lamina, c=2. (The last of these follows from the perpendicular axes theorem.) The range of c, then, is from 0 to 2, 0 to 1 being prolate, 1 to 2 being oblate.
Equations 4.8.17 and 4.8.20 can be written
Ωω=(c−1)cosα
and
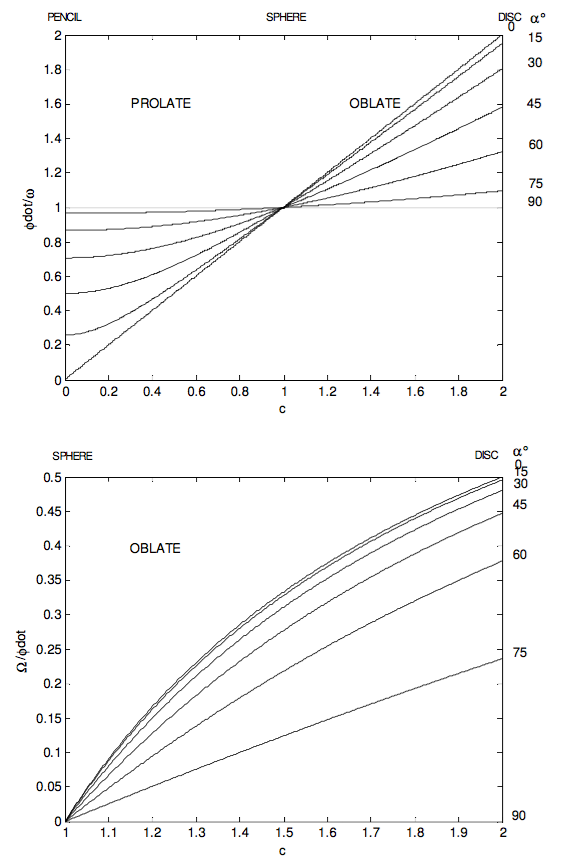
˙ϕω=[1+(c2−1)cos2α]1/2
Figures IV.15 and IV.16 show, for an oblate and a prolate rotator respectively, the instantaneouss rotation vector ω precessing around the body-fixed symmetry axis at a rate Ω in the body cone of semi vertical angle α; the symmetry axis precessing about the space-fixed angular momentum vector L at a rate ˙ϕ in a cone of semi vertical angle θ (which is less than α for an oblate rotator, and greater than α for a prolate rotator; and consequently the instantaneous rotation vector ω precessing around the space-fixed angular momentum vector L at a rate ˙ϕ in the space cone of semi vertical angle α − θ (oblate rotator) or θ − α (prolate rotator).
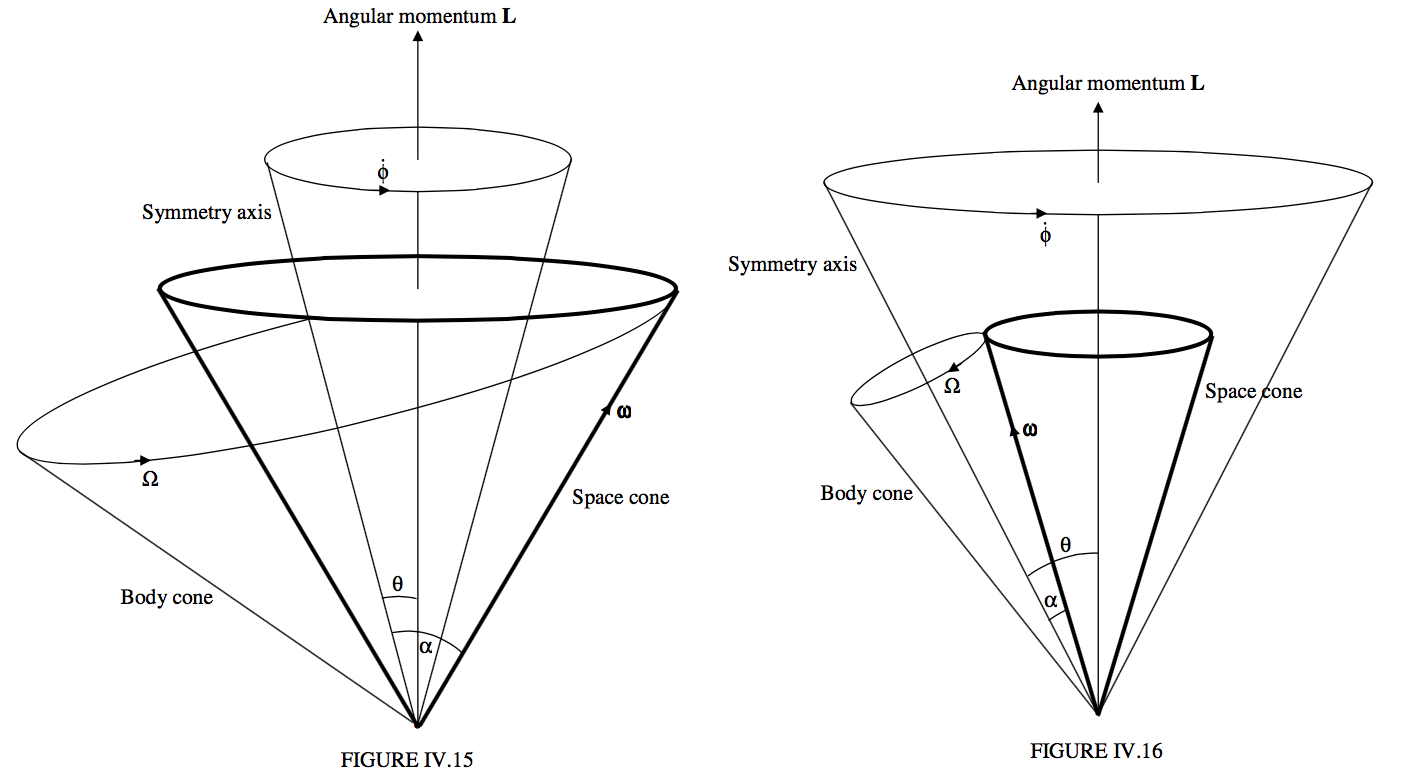
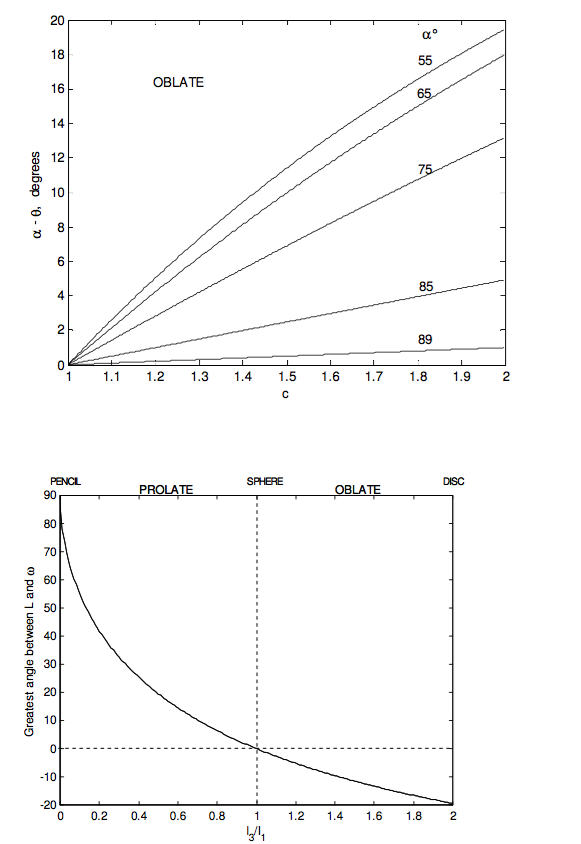
One can see from figures IV.15 and 16 that the angle between L and ω is limited for an oblate rotator, but it can be as large as 90° for a prolate rotator. The angle between L and ω is θ − α (which is negative for an oblate rotator). We have
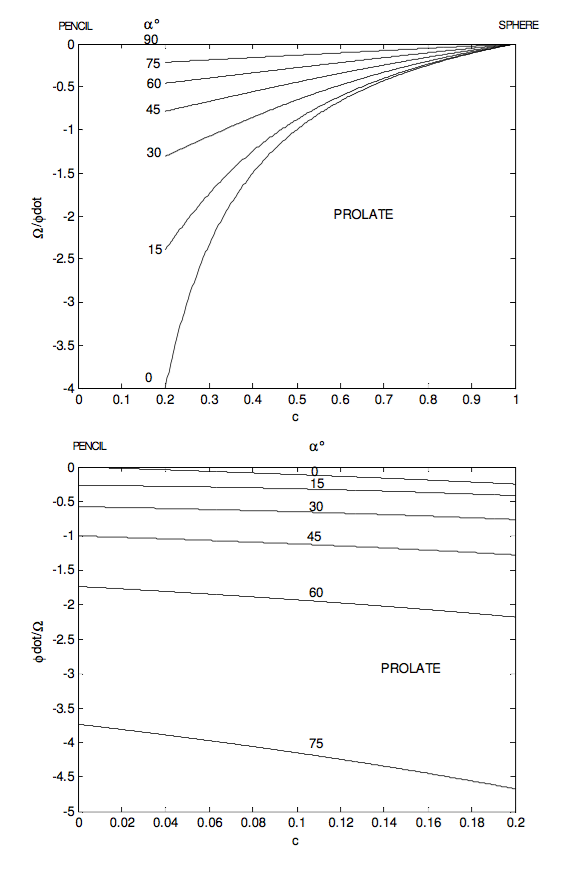
tan(θ−α)=tanθ−tanα1+tanθtanα=(1−c)tanαc+tan2α
By calculus this reaches a maximum value of 1−c2√c for tanα=√c
For a rod or pencil (prolate), in which c=0, the angle between L and ω can be as large as 90°. Recalling exactly what are meant by the vectors L and ω, the reader should try now and imagine in his or her mind’s eye a pencil rotating so that L and ω are at right angles. The spin vector ω is along the length of the pencil and the angular momentum vector L is at right angles to the length of the pencil.
For an oblate rotator, the angle between L and ω is limited. The most oblate rotator is a flat disc or any regular flat lamina. The parallel axis theorem shows that for such a body, c=2. The greatest angle between L and ω for a disc occurs when tanα=√2α = 54° 44'),and then tanα−θ=1√8, α−θ =19° 28'.
In the following figures I illustrate some of these results graphically. The ratio I3I1 goes from 0 for a pencil through 1 for a sphere to 2 for a disc.
Our planet Earth is approximately an oblate spheroid, its dynamical ellipticity (I3−I1)I1 being about 3.285 × 10−3. It is not rotating exactly abut its symmetry axis; the angle α between ω and the symmetry axis being about one fifth of an arcsecond, which is about six metres on the surface. The rotation period is one sidereal day (which is a few minutes shorter than 24 solar hours.) Equation 4.8.17 tells us that the spin axis precesses about the symmetry axis in a period of about 304 days, all within the area of a tennis court. The actual motion is a little more complicated than this. The period is closer to 432 days because of the nonrigidity of Earth, and superimposed on this is an annual component caused by the annual movement of air masses. This precessional motion of a symmetric body spinning freely about an axis inclined to the symmetry axis gives rise to variations of latitude of amplitude about a fifth of an arcsecond. It is not to be confused with the 26,000 year period of the precession of the equinoxes, which is caused by external torques from the Moon and the Sun.


