2.5: Exercise Problems

In each of Problems 2.1-2.11, for the given system:

(i) introduce a set of convenient generalized coordinate(s) $q_{j}$,

(ii) write down the Lagrangian $L$ as a function of $q_{j}, \dot{q}_{j}$, and (if appropriate) time,

(iii) write down the Lagrange equation(s) of motion,

(iv) calculate the Hamiltonian function $H$; find out whether it is conserved,

(v) calculate energy $E$; is $E=H$ ?; is the energy conserved?

(vi) any other evident integrals of motion?

2.1. A double pendulum - see the figure on the right. Consider only the motion in the vertical plane containing the suspension point.

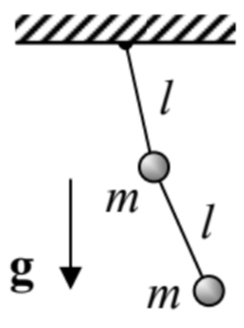
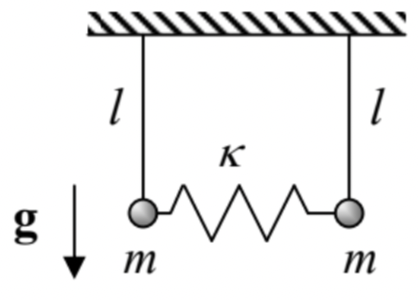
2.2. A stretchable pendulum (i.e. a massive particle hung on an elastic cord that exerts force $F=-\kappa\left(l-l_{0}\right)$, where $\kappa$ and $l_{0}$ are positive constants), also confined to the vertical plane:

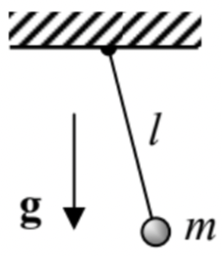
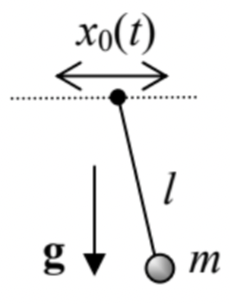
2.3. A fixed-length pendulum hanging from a horizontal support whose motion law $\ x_{0}(t)$ is fixed. (No vertical plane constraint here.)

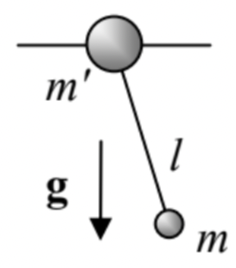
2.4. A pendulum of mass $m$, hung on another point mass $m$ ’, which may slide, without friction, along a straight horizontal rail - see the figure on the right. The motion is confined to the vertical plane that contains the rail.

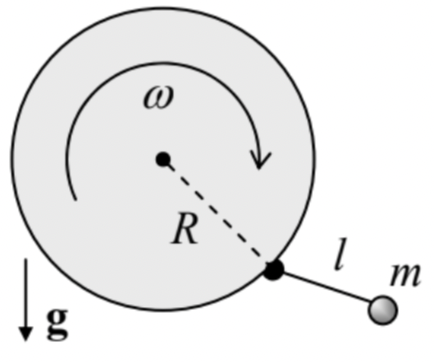
2.5. A point-mass pendulum of length $l$, attached to the rim of a disk of radius $R$, which is rotated in a vertical plane with a constant angular velocity $\omega$ - see the figure on the right. (Consider only the motion within the disk’s plane.)

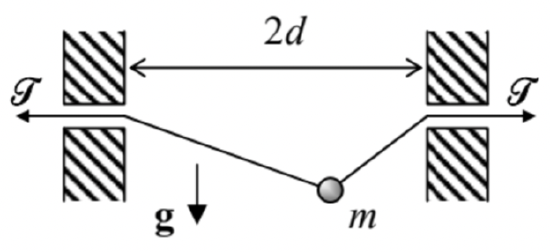
2.6. A bead of mass $m$, sliding without friction along a light string stretched by a fixed force $\mathscr{T}$ between two horizontally displaced points $-$ see the figure on the right. Here, in contrast to the similar Problem 1.10, the string tension $\mathscr{T}$ may be comparable with the bead’s weight $m g$, and the motion is not restricted to the vertical plane.

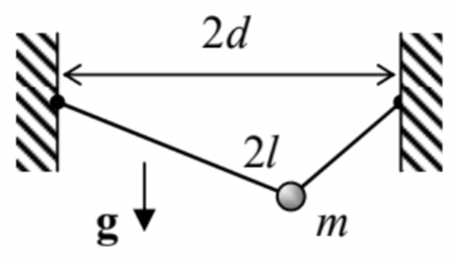
2.7. A bead of mass $m$, sliding without friction along a light string of a fixed length $2 l$, which is hung between two points, horizontally displaced by distance $2 d<2 l-$ see the figure on the right. As in the previous problem, the motion is not restricted to the vertical plane.

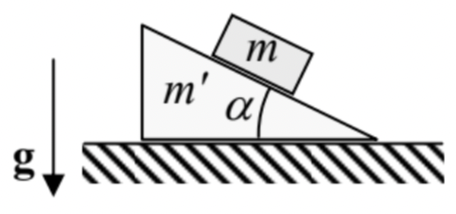
2.8. A block of mass $m$ that can slide, without friction, along the inclined plane surface of a heavy wedge with mass $m$ ’. The wedge is free to move, also without friction, along a horizontal surface - see the figure on the right. (Both motions are within the vertical plane containing the steepest slope line.)

2.9. The two-pendula system that was the subject of Problem 1.8 – see the figure on the right.

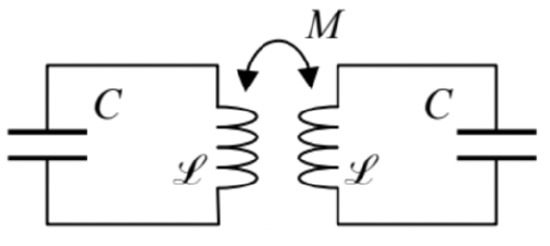
2.10. A system of two similar, inductively-coupled $\ LC$ circuits – see the figure on the right.

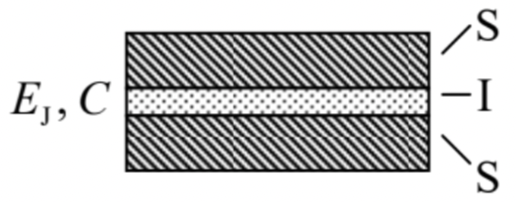
2.11.* A small Josephson junction - the system consisting of two superconductors (S) weakly coupled by Cooper-pair tunneling through a thin insulating layer (I) that separates them - see the figure on the right.

Hints:

(i) At not very high frequencies (whose quantum $\hbar \omega$ is lower than the binding energy $2 \Delta$ of the Cooper pairs), the Josephson effect in a sufficiently small junction may be described by the following coupling energy:

$$U(\varphi)=-E_{\mathrm{J}} \cos \varphi+\text { const }$$ where the constant $E_{J}$ describes the coupling strength, while the variable $\varphi$ (called the Josephson phase difference) is connected to the voltage $V$ across the junction by the famous frequency-to-voltage relation $$\frac{d \varphi}{d t}=\frac{2 e}{\hbar} V,$$ where $e \approx 1.602 \times 10^{-19} \mathrm{C}$ is the fundamental electric charge and $\hbar \approx 1.054 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}$ is the Planck constant. ${ }^{18}$

(ii) The junction (as any system of two close conductors) has a substantial electric capacitance $C$.

---

${ }^{18}$ More discussion of the Josephson effect and the physical sense of the variable $\varphi$ may be found, for example, in EM Sec. $6.5$ and QM Secs. $1.6$ and $2.8$ of this lecture note series, but the given problem may be solved without that additional information.