14.4: The Hyperbola

Cartesian Coordinates

The hyperbola has eccentricity $e>1$. In Cartesian coordinates, it has equation

$$\begin{equation}\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1\end{equation}$$

and has two branches, both going to infinity approaching asymptotes $x=\pm(a / b) y$. The curve intersects the x axis at $x=\pm a, \text { the foci are at } x=\pm a e$ for any point on the curve,

$$\begin{equation}r_{F_{1}}-r_{F_{2}}=\pm 2 a\end{equation}$$

the sign being opposite for the two branches.

Figure $\PageIndex{1}$

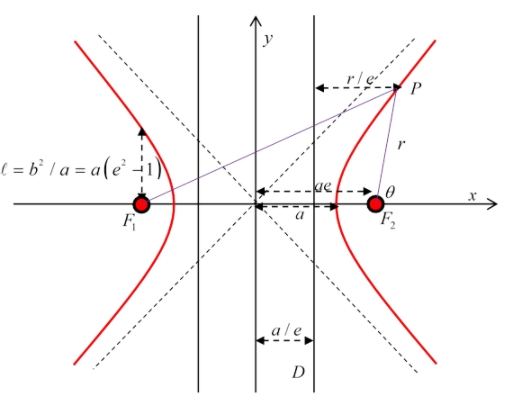
The semi-latus rectum, as for the earlier conics, is the perpendicular distance from a focus to the curve, and is $\ell=b^{2} / a=a\left(e^{2}-1\right)$. Each focus has an associated directrix, the distance of a point on the curve from the directrix multiplied by the eccentricity gives its distance from the focus.

Polar Coordinates

The $(r, \theta)$ equation with respect to a focus can be found by substituting $x=r \cos \theta+a e, y=r \sin \theta$ in the Cartesian equation and solving the quadratic for $u=1 / r$

Notice that $θ$ has a limited range: the equation for the right-hand curve with respect to its own focus $F_{2}$ has

$$\begin{equation}\tan \theta_{\text {asymptote }}=\pm b / a, \text { so } \cos \theta_{\text {asymptote }}=\pm 1 / e\end{equation}$$

The equation for this curve is

$$\begin{equation}\dfrac{\ell}{r}=1-e \cos \theta\end{equation}$$

in the range

$$\begin{equation}\theta_{\text {asymptote }}<\theta<2 \pi-\theta_{\text {asymptote }}\end{equation}$$

This equation comes up with various signs! The left hand curve, with respect to the left hand focus, would have a positive sign $\text { + } e$. With origin at $F_{1}$ (on the left) the equation of the right-hand curve is $\dfrac{\ell}{r}=e \cos \theta-1$ finally with the origin at $F_{2}$ the left-hand curve is $\dfrac{\ell}{r}=-1-e \cos \theta$. These last two describe repulsive inverse square scattering (Rutherford).

Note: A Useful Result for Rutherford Scattering

If we define the hyperbola by

$$\begin{equation}\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1\end{equation}$$

then the perpendicular distance from a focus to an asymptote is just b.

This equation is the same (including scale) as

$$\begin{equation}\ell / r=-1-e \cos \theta, \text { with } \ell=b^{2} / a=a\left(e^{2}-1\right)\end{equation}$$

Figure $\PageIndex{1}$

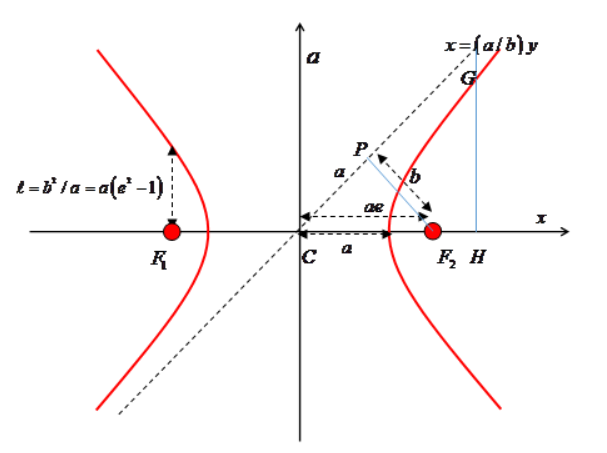
Proof: The triangle $C P F_{2}$ is similar to triangle $C H G, \text { so } P F_{2} / P C=G H / C H=b / a$ and since the square of the hypotenuse $C F_{2} \text { is } a^{2} e^{2}=a^{2}+b^{2}, \text { the distance } F_{2} P=b$

I find this a surprising result because in analyzing Rutherford scattering (and other scattering) the impact parameter, the distance of the ingoing particle path from a parallel line through the scattering center, is denoted by $b$. Surely this can’t be a coincidence? But I can’t find anywhere that this was the original motivation for the notation.