16.3: The Differential Cross Section

In a real scattering experiment, information about the scatterer can be figured out from the different rates of scattering to different angles. Detectors are placed at various angles \((\theta, \phi)\). Of course, a physical detector collects scattered particles over some nonzero solid angle. The usual notation for infinitesimal solid angle is \(d \Omega=\sin \theta d \theta d \phi\). The full solid angle (all possible scatterings) is \(\int d \Omega=4 \pi\) the area of a sphere of unit radius. (Note: Landau uses dο for solid angle increment, but \(d \Omega\) has become standard.)

The differential cross section, written \(d \sigma / d \Omega\) is the fraction of the total number of scattered particles that come out in the solid angle \(d \Omega\), so the rate of particle scattering to this detector is \(n d \sigma / d \Omega, \text { with } n\) the beam intensity as defined above.

Now, we’ll assume the potential is spherically symmetric. Imagine a line parallel to the incoming particles going through the center of the atom. For a given ingoing particle, its impact parameter is defined as the distance its ingoing line of flight is from this central line. Landau calls this \(\rho\), we’ll follow modern usage and call it \(b\).

A particle coming in with impact parameter between \(b\) and \(b+db\) will be scattered through an angle between \(\chi\) and \(\chi+d \chi\) where we’re going to calculate, \(\chi(b)\) by solving the equation of motion of a single particle in a repulsive inverse-square force.

Note: we’ve switched for this occasion from \(\theta \text { to } \chi\) for the angle scattered through because we want to save \(\theta\) for the \((r, \theta)\) coordinates describing the complete trajectory, or orbit, of the scattered particle.

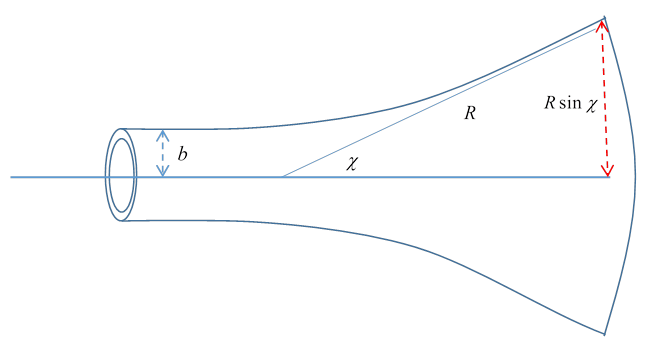
So, an ingoing cross section \(d \sigma=2 \pi b d b\) scatters particles into an outgoing spherical area (centered on the scatterer) \(2 \pi R \sin \chi R d \chi\), that is, a solid angle \(d \Omega=2 \pi \sin \chi d \chi\)

Therefore the scattering differential cross section

\begin{equation}\frac{d \sigma}{d \Omega}=\frac{b(\chi)}{\sin \chi}\left|\frac{d b}{d \chi}\right|\end{equation}

(Note that \(d \chi / d b\) is clearly negative—increasing b means increasing distance from the scatterer, so a smaller \(\chi\))