22.4: Damped Driven Nonlinear Oscillator- Qualitative Discussion

Last updated
Save as PDF

Page ID: 30504

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

We now add to the damped driven linear oscillator a positive quartic potential term, giving equation of motion

\[\ddot{x}+2 \lambda \dot{x}+\omega_{0}^{2} x=(f / m) \cos \gamma t-\beta x^{3}\]

As mentioned above, for a particle oscillating in this potential \(\frac{1}{2} \omega_{0}^{2} x^{2}+\frac{1}{4} \beta x^{4}\) the frequency increases with amplitude: the bigger swings encounter a potential becoming stronger and stronger than the simple harmonic oscillator.

So if we drive the oscillator from rest at the frequency that resonates with its small amplitude oscillations (where the \(\frac{1}{4} \beta x^{4}\) potential term has negligible effect), as the amplitude builds up, the oscillator frequency increases, and the driving force falls out of sync.

The way to keep the amplitude increasing is evidently to gradually increase the frequency of the driving force to match the natural frequency at the increased amplitude. (Side note: this is the principle of the synchrocyclotron except, in that case the frequency is lowered as the energy increases, because the particles go to bigger and bigger orbits as their mases increase relativistically.) This way a small external driving force (enough to overcome frictional damping) can maintain a large amplitude oscillation at a frequency well above the frequency \(\omega_{0}\) of small oscillations.

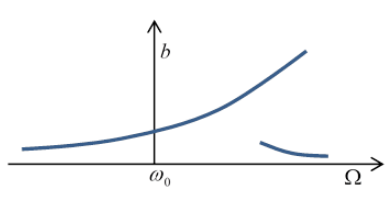
But what if we apply this high frequency to a system initially at rest, rather than gradually ramping up in sync with the oscillations? Then for a small driving force, we can treat the system as a damped simple harmonic oscillator, and this off-resonance force will drive relatively small amplitude oscillations.

The bottom line is that for the same external driving force, with frequency in some range above \(\omega_{0}\), there can be two possible steady state oscillation amplitudes, depending on the history of the system.