4.2: Unit Vectors and Vector Resolution
( \newcommand{\kernel}{\mathrm{null}\,}\)
Recall that the parallelogram law of vector addition is a = \sqrt{b^2 + c^2 +2bc\cos \theta}. This law tells us that if two vectors are mutually perpendicular, we can obtain their magnitude by the Pythagoras theorem. This also means that two mutually perpendicular vectors have a unique contribution to the direction of the resultant. This system is one of the most widely used as it is easy to work with. It is based on the concept of the unit vector.
Unit Vector & Scalar Multiplication of a Vector
A system of unit vectors consists of multiple vectors mutually perpendicular to each other. Further, each unit vector has the magnitude of 1. The magnitude means that we can simply multiply the vector by a scalar quantity to "scale" it. This will be easier to visualize with an example.
Assume a unit vector pointing forward. If you want to move forward 5 units, you would follow the unit vector 5 times. In other words, you repeatedly add the unit vector 5 times. And we know that repeated addition is simply multiplication. Therefore, to move forward 5 units, you follow the vector 5x(Unit Vector). When this concept is applied to the Cartesian plane, we obtain our required tool.
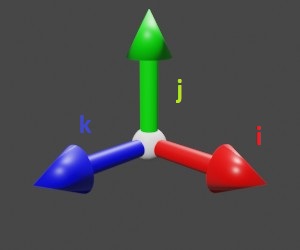
Some points about this system:
- The unit vectors are centered at the origin
- They are ALWAYS mutually perpendicular
- For 3D space, unit vectors corresponding to positive x, y and z are \hat{i}, \hat{j} and \hat{k}
Some examples are given below to help understand the concept.
- Jack moves up 10 meters in an elevator in 3D space. His displacement is 10 \hat{j}
- A cat run diagonally from one corner of a 10 ft x 10 ft room to the opposite corner. Its displacement is 10 \hat{i} + 10 \hat{k}
- Timmy jumps up and down on his bed. When he finally sits down on the bed, his displacement is 0 \times (\hat{i} + \hat{j} + \hat{k})
Vector Resolution
As shown above, a vector can be represented as the sum of scaled unit vectors. The process of obtaining the scaled unit vectors from a vector of a given length is called "resolving" the vector. We use trigonometry and the given angles to obtain the lengths of the side of the various triangles constituting this vector. Here, we shall stick to 2D resolution for the sake of simplicity. However, the concepts are quite easy to carry over into higher dimensions.
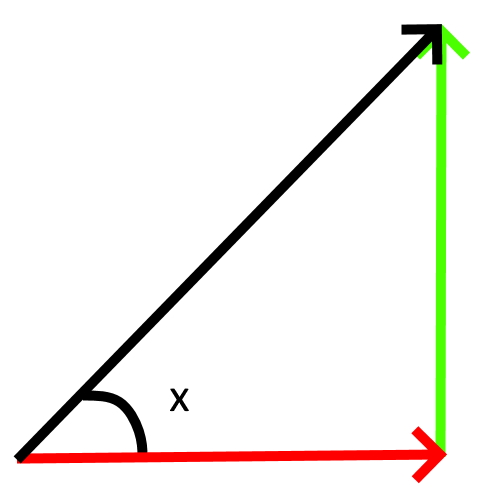
In this example, we can obtain the lengths of the green vector by multiplying the black vector by sin(x). Similarly, the length of the red vector can be obtained by multiplying the black vector with \(\cos (x)\(. The directions of the constituent vectors are positive because the resultant vector lies in the first quadrant of the Cartesian plane, where the x-axis and y-axis are positive. This same concept is used to resolve every vector. The angle is usually measured against the x-axis, with an anti-clockwise angle (above the x-axis) being positive.

