5.5: Tipping Point
( \newcommand{\kernel}{\mathrm{null}\,}\)
Torque
When you hold an object in your hand, the weight of the object tends to cause a rotation of the forearm with the elbow joint acting as the pivot. The tension force applied by your biceps tries to counteract this rotation.
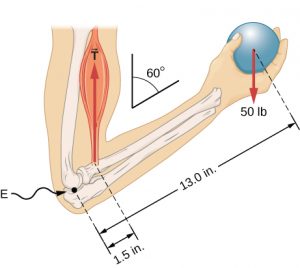
The elbow joint flexed to form a 60° angle between the upper arm and forearm while the hand holds a 50 lb ball. The weight of the ball exerts a torque on the forearm about the elbow joint. Image Credit: Openstax University Physics
When forces applied to an object tend to cause rotation of the object, we say the force is causing a torque. The size of a torque depends on the size of the force, the direction of the force, and the distance from the pivot point to where the force acts.
Reinforcement Activity
The torque caused by a force depends on the distance that force acts from the pivot point. To feel this effect for yourself, try this:
Open a door by pushing perpendicular to the door near the handle, which is far from the pivot point at the hinges.
Now apply the same force perpendicular to the door, but right next to the hinges.
Does the door rotate open just as it did before, or did you have to push with greater force to make the door rotate?
Rotational Equilibrium
The only time a torque wont cause an object to start or stop rotating is when its cancelled out (balanced) by other torques, as we saw for the torque due to biceps tension and torque due to ball weight in the forearm example. When the torques all cancel out the net torque is zero and the object must be in rotational equilibrium. An object in rotational equilibrium might be rotating, but it won’t change it’s rotation speed or direction. If an object in rotational equilibrium is not rotating then it will not start rotating as long as it remains in rotational equilibrium.
Tipping Point
When a body’s center of gravity is above the area formed by the support base the normal force can provide the torque necessary to remain in rotational equilibrium.
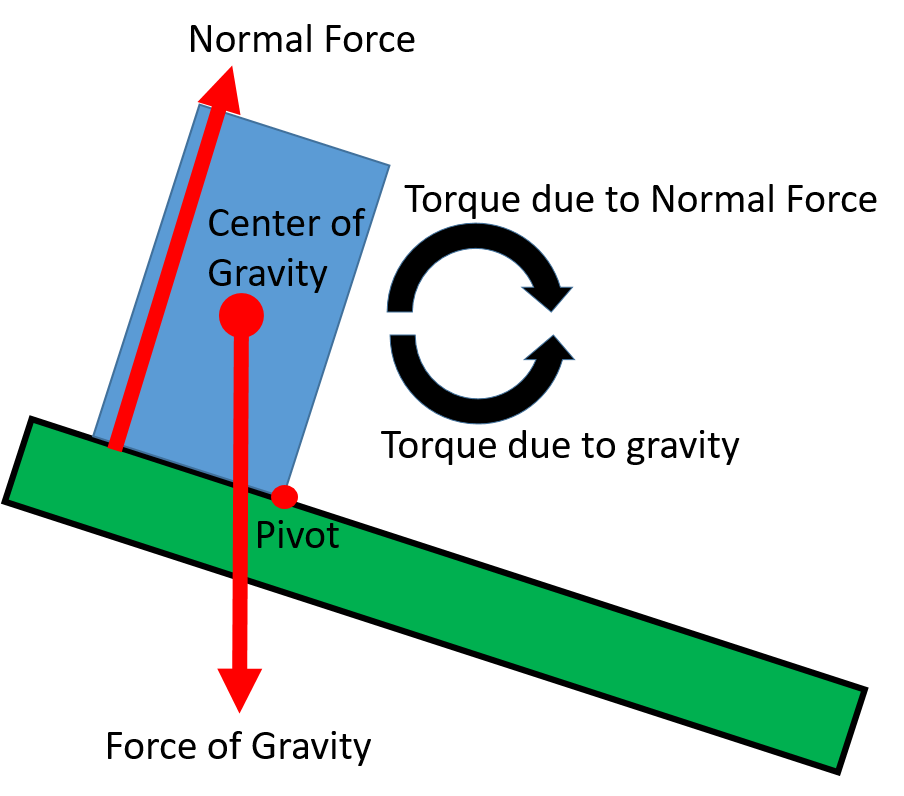
An object in rotational equilibrium. The torque from normal force cancels the torque from gravity.
The critical tipping point is reached when the center of gravity passes outside of the support base. Beyond the tipping point, gravity causes rotation away from the support base, so there is no normal force available to cause the torque needed to cancel out the torque caused by gravity. The normal force acting on the pivot point can help support the object’s weight, but it can’t create a torque because it’s not applied at any distance away from the pivot.
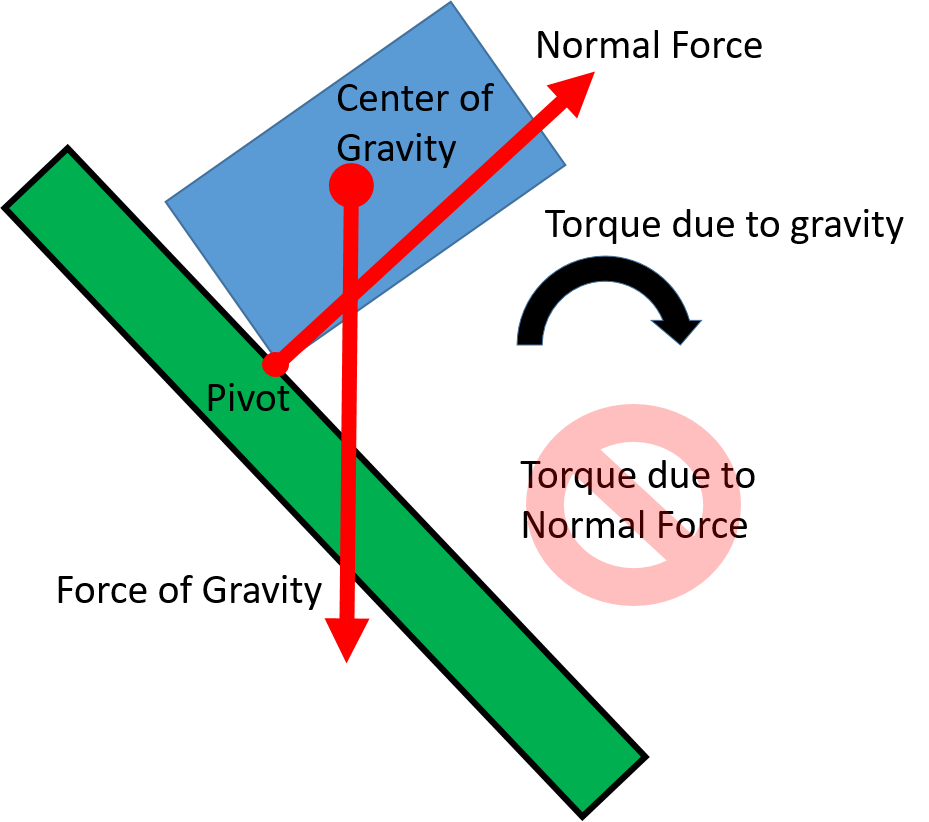
An object out of rotational equilibrium. The normal force acting at the pivot cannot produce a torque to cancel the torque caused by gravity.
Now with a net torque the object can not be in rotational equilibrium. The object will rotate around the edge of the support base and tip over. We often refer to structures (and bodies) that are resistant to tipping over as having greater stability.
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Jul 11, 2018 [1]http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.18. ↵


