6.4: Friction in Joints
( \newcommand{\kernel}{\mathrm{null}\,}\)
Normal Force and Friction in the Elbow
In the previous chapter we found that the upper arm bone (humerus) exerts 480 lbs of force on the pinkie-side forearm bone (ulna) for the scenario shown below:

The elbow joint flexed to form a 60° angle between the upper arm and forearm while the hand holds a 50 lb ball . Image Credit: Openstax University Physics
There are two types of forces that could be acting between the upper and lower arm bones to add up to this total 480 lbs of vertical force. The first is normal force, which we have already learned is the push-back provided by any object in response to being deformed.
Along with normal force, the other force that could occur between two bones is friction ( ). Friction is the force that resists objects sliding against one another. Rub your palms together, the resistance you feel is friction. Complimentary to normal force, which only points perpendicular to surfaces, friction only points parallel to surfaces. Friction can only exist when two objects are attempting to slide past one another, so it is also reactive like normal force. If you don’t try to rub your palms, you don’t feel any resistance. Of course two surfaces have to touch to have friction, so you can’t get friction without normal force. In fact, frictional force is proportional to normal force.
). Friction is the force that resists objects sliding against one another. Rub your palms together, the resistance you feel is friction. Complimentary to normal force, which only points perpendicular to surfaces, friction only points parallel to surfaces. Friction can only exist when two objects are attempting to slide past one another, so it is also reactive like normal force. If you don’t try to rub your palms, you don’t feel any resistance. Of course two surfaces have to touch to have friction, so you can’t get friction without normal force. In fact, frictional force is proportional to normal force.

Frictional forces always oppose motion or attempted motion between objects in contact. Friction arises in part because of the roughness of the surfaces in contact, as seen in the expanded view. In order for the object to move, it must rise to where the peaks can skip along the bottom surface. Thus a force is required just to set the object in motion. Some of the peaks will be broken off, also requiring a force to maintain motion. Much of the friction is actually due to attractive forces between molecules making up the two objects, so that even perfectly smooth surfaces are not friction-free. Such adhesive forces also depend on the substances the surfaces are made of, explaining, for example, why rubber-soled shoes slip less than those with leather soles.
Reinforcement Activity
Rub your palms together. Now push your palms together hard and try to slide them at the same time.
Now the normal force is larger causing the frictional force to grow in proportion.
There are two categories of friction. Static friction( ) acts between two surfaces when they are attempting to slide past one another, but have not yet started sliding. Static friction is a reactionary force because it only exists when some other force is pushing an object to attempt to cause it to slide across a surface. Static friction adjusts to maintain equilibrium with whatever other force is doing the pushing or pulling, but static friction has a maximum value. If the applied force gets larger than the maximum static frictional value, then static friction can’t maintain equilibrium and the object will slide. Kinetic friction (
) acts between two surfaces when they are attempting to slide past one another, but have not yet started sliding. Static friction is a reactionary force because it only exists when some other force is pushing an object to attempt to cause it to slide across a surface. Static friction adjusts to maintain equilibrium with whatever other force is doing the pushing or pulling, but static friction has a maximum value. If the applied force gets larger than the maximum static frictional value, then static friction can’t maintain equilibrium and the object will slide. Kinetic friction ( ) acts whenever two surfaces are sliding past one another, whether or not some other force is pushing the object to keep it sliding. If there is not another force pushing the object to keep is sliding, then kinetic friction will eventually stop the sliding object, but we will learn more about that later. Static friction is larger than kinetic friction. Choose the friction simulation from the simulation set to see how static and kinetic friction behave.
) acts whenever two surfaces are sliding past one another, whether or not some other force is pushing the object to keep it sliding. If there is not another force pushing the object to keep is sliding, then kinetic friction will eventually stop the sliding object, but we will learn more about that later. Static friction is larger than kinetic friction. Choose the friction simulation from the simulation set to see how static and kinetic friction behave.
https://openoregon.pressbooks.pub/bodyphysics/?p=473
Reinforcement Activity
Place a heavy box or book or other object on a desk, table, or the floor. Push the object with your hand, but not hard enough to make it slide. At this point static friction is reacting to your push and exerting a force to perfectly balance your push. The balance between static friction and your push keeps the object in static equilibrium and it doesn’t move.
Now push the object hard enough that it starts to slide. Notice that starts with a jerk. The jerky motion occurs because static friction is larger than kinetic friction. After you “break” static friction and the object starts to move and kinetic friction kicks. Kinetic friction is smaller than static friction so the object jerks forward before you have time to react and decrease your push force to match up with the smaller kinetic friction.
We now know that friction force is proportional to normal force and that there are two types of friction, static and kinetic. The final concept that affects friction is the roughness, or alternatively the smoothness, of the two surfaces. The coefficient of friction ( ) is a unitless number that rates the roughness and is typically determined experimentally. The static frictional force is larger than the kinetic frictional forces because
) is a unitless number that rates the roughness and is typically determined experimentally. The static frictional force is larger than the kinetic frictional forces because  is larger than
is larger than  . Take a look at the table of static and kinetic friction coefficients found below. You can find more values in this massive table of static friction coefficients.
. Take a look at the table of static and kinetic friction coefficients found below. You can find more values in this massive table of static friction coefficients.
 |  | 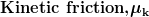 |
|---|---|---|
| Rubber on dry concrete | 1.0 | 0.7 |
| Rubber on wet concrete | 0.7 | 0.5 |
| Wood on wood | 0.5 | 0.3 |
| Waxed wood on wet snow | 0.14 | 0.1 |
| Metal on wood | 0.5 | 0.3 |
| Steel on steel (dry) | 0.6 | 0.3 |
| Steel on steel (oiled) | 0.05 | 0.03 |
| Teflon on steel | 0.04 | 0.04 |
| Bone lubricated by synovial fluid | 0.016 | 0.015 |
| Shoes on wood | 0.9 | 0.7 |
| Shoes on ice | 0.1 | 0.05 |
| Ice on ice | 0.1 | 0.03 |
| Steel on ice | 0.4 | 0.02 |
 . When someone asks a question like, “what is the
. When someone asks a question like, “what is the  of ice?” they usually mean between ice and ice, but its best to avoid asking such questions and just always reference two surfaces.
of ice?” they usually mean between ice and ice, but its best to avoid asking such questions and just always reference two surfaces.Max static friction before release:
(1)

Kinetic friction once moving:
(2)

Everyday Exmaple
Firefighter candidates must complete a physical ability test (PAT) that includes dragging a dummy across the floor. The PAT for the city of Lincoln Nebraska specifies that candidates must drag a human form dummy weighing 170 lbs for 25 feet, around a barrel, and then back across the starting point for a total distance of 50 feet in six minutes or less. The candidates may only drag the dummy using the pull harness attached to the dummy and cannot carry the dummy[3].
The test is held on a polished concrete floor. If a candidate pulls vertically up on the harness with a force of 70 lbs what horizontal pull force must the candidate apply in order to get the dummy moving? The static friction coefficient between cotton clothing and polished concrete is 0.5
The dummy will move if the candidate supplies anything more than the maximum static frictional force, so let’s try to calculate that.
If a candidate pulls vertically up on the harness with a force of 70 lbs then the floor must provide a normal force of 100 lbs to support the dummy. Now that we have the friction coefficient and normal force we can calculate the maximum static frictional force.

After the dummy starts moving, what force is required to keep it moving if  ?
?

Synovial Joint Friction
Static and kinetic friction are both present in joints. Static friction must be overcome, by either muscle tension or gravity, in order to move. Once moving, kinetic friction acts to oppose motion, cause wear on joint surfaces, generate thermal energy, and make the body less efficient. (We will examine the efficiency of the body later in this textbook.) The body uses various methods to decrease friction in joints, including synovial fluid, which serves as a lubricant to decrease the friction coefficient between bone surfaces in synovial joints (the majority of joints in the body). Bone surfaces in synovial joints are also covered with a layer of articular cartilage which acts with the synovial fluid to reduce friction and provides something other than the bone surface to wear away over time[4].

Synovial joints allow for smooth movements between the adjacent bones. The joint is surrounded by an articular capsule that defines a joint cavity filled with synovial fluid. The articulating surfaces of the bones are covered by a thin layer of articular cartilage. Ligaments support the joint by holding the bones together and resisting excess or abnormal joint motions. Image Credit: OpenStax Anatomy & Physiology
Check out the following lever simulation explore how force and distance from fulcrum each affect the equilibrium of the lever. This simulation includes the effects of friction, so you can see how kinetic friction works to stop motion and static friction contributes to maintaining static equilibrium.
https://openoregon.pressbooks.pub/bodyphysics/?p=473
The equations given for static and kinetic friction are empirical models that describe the behavior of the forces of friction. While these formulas are very useful for practical purposes, they do not have the status of laws or principles. In fact, there are cases for which these equations are not even good approximations. For instance, neither formula is accurate for surfaces that are well lubricated or sliding at high speeds. Unless specified, we will not be concerned with these exceptions.[5]
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Jul 11, 2018 [1]http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.18. ↵
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Aug 2, 2018 [2]http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@11.1. ↵
- "Firefighter Physical Ability Test Candidate Orientation Guide" by Industrial/Organizational Solutions, Inc.↵
- OpenStax, Anatomy & Physiology. OpenStax CNX. Jun 25, 2018 [3]http://cnx.org/contents/14fb4ad7-39a1-4eee-ab6e-3ef2482e3e22@10.1. ↵
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Aug 2, 2018 [4]http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@11.1. ↵


