11.7: Cotton Kills

Conduction

Cotton is a great thermal insulator – as long as it’s dry. Once wet, cotton becomes a poor insulator and does a poor job of preventing hypothermia-hence the old adage, “cotton kills”. To understand why cotton is sometimes good insulator and sometimes a poor one, we need to understand conduction, which is the transfer of thermal energy between objects by direct contact. The average kinetic energy of the molecules in a hot body is higher than in a colder body. If two molecules collide, an energy transfer from the molecule with greater kinetic energy to the molecule with less kinetic energy occurs. The cumulative effect from many collisions occurring at a surface of contact between the two objects results in transfer of heat from the hot object to the colder object, (or colder environment) in agreement with the Second Law of Thermodynamics.

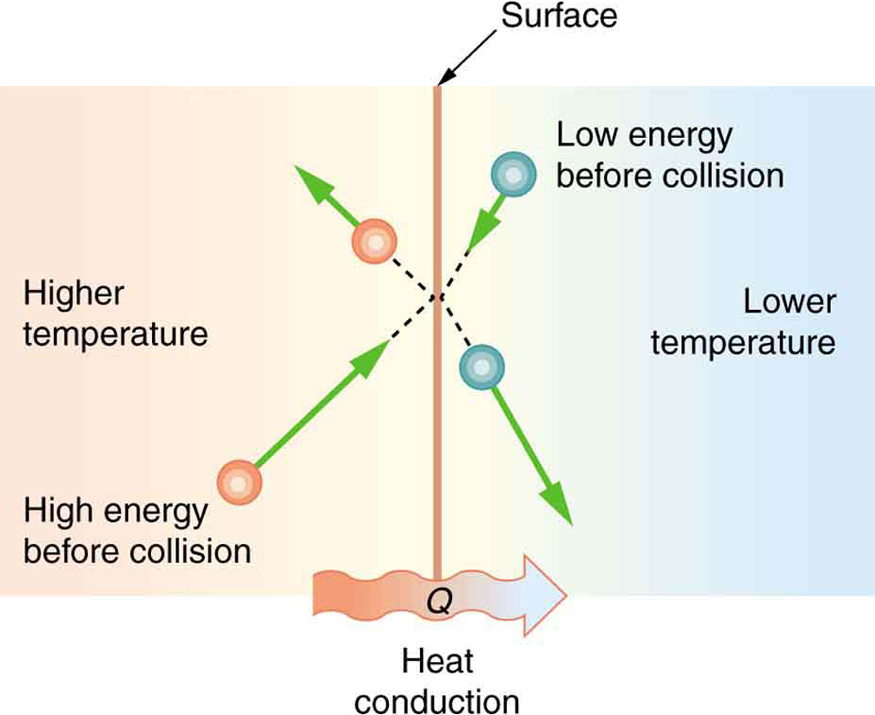
The molecules in two objects at different temperatures have different average kinetic energies. Collisions occurring at the contact surface tend to transfer energy from high-temperature regions to low-temperature regions, in agreement with the second Law of Thermodynamics. In this illustration, a molecule in the lower temperature region (right side) has low energy before collision, but its energy increases after colliding with the contact surface. In contrast, a molecule in the higher temperature region (left side) has high energy before collision, but its energy decreases after colliding with the contact surface.

Contact Area

The number of molecular collisions increases with increasing contact area (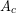), so the rate of heat conduction depends on the contact area. More collisions, and thus more time, will be needed to transfer the same amount of heat across a thicker material, so heat transfer rate also depends on thickness, or length across which the heat is transferred (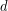). This model explains why thick clothing is warmer than thin clothing in winters, and why thin people are typically more susceptible to hypothermia.

Temperature Difference

If the object temperatures are the same, the net heat transfer rate falls to zero, and thermal equilibrium is achieved. As the difference in temperature increases, the average kinetic energy transferred from fast to slow molecules during each collision also increases. Therefore the temperature difference also affects the rate of heat transfer by conduction.

Thermal Conductivity

Lastly, some materials conduct thermal energy faster than others. In general, good conductors of electricity (metals like copper, aluminum, gold, and silver) are also good heat conductors, whereas insulators of electricity (wood, plastic, and rubber) are poor heat conductors. The effect of a material’s properties on conductive heat transfer rate is described by the coefficient of thermal conductivity (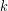), which is sometimes shortened to just thermal conductivity. The following table shows values of 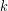for some common materials in units of Watts, per meter, per Kelvin ().

Thermal Conductivities of Common Substances

Substance	Thermal conductivity ()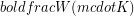
Silver	420
Copper	390
Gold	318
Aluminum	220
Steel iron	80
Steel (stainless)	14
Ice	2.2
Glass (average)	0.84
Concrete brick	0.84
Water	0.6
Fatty tissue (without blood)	0.2
Asbestos	0.16
Plasterboard	0.16
Wood	0.08–0.16
Snow (dry)	0.10
Cork	0.042
Glass wool	0.042
Wool	0.04
Down feathers	0.025
Air	0.023
Styrofoam	0.010

Conduction Equation

We can summarize all of the factors effecting the conductive heat transfer rate, which is an amount of energy transferred per time, in a single diagram:

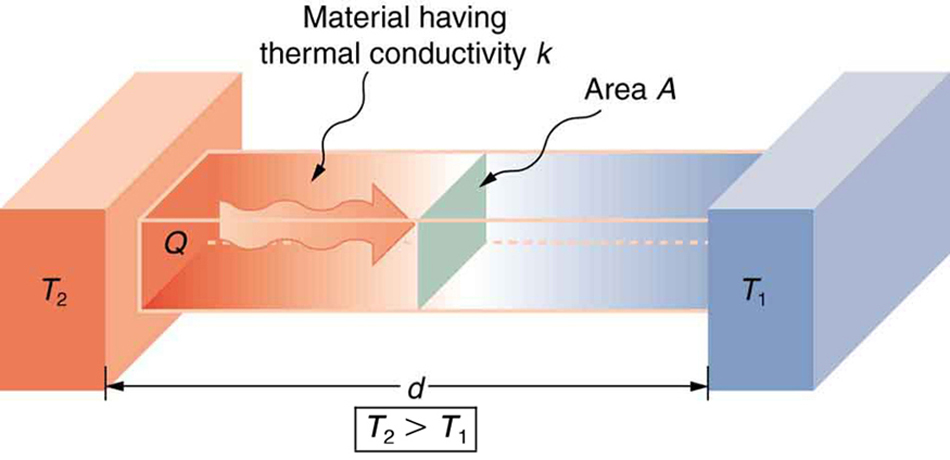
Heat conduction occurs through any material, represented here by a rectangular bar, whether window glass or walrus blubber. The temperature of the material is 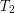on the left and 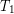on the right, where 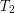is greater than 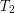. The rate of heat transfer by conduction is directly proportional to the surface area A, the temperature difference, and the substance’s conductivity k. The rate of heat transfer is inversely proportional to the thickness d.

The rate of heat transfer across a material with temperature 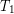on one side and temperature 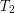on the other can be modeled by the conduction equation:

(1)

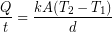
The rate of heat transfer ()refers to an amount of energy transferred per unit time so it has the same units as power (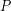). The term power is usually applied to a rate of transformation of energy from one form to another, but heat is a transfer of thermal energy from one place another, not a change in type of energy, thus we stick with 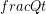instead of 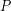as the notation for this rate. This notation also reminds us that if we want to know how much energy was transferred during a certain time, we need to multiply the heat rate by the time.

Insulation Technology

We can see from the conduction equation that combining thickness (loft) with low conductivity provides the greatest insulating effect. Goose down is the gold-standard insulation clothing for extreme-cold environments because it recovers loft after being compressed and it has low conductivity. As with most insulating materials, the effectiveness of down at reducing conduction is not due to the low conductivity of the feathers themselves, but rather their ability to trap air which has a very low conductivity. Double-pane windows, Styrofoam, animal hair, and the fiberglass insulation used in buildings all rely on this same strategy of trapping air to provide insulation.

The fiberglass batt is used for insulation of walls and ceilings to prevent heat transfer between the inside of the building and the outside environment.

Everyday Example: Down Insulation

Let’s compare the insulating properties of a cotton sweatshirt and a down jacket, such as the one worn in the photograph below.

The author approaches the summit of Mt. Washington in the Central Oregon Cascades, in snowstorm, but wearing a down jacket. February 2017.

We will start with the conduction equation:

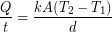
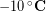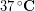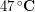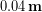The outside temperature was about and skin temperature is roughly , so the temperature difference was about . When dry, the down jacket pictured is roughly thick, which . The thermal conductivity of dry down is roughly 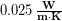. Using the methods in Chapter 17 we estimate the surface area of the upper body to be 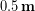. Entering these values into the equation we find:

So heat loss rate through the upper body in this situation is 30 W. That means 15 J of thermal energy is released to the environment as heat through the upper body each second. The typical human thermal power is 100 W so it appears that there is plenty of thermal energy available to maintain temperature. However, the 15 W value we found does not account for heat loss from the lower body, which we can see from the picture were not covered with down. In fact the single thin layer worn on the legs easily allowed for the other 85 W to escape so that body temperature was not elevated. In fact, doing the extra work of climbing the mountain likely raised the the thermal power closer to 300 W so actually something closer to 285 W was being exhausted through the lower body. As a result, body temperature dropped quickly when climbing stopped and the thermal power fell back to about 100 W.

If the down were to get wet, things would change drastically. The down would lose its loft and end up with roughly 0.5 cm thickness. Even worse, the water would fill in the air spaces between the down fibers so the thermal conductivity would essentially be the same as for water, which is 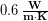. Entering these values into the conduction equation we find:

Now that’s a problem. The wet heat loss rate is nearly 190x faster than for the dry down in this situation, so to keep up we would need to eat 188 candy bars every six hours, or 31 candy bars per hour! Our bodies would not be able to digest and convert chemical potential energy to thermal energy fast enough to keep warm in that situation and eventually hypothermia would occur. Later in this unit we will be able to estimate how long it would take for the body temperature to drop to dangerous levels in this situation. Down is clearly a poor insulator when wet, but even after drying the fibers do not naturally recover their original loft. Down is a poor choice of insulation in wet environments, though it does well in snow storms as long as the air temperature is cool enough that the snow doesn’t melt when it lands on the jacket.

Everyday Examples: Cotton Kills

Just as with down, water can permeate the spaces between other fabrics like wool, synthetics, and cotton. The majority of water can be wrung out of wool and synthetics, partially restoring their insulating properties and helping them to dry out quickly and recover full insulation value. In the other hand, water fills space between cotton fibers and also saturates the fibers themselves. As a result cotton does not wring out well and dries slowly, so its thermal conductivity remains much closer to that of water than wool or synthetic. Cotton is a poor choice of insulation in wet environments.

Reinforcement Exercise: Single Pane Windows

Calculate the rate of heat loss through a window with dimensions 2 m x 3 m with thickness of 5 mm when the inside temperature is 22 °C and the outdoor temperature is 12 °C. Use the thermal conductivity of glass listed in the table found in this chapter.

Find the heat lost through the window in one day, in units of kW·hr, by first converting your answer to kilowatts (kW) and then multiply by 24 hours .

If electricity is $0.12 per kW·hr, how much money is spent each day to replace the heat loss from the window using and electric heater?

Significant content in this chapter, including the table of conductivities, was adapted from College Physics, by BC Open Textbooks ^[1]

---

1. "Conduction" by College Physics, BC Open Textbooks is licensed under CC BY 4.0↵