1.8: Projectile Motion

Learning Objectives

• Identify and explain the properties of a projectile, such as acceleration due to gravity, range, and trajectory.
• Apply the principle of independence of motion to solve projectile motion problems.

Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. The object is called a projectile, and its path is called its trajectory. The motion of falling objects is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this section, we consider two-dimensional projectile motion, such as that of a football or other object for which air resistance is negligible.

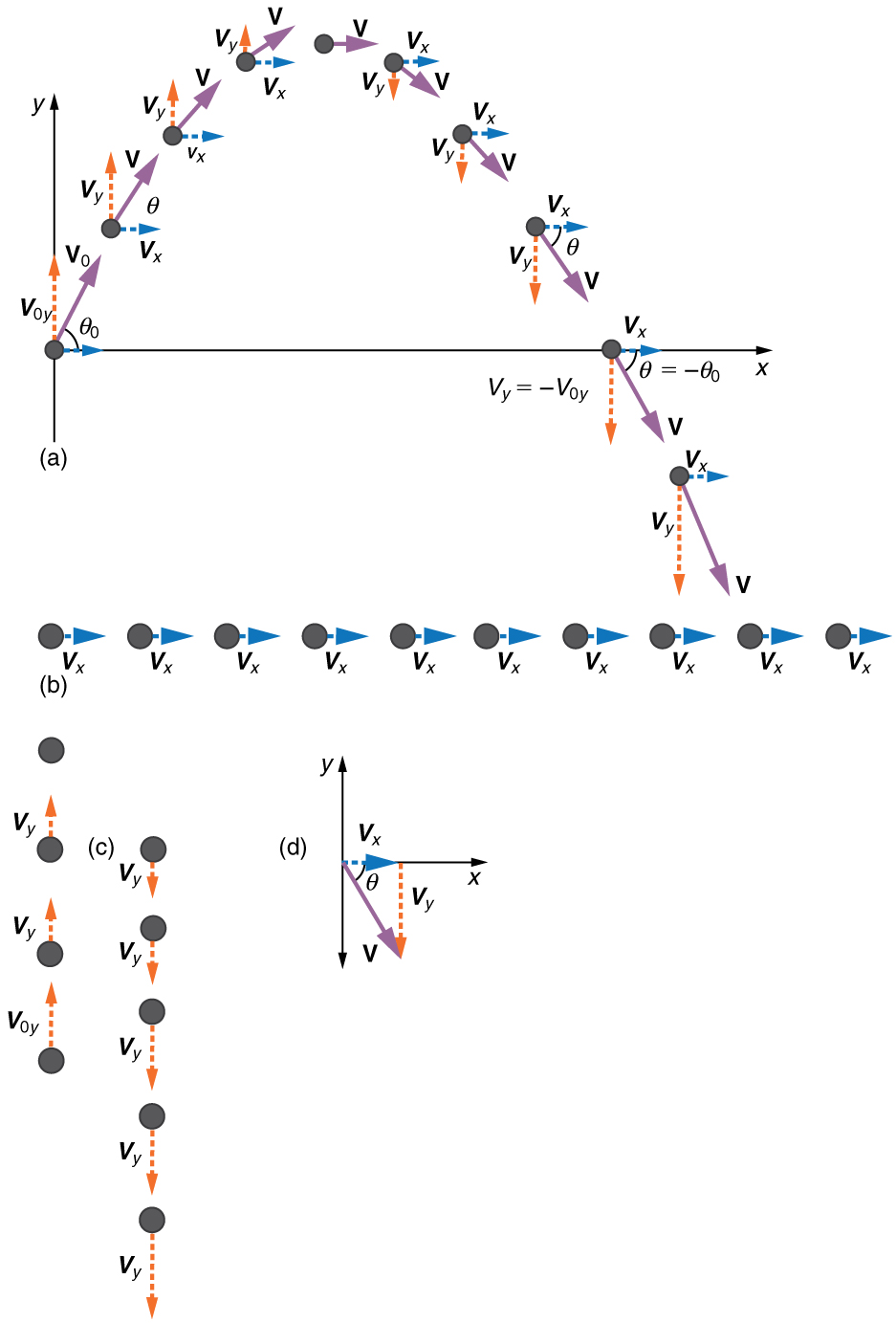
The most important fact to know here is that motions along perpendicular axes are independent and thus can be considered separately. In particular, it is often convenient to consider vertical and horizontal motions separately, or independently. The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. And we will assume all forces except gravity are negligible (that is, we ignore forces due to air resistance, wind, friction, etc.). The vertical component of acceleration is, then, \(a_{y}=-g=-9.80 \mathrm{~m} / \mathrm{s}^{2}\), where we take upward direction as the positive \(y\) direction. And because there is no force in the horizontal direction, \(a_{x}=0 \). Figure \(\PageIndex{1}\) illustrates this approach to analyzing projectile motion.

Figure \(\PageIndex{1}\): (a) We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. (b) The horizontal motion is simple, because \(a_{x}=0\) and \(v_{x}\) is thus constant. (c) The velocity in the vertical direction begins to decrease as the object rises; at its highest point, the vertical velocity is zero. As the object falls towards the Earth again, the vertical velocity increases again in magnitude. This is exactly same as in the case of falling objects (or objects thrown directly upward). (d) The x - and y -motions can be recombined to give the total velocity at any given point on the trajectory.

One of the conceptual aspects of projectile motion we can discuss without a detailed analysis is the range. On level ground, we define range to be the horizontal distance \(R\) traveled by a projectile. The range of projectiles describes everyday phenomena such as how far a football can be thrown or kicked. Also, investigating the range of projectiles can shed light on other interesting phenomena, such as the orbits of satellites around the Earth. Let us consider projectile range further.

Figure \(\PageIndex{2}\): Trajectories of projectiles on level ground. (a) The greater the initial speed \(v_{0}\), the greater the range for a given initial angle. (b) The effect of initial angle \(\theta_{0}\) on the range of a projectile with a given initial speed. Note that the range is the same for \(15^{\circ}\) and \(75^{\circ}\), although the maximum heights of those paths are different.

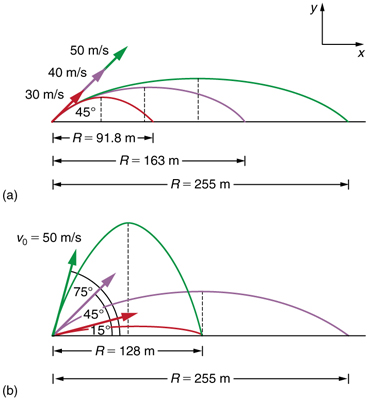
How does the initial velocity of a projectile affect its range? It is intuitive to guess that, the greater the initial speed \(v_{0}\), the greater the range, as shown in Figure \(\PageIndex{2}\) (a). The initial angle \(\theta_{0}\) also has a dramatic effect on the range, as illustrated in Figure \(\PageIndex{2}\) (b). For a fixed initial speed, such as might be produced by a cannon, the maximum range is obtained with \(\theta_{0}=45^{\circ} \). Interestingly, for every initial angle except \(45^{\circ}\), there are two angles that give the same range. The range also depends on the value of the acceleration of gravity \(g\). The lunar astronaut Alan Shepherd was able to drive a golf ball a great distance on the Moon because gravity is weaker there. The range \(R\) of a projectile on level ground for which air resistance is negligible is given by

\[R=\frac{v_{0}^{2} \sin 2 \theta_{0}}{g}, \nonumber\]

where \(v_{0}\) is the initial speed and \(\theta_{0}\) is the initial angle relative to the horizontal. This formula (which can be derived using algebra and trigonometry) fits the major features of projectile range as described.

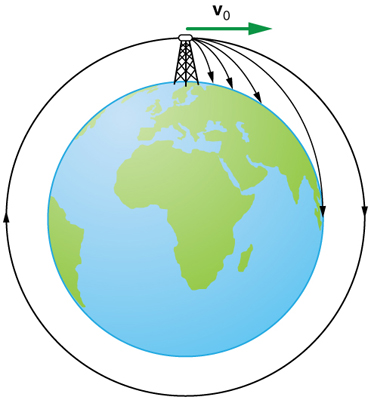
When we speak of the range of a projectile on level ground, we assume that \(R\) is very small compared with the circumference of the Earth. If, however, the range is large, the Earth curves away below the projectile and acceleration of gravity changes direction along the path. The range is larger than predicted by the range equation given above because the projectile has farther to fall than it would on level ground. (See Figure \(\PageIndex{3}\).) If the initial speed is great enough, the projectile goes into orbit. This possibility was recognized centuries before it could be accomplished. When an object is in orbit, the Earth curves away from underneath the object at the same rate as it falls. The object thus falls continuously but never hits the surface.

Figure \(\PageIndex{3}\): Projectile to satellite. In each case shown here, a projectile is launched from a very high tower to avoid air resistance. With increasing initial speed, the range increases and becomes longer than it would be on level ground because the Earth curves away underneath its path. With a large enough initial speed, orbit is achieved.

Summary

• Projectile motion is the motion of an object through the air that is subject only to the acceleration of gravity.
• The most important fact regarding projectile motion is that motions along vertical direction and the horizontal direction are independent.
• The maximum horizontal distance traveled by a projectile is called the range. The range \(R\) of a projectile on level ground launched at an angle \(\theta_{0}\) above the horizontal with initial speed \(v_{0}\) is given by

  \[R=\frac{v_{0}^{2} \sin 2 \theta_{0}}{g}. \nonumber\]

Glossary

centripetal acceleration

the acceleration of an object moving in a circle, directed toward the center

ultracentrifuge

a centrifuge optimized for spinning a rotor at very high speeds

uniform circular motion

an object moving in a circular path at constant speed