11.E: Light (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
12.4: The Electromagnetic Spectrum- Application Notes
1. If you live in a region that has a particular TV station, you can sometimes pick up some of its audio portion on your FM radio receiver. Explain how this is possible. Does it imply that TV audio is broadcast as FM?
2. Explain why people who have the lens of their eye removed because of cataracts are able to see low-frequency ultraviolet.
3. How do fluorescent soap residues make clothing look “brighter and whiter” in outdoor light? Would this be effective in candlelight?
4. Give an example of resonance in the reception of electromagnetic waves.
5. Illustrate that the size of details of an object that can be detected with electromagnetic waves is related to their wavelength, by comparing details observable with two different types (for example, radar and visible light or infrared and X-rays).
6. Why don’t buildings block radio waves as completely as they do visible light?
7. Make a list of some everyday objects and decide whether they are transparent or opaque to each of the types of electromagnetic waves.
8. Your friend says that more patterns and colors can be seen on the wings of birds if viewed in ultraviolet light. Would you agree with your friend? Explain your answer.
9. The rate at which information can be transmitted on an electromagnetic wave is proportional to the frequency of the wave. Is this consistent with the fact that laser telephone transmission at visible frequencies carries far more conversations per optical fiber than conventional electronic transmission in a wire? What is the implication for ELF radio communication with submarines?
10. Give an example of energy carried by an electromagnetic wave.
11. In an MRI scan, a higher magnetic field requires higher frequency radio waves to resonate with the nuclear type whose density and location is being imaged. What effect does going to a larger magnetic field have on the most efficient antenna to broadcast those radio waves? Does it favor a smaller or larger antenna?
12. Laser vision correction often uses an excimer laser that produces 193-nm electromagnetic radiation. This wavelength is extremely strongly absorbed by the cornea and ablates it in a manner that reshapes the cornea to correct vision defects. Explain how the strong absorption helps concentrate the energy in a thin layer and thus give greater accuracy in shaping the cornea. Also explain how this strong absorption limits damage to the lens and retina of the eye.
12.5: Reflection
13. Using the law of reflection, explain how powder takes the shine off of a person’s nose. What is the name of the optical effect?
12.6: Refraction
14. Diffusion by reflection from a rough surface is described in this chapter. Light can also be diffused by refraction. Describe how this occurs in a specific situation, such as light interacting with crushed ice.
15. Why is the index of refraction always greater than or equal to 1?
16. Does the fact that the light flash from lightning reaches you before its sound prove that the speed of light is extremely large or simply that it is greater than the speed of sound? Discuss how you could use this effect to get an estimate of the speed of light.
17. Will light change direction toward or away from the perpendicular when it goes from air to water? Water to glass? Glass to air?
18. Explain why an object in water always appears to be at a depth shallower than it actually is? Why do people sometimes sustain neck and spinal injuries when diving into unfamiliar ponds or waters?
19. Explain why a person’s legs appear very short when wading in a pool. Justify your explanation with a ray diagram showing the path of rays from the feet to the eye of an observer who is out of the water.
20. Why is the front surface of a thermometer curved as shown?
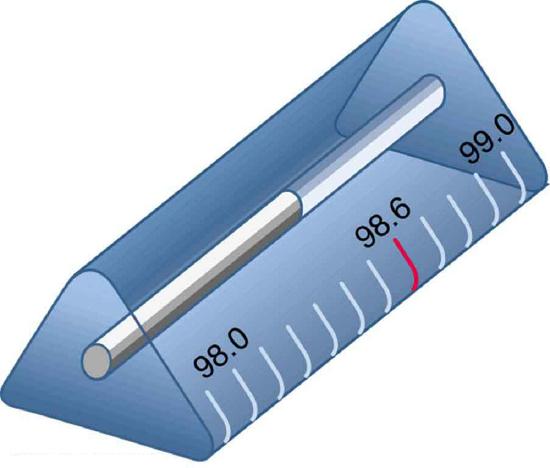
21. Suppose light were incident from air onto a material that had a negative index of refraction, say –1.3; where does the refracted light ray go?
12.8: Image Formation by Lenses
22. It can be argued that a flat piece of glass, such as in a window, is like a lens with an infinite focal length. If so, where does it form an image? That is, how are di and do related?
23. You can often see a reflection when looking at a sheet of glass, particularly if it is darker on the other side. Explain why you can often see a double image in such circumstances.
24. When you focus a camera, you adjust the distance of the lens from the film. If the camera lens acts like a thin lens, why can it not be a fixed distance from the film for both near and distant objects?
25. A thin lens has two focal points, one on either side, at equal distances from its center, and should behave the same for light entering from either side. Look through your eyeglasses (or those of a friend) backward and forward and comment on whether they are thin lenses.
26. Will the focal length of a lens change when it is submerged in water? Explain.
12.9: Image Formation by Mirrors
27. What are the differences between real and virtual images? How can you tell (by looking) whether an image formed by a single lens or mirror is real or virtual?
28. Can you see a virtual image? Can you photograph one? Can one be projected onto a screen with additional lenses or mirrors? Explain your responses.
29. Is it necessary to project a real image onto a screen for it to exist?
30. At what distance is an image always located—at do, di, or f?
31. Under what circumstances will an image be located at the focal point of a lens or mirror?
32. What is meant by a negative magnification? What is meant by a magnification that is less than 1 in magnitude?
33. Can a case 1 image be larger than the object even though its magnification is always negative? Explain.
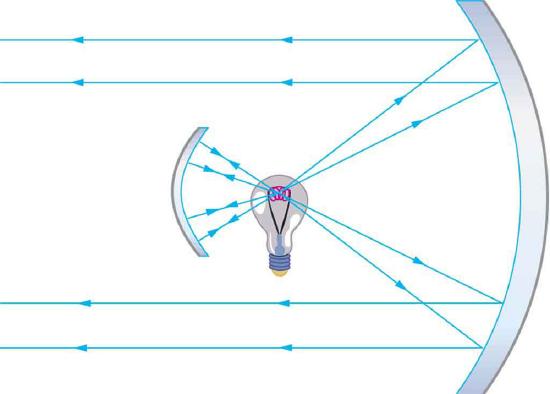
34. Figure 11.E.2 shows a light bulb between two mirrors. One mirror produces a beam of light with parallel rays; the other keeps light from escaping without being put into the beam. Where is the filament of the light in relation to the focal point or radius of curvature of each mirror?
35. Devise an arrangement of mirrors allowing you to see the back of your head. What is the minimum number of mirrors needed for this task?
36. If you wish to see your entire body in a flat mirror (from head to toe), how tall should the mirror be? Does its size depend upon your distance away from the mirror? Provide a sketch.
37. It can be argued that a flat mirror has an infinite focal length. If so, where does it form an image? That is, how are di and do related?
38. Why are diverging mirrors often used for rear-view mirrors in vehicles? What is the main disadvantage of using such a mirror compared with a flat one?
12.10: Polarization
39. Under what circumstances is the phase of light changed by reflection? Is the phase related to polarization?
40. Can a sound wave in air be polarized? Explain.
41. No light passes through two perfect polarizing filters with perpendicular axes. However, if a third polarizing filter is placed between the original two, some light can pass. Why is this? Under what circumstances does most of the light pass?
42. Explain what happens to the energy carried by light that it is dimmed by passing it through two crossed polarizing filters.
43. When particles scattering light are much smaller than its wavelength, the amount of scattering is proportional to 1/λ4. Does this mean there is more scattering for small λ than large λ? How does this relate to the fact that the sky is blue?
44. Using the information given in the preceding question, explain why sunsets are red.
Problems & Exercises
12.6: Refraction
45. What is the speed of light in water? In glycerine?
Solution
2.25×108 m/s in water
2.04×108 m/s in glycerine
46. What is the speed of light in air? In crown glass?
47. Calculate the index of refraction for a medium in which the speed of light is 2.012×108 m/s, and identify the most likely substance based on Table 12.6.1.
Solution
1.490, polystyrene
48. In what substance in Table 12.6.1 is the speed of light 2.290×108 m/s?
49. There was a major collision of an asteroid with the Moon in medieval times. It was described by monks at Canterbury Cathedral in England as a red glow on and around the Moon. How long after the asteroid hit the Moon, which is 3.84×105 km away, would the light first arrive on Earth?
Solution
1.28 s
50. Components of some computers communicate with each other through optical fibers having an index of refraction n=1.55. What time in nanoseconds is required for a signal to travel 0.200 m through such a fiber?
Solution
1.03 ns
51. On the Moon’s surface, lunar astronauts placed a corner reflector, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. What percent correction is needed to account for the delay in time due to the slowing of light in Earth’s atmosphere? Assume the distance to the Moon is precisely 3.84×108 m, and Earth’s atmosphere (which varies in density with altitude) is equivalent to a layer 30.0 km thick with a constant index of refraction n=1.000293.
12.7: Dispersion- The Rainbow and Prisms
52. (a) What is the ratio of the speed of red light to violet light in diamond, based on Table 12.7.1?
(b) What is this ratio in polystyrene?
(c) Which is more dispersive?


