6.12: Boundary Conditions
( \newcommand{\kernel}{\mathrm{null}\,}\)
We recall from Section 5.14, that, at a boundary between two media of different permittivities, the normal component of D and the tangential component of E are continuous, while the tangential component of D is proportional to ϵ and the normal component of E is inversely proportional to ϵ. The lines of electric force are refracted at a boundary in such a manner that
tanθ1tanθ2=ϵ1ϵ2.
The situation is similar with magnetic fields. That is, at a boundary between two media of different permeabilities, the normal component of B and the tangential component of H are continuous, while the tangential component of Bis proportional to m and the normal component of H is inversely proportional to μ. The lines of magnetic force are refracted at a boundary in such a manner that
tanθ1tanθ2=μ1μ2.
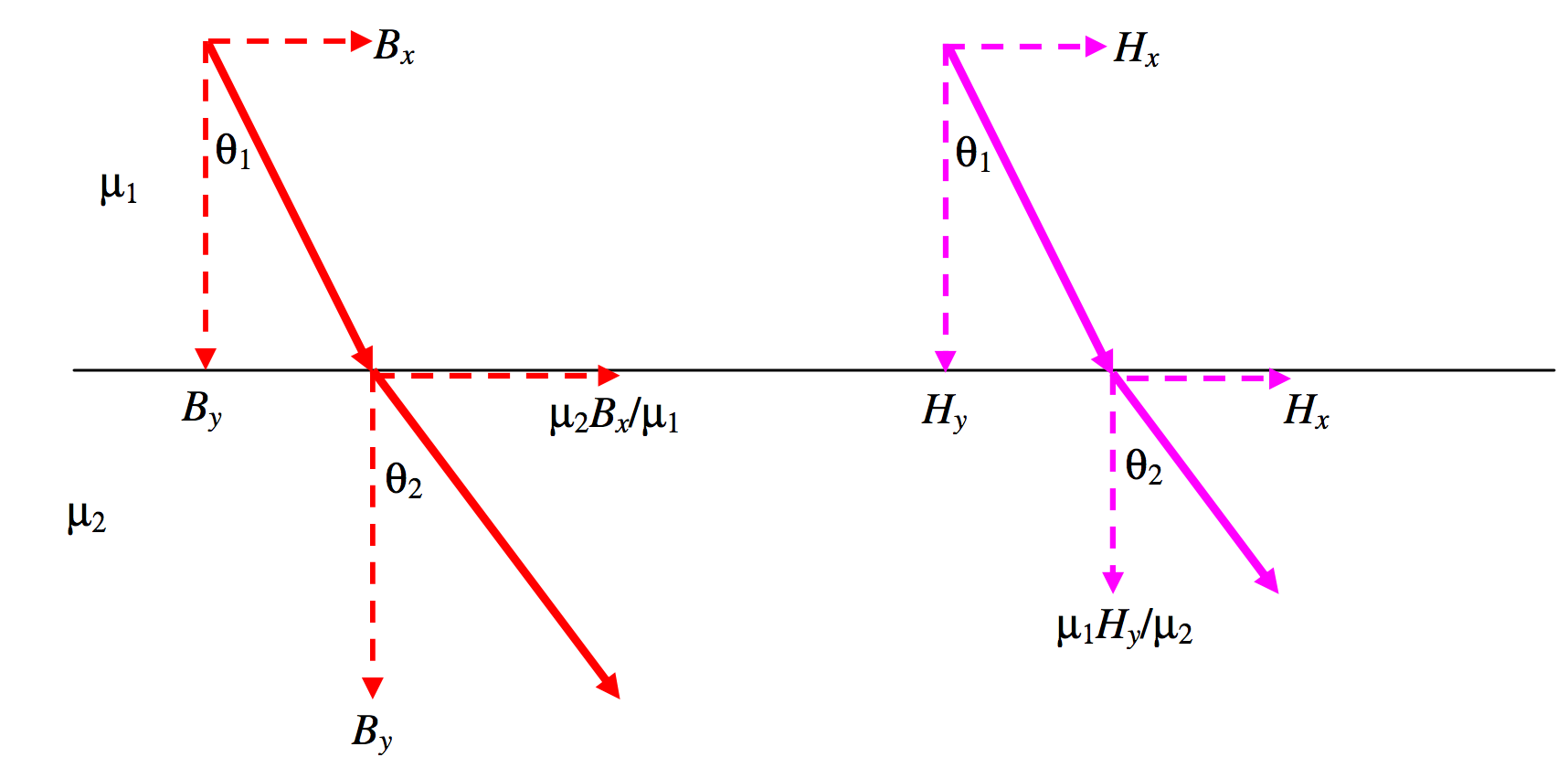
FIGURE VI.16
The configuration of the magnetic field inside an infinitely long solenoid with materials of different permeabilities needs some care. We shall be guided by the Biot-Savart law, namely B=μIdssinθ4πr, and Ampère’s law, namely that the line integral of H around a closed circuit is equal to the enclosed current. We also recall that the magnetic field inside an infinite solenoid containing a single homogeneous isotropic material is uniform, is parallel to the axis of the solenoid, and is given by H=nI or B=μnI.
The easiest two-material case to consider is that in which the two materials are arranged in parallel as in Figure VI.17.
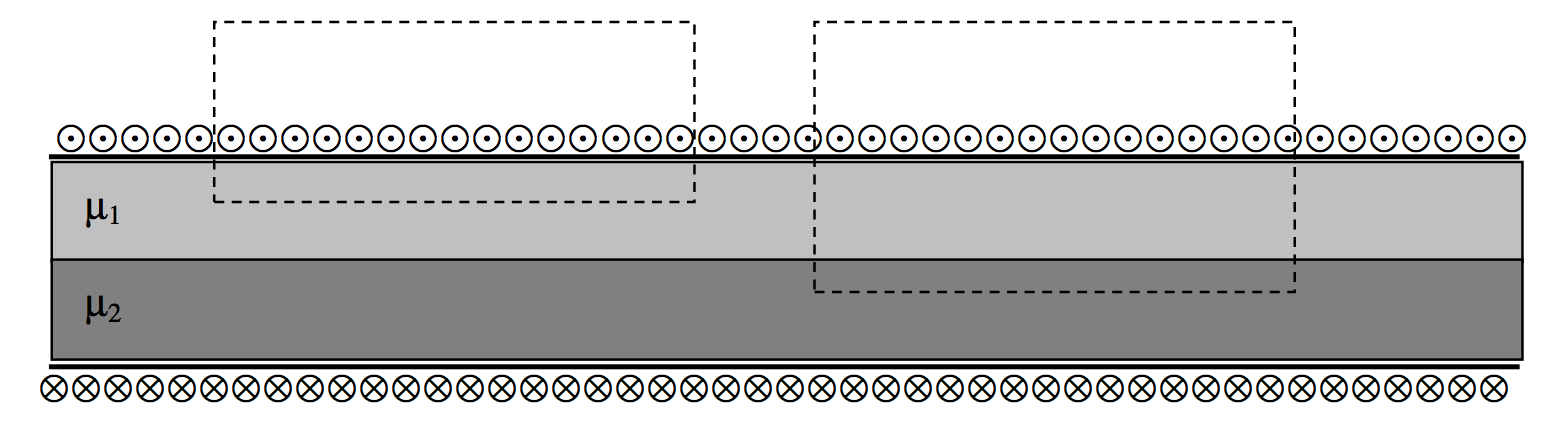
FIGURE VI.17
One can see by applying Ampère’s law to each of the two circuits indicated by dashed lines that the H-field is the same in each material and is equal to nI, and is uniform throughout the solenoid. It is directed parallel to the axis of the solenoid. That is, the tangential component of His continuous. The B-fields in the two materials, however, are different, being μ1nI in the upper material and μ2nI in the lower.
We now look at the situation in which the two materials are in series, as in Figure VI.18.
We’ll use a horizontal coordinate x, which is zero at the boundary, negative to the left of it, and positive to the right of it.
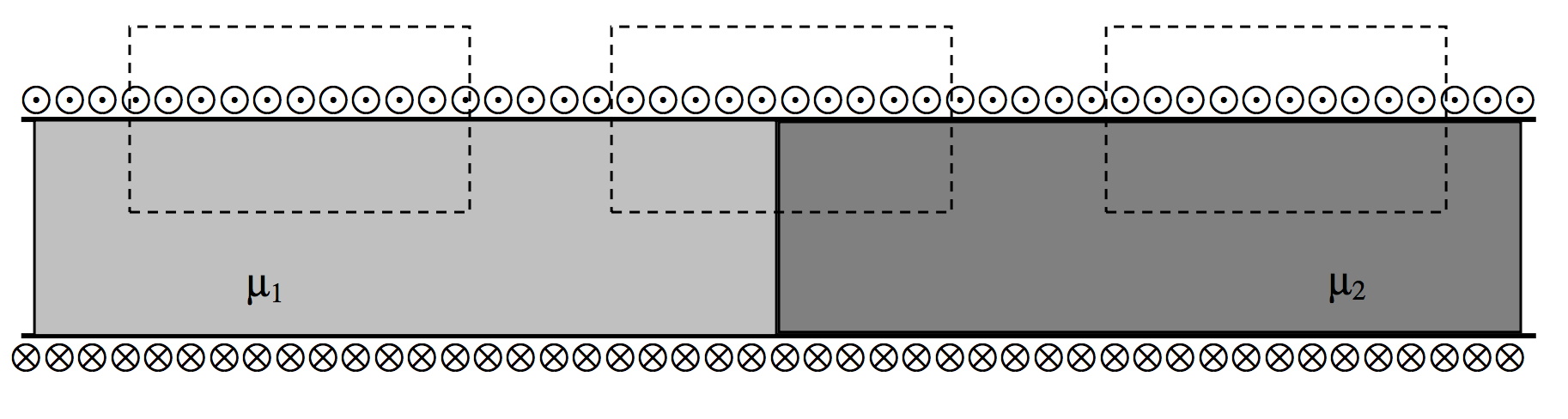
FIGURE VI.18
We might at first be tempted to suppose that B=μ1nI to the left of the boundary and B=μ2nI to the right of the boundary, while, by an application of Ampère’s law around any of the dashed circuits indicated, H=nI on both sides. Tempting though this is, it is not correct, and we shall see why shortly.
The B-field is indeed μ1nI a long way to the left of the boundary, and μ2nI a long way to the right. However, near to the boundary it is between these limiting values. We can calculate the B-field on the axis at the boundary by the same method that we used in Section 6.8. See especially equation 6.8, which, with the present geometry, becomes
B=12μ1nI∫0−π/2cosθdθ+12μ2nI∫π/20cosθdθ.
It should come as no surprise that this comes to
B=12(μ1+μ2)nI.
It is the same just to the left of the boundary and just to the right.
The H-field, however, drops suddenly at the boundary from 12(1+μ2μ1)nI immediately to the left of the boundary to 12(1+μ1μ2)nI immediately to the right of the boundary.
In any case, the very important results from these considerations is
- At a boundary between two media of different permeabilities, the parallel component of H is continuous, and the perpendicular component of B is continuous.
Compare and contrast this with the electrical case:
- At a boundary between two media of different permittivities, the parallel component of E is continuous, and the perpendicular component of D is continuous.


