5.7: Delta-Star Transform

As we did with resistors in Section 4.12, we can make a delta-star transform with capacitors.

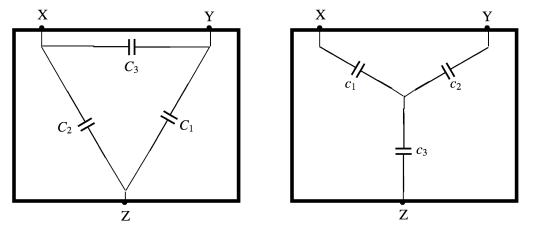
$\text{FIGURE V.7}$

I leave it to the reader to show that the capacitance between any two terminals in the left hand box is the same as the capacitance between the corresponding two terminals in the right hand box provided that

$$c_1=\frac{C_2C_3+C_3C_1+C_1C_2}{C_1},\label{5.7.1}$$

$$c_2=\frac{C_2C_3+C_3C_1+C_1C_2}{C_2},\label{5.7.2}$$

$$c_3=\frac{C_2C_3+C_3C_1+C_1C_2}{C_3},\label{5.7.3}$$

The converse relations are

$$C_1=\frac{c_2c_3}{c_1+c_2+c_3},\label{5.7.4}$$

$$C_2=\frac{c_3c_1}{c_1+c_2+c_3},\label{5.7.5}$$

$$C_3=\frac{c_1c_2}{c_1+c_2+c_3},\label{5.7.6}$$

For example, just for fun, what is the capacitance between points A and B in Figure $V.8$, in which I have marked the individual capacitances in microfarads?

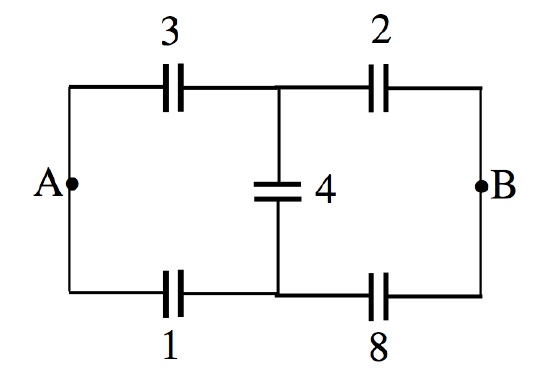
$\text{FIGURE V.8}$

The first three capacitors are connected in delta. Replace them by their equivalent star configuration. After that it should be straightforward. I make the answer 2.515 $\mu F$.