5.13: Sharing a Charge Between Two Capacitors
( \newcommand{\kernel}{\mathrm{null}\,}\)
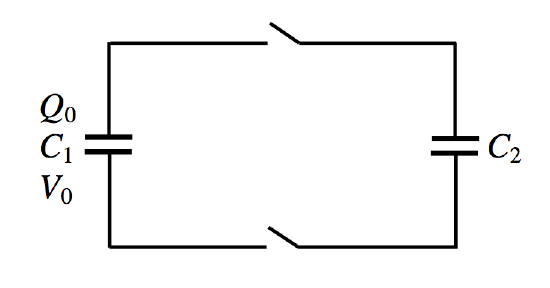
FIGURE V.14
We have two capacitors. C2 is initially uncharged. Initially, C1 bears a charge Q0 and the potential difference across its plates is V0, such that
Q0=C1V0,
and the energy of the system is
U0=12C1V20.
We now close the switches, so that the charge is shared between the two capacitors:

FIGURE V.15
The capacitors C1 and C2 now bear charges Q1 and Q2 such that Q0=Q1+Q2 and
Q1=C1C1+C2Q0 and Q2=C2C1+C2Q0.
The potential difference across the plates of either capacitor is, of course, the same, so we can call it V without a subscript, and it is easily seen, by applying Q=CV to either capacitor, that
V=C1C1+C2V0.
We can now apply U=12CV2 to each capacitor in turn to find the energy stored in each. We find for the energies stored in the two capacitors:
U1=C31V202(C1+C2)2 and U2=C2C21V202(C1+C2)2.
The total energy stored in the two capacitors is the sum of these, which is
U=C21V202(C1+C2),
which can also be written
U=C1C1+C2U0.
Surprise, surprise! The energy stored in the two capacitors is less than the energy that was originally stored in C1. What has happened to the lost energy?
A perfectly reasonable and not incorrect answer is that it has been dissipated as heat in the connecting wires as current flowed from one capacitor to the other. However, it has been found in low temperature physics that if you immerse certain metals in liquid helium they lose all electrical resistance and they become superconductive. So, let us connect the capacitors with superconducting wires. Then there is no dissipation of energy as heat in the wires – so the question remains: where has the missing energy gone?
Well, perhaps the dielectric medium in the capacitors is heated? Again this seems like a perfectly reasonable and probably not entirely incorrect answer. However, my capacitors have a vacuum between the plates, and are connected by superconducting wires, so that no heat is generated either in the dielectric or in the wires. Where has that energy gone?
This will have to remain a mystery for the time being, and a topic for lunchtime conversation. In a later chapter I shall suggest another explanation.


