1.2: 1.2 The Exponential Function
( \newcommand{\kernel}{\mathrm{null}\,}\)
The exponential function, denoted by “exp”, is one of the most important functions in mathematics. We will deal with it numerous times, in many different contexts.
To motivate its definition, let us start by thinking about what it means to take a number x to the power of y:
f(x)=xy.
For values of y in the natural numbers N≡{1,2,3,…}, the power operation simply means multiplying x by itself y times. For example, x4=x⋅x⋅x⋅x. But what about non natural number powers, like x−1 or x1/2 or xπ?
To help answer this question, we define the exponential function as the following limiting infinite series: exp(x)≡1+∞∑n=1xnn!,forx∈R.
Note
Note that the infinite series in this definition uses natural number powers only.
The exponential function’s domain is the set of real numbers, R, and its range is the set of positive numbers, R+.
Here is a graph of the function:
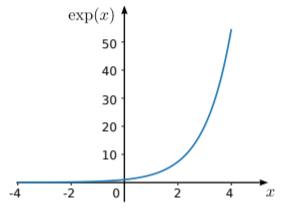
The exponential has several noteworthy features:
- The value of exp(x) increases extremely quickly with increasing x. Going in the other direction, the value approaches zero very quickly with decreasing x.
- exp(0)=1. (This follows from the definition of the exponential.)
- For all x,y∈R, exp(x+y)=exp(x)exp(y). Try proving this as an exercise (see Section 1.8). The key ingredients for the proof are (i) the above definition of the exponential and (ii) the binomial theorem.
- As a corollary of properties 2 and 3, exp(−x)=1/exp(x).


