1.3: 1.3 The Logarithm Function

Last updated
Save as PDF

Page ID: 34512

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Since the exponential is a one-to-one function, its inverse is a well-defined function. We call this the natural logarithm: \[\label{eq:1}\ln(x) \equiv y \;\; \mathrm{such}~\mathrm{that}\; \exp(y) = x.\] For brevity, we will henceforth use “logarithm” to refer to the natural logarithm, unless otherwise stated (the “non-natural” logarithms are not our concern in this course). The domain of the logarithm is \(y \in \mathbb{R}^+\), and its range is \(\mathbb{R}\). Its graph is shown below:

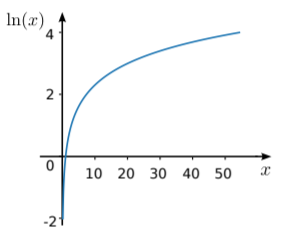
Observe that the graph increases extremely slowly with \(x\), precisely the opposite of the exponential’s behavior.

Using Eq. (1.2.3), we can prove that the logarithm satisfies the product and quotient rules \[\begin{align} \ln(xy) &= \ln(x) + \ln(y) \\ \ln(x/y) &= \ln(x) - \ln(y).\end{align}\]