Mirror Symmetry

Introduction

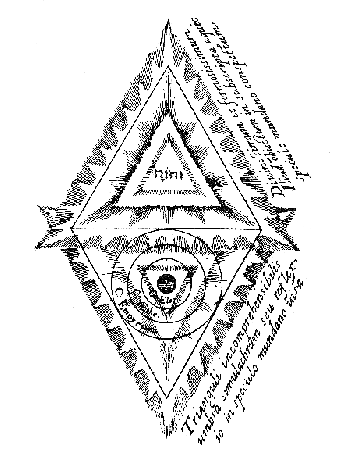The image to the right is a depiction of the universe as a mirror image of God, drawn by Robert Fludd in the early 17^th century.

The caption of the upper triangle reads: “That most divine and beautiful counterpart visible below in the flowing image of the universe.”

The caption of the lower triangle is: "A shadow, likeness, or reflection of the insubstantial triangle visible in the image of the universe.”

Symmetry

"A thing is symmetrical if there is something you can do to it so that after you have finished doing it it looks the same as before" -- Weyl

Example: a square under rotations of 90 degrees.

This is a rather strange definition: it says that a change equals no change.

Some symmetries of physical laws:

• Space translation. If I have some apparatus, and move it to a different place it will work the same. The laws governing its behavior are the same under space translation.
• Time translation. The apparatus works the same tomorrow as it does today.
• Rotation. If I rotate the apparatus is still works the same way.
• Mirror symmetry. If I build the mirror image of an apparatus, it works the same albeit in a mirrored way. Warning: below we shall see violations of this symmetry.

Why Do Mirrors Reverse Left and Right, Not Up and Down?

We say that mirrors reverse left and right. However, face a mirror and hold up your right hand. The hand that is raised in the mirror image of you is also on your right side. So what is it that is being reversed in a mirror image? Well, if the person you see in the mirror were real, you would say that the person is raising their left hand.

We imagine that we write a name on a fairly thin piece of paper, as shown.

We hold the sign up to a mirror. To the left is the sign, to the right is what we see in the mirror.

We see that left and right are apparently reversed, but not up and down.

Is this because we are looking with two eyes that are aligned horizontally, our left eye and our right one? No, because if we look with only one eye, it still looks the same.

We can explore this a little further by constructing a round disc. We cut a hole in the middle that we can look through, and we draw four F's on the disc. The sign is shown to the below.

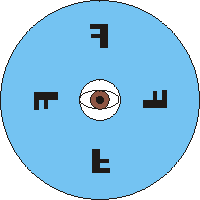
We hold the sign up to a mirror and look through the hole. What we see is shown to the right. All the F's are now a mirror image.

What if we hold the sign with the name on it de down? The mirror still reverses left and right, not up and down. The figure shows the upside down sign to the left, and the mirror image to the right.

You may need to look at these figures upside down to convince yourself that the original on the left "reads" the name while the mirror image does not.

Now we position the sign right side up and hold it up to a light and look through it from the back. We see the text in a mirror image! So if we hold the sign up to the mirror, what we see in the mirror looks like what we see looking through the sign from the back.

Now we take the sign, still looking at it from behind, and pull the left and right edges towards us. What we see is the image on the left. The left and right edges of the sign curve towards us.

We hold the bent sign up to the mirror and peek over it at the mirror. The text in the mirror image, shown to the right, is still mirror reversed. But, in the mirror image the left and right edges of the sign are curving away from us!

Now we begin to understand that it is front and back that are being reversed by the mirror. The original has the left and right edges of the sign curving towards us, while in the mirror the left and right edges curve away from us.

A further subtlety is that in some sense the surface that we see in the mirror is the surface that we see when we look directly at an object, but we are looking at it from inside!

For some reason this circumstance and the surrounding confusion reminds me of a famous painting by Salvador Dali titled "Exploding Head in the Style of Rafael."

Weak Interactions and Mirror Symmetry

You will recall that we can classify the world in terms of the interactions that occur between objects. The current list is:

1. Strong interaction. This is the interaction that holds the nucleus together.
2. Weak interaction. This is responsible for radioactive decay.
3. Electromagnetic. The interaction between electrically charged bodies.
4. Gravitation. The interaction between objects which have mass.

Sometimes I think the chemical covalent bond deserves a place on the list, but for now we shall use the conventional list of four types of interaction.

As you probably know, it used to be thought that the electric interaction and the magnetic interaction were separate. They were unified in the nineteenth century by Faraday and Maxwell. We shall discuss further unification in the above list later in the term.

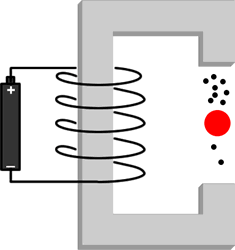
In 1956 physicists Chen Ning Yang and Tsung Dao Lee realised that although mirror symmetry had been shown to be true for the strong, electromagnetic and gravitational interactions, they believed that it had never been tested for the weak interaction. Madame Chien-Shiung Wu did an experiment to test mirror symmetry for weak interactions. A schematic of her apparatus is shown to the right. A sample of radioactive Cobalt-60 is emitting electrons by radioactive decay; the Cobalt-60 is placed between the poles of an electromagnet and most of the electrons are drawn down towards the upper pole of the magnet.

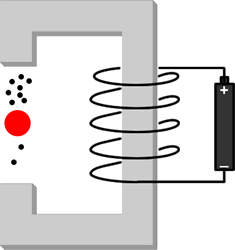
The figure to the right is just the mirror image of the previous one. Note that there is no sequence of rotations and translations that will turn the upper figure into the one to the right: the way the coil of wire is wound around the iron of the electromagnet will always come out wrong.

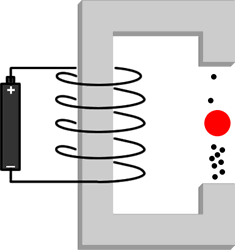
But, if one constructs a mirror image of the apparatus the result is not the above figure. Now the electrons are being drawn to the lower pole of the magnet. Thus we see that mirror symmetry is not true for weak interactions.

If the mechanism inside the red sphere that produces the electrons were anything other than the weak interaction, this figure would not be correct: instead the previous figure would be the experimental result.

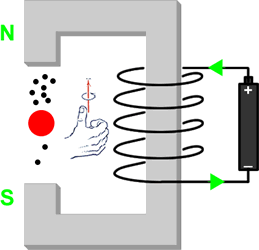
Although explaining what has happened to cause this violation of mirror symmetry is not crucial for our purposes, the figures to the right indicate what has happened. We have added some labels (in green for those viewing this in color); note that these labels are for our purposes only and are not part of the apparatus. We show the direction of the current in the wires, and have labeled the poles of the magnet. In both cases the electrons are being drawn to the North Pole of the magnet. In the mirror image, the helicity of the coil of wire has been changed, which changes the polarity of the magnet.

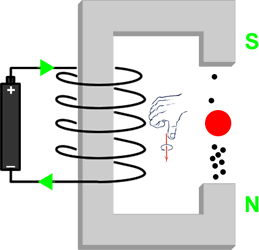
We can go a bit further by using a right hand rule. If we curl the fingers of our right hand in the direction of the flow of the current in the coil of wire, in the upper case our thumb will point up, while for the lower arrangement our thumb points down.

The technical phrase for the above result, which we shall seldom if ever use, is that the weak interaction violates conservation of parity.

So, if we construct some apparatus that is based on the weak interaction, an apparatus constructed as a mirror image will work differently. This was a great shock to physicists.

Technical Note

The above schematics of Madame Wu's apparatus can be a bit mis-leading. First, the magnetic field must be very strong, and therefore the source of the current for the electromagnetic must be a very powerful power supply, not a simple battery such as is shown in the figure. Second, the Cobalt-60 source must be cooled to a very low temperature.

Life Also Violates Mirror Symmetry

We know that our bodies are only roughly symmetric. Our heart is on the left, our liver on the right. The two lobes of the brain process different sorts of information.

Taking a photograph of the face of someone you know and replacing the right half of the face with a mirror image of the left can alter the appearance dramatically: our faces are not completely symmetric either. The figure to the right illustrates with the author of this document.

A similar study of other faces is available here.

This violation of mirror symmetry occurs down to the molecular level. For example, the amino acid alanine, one of the components of DNA, exists in two mirror image forms. The chemical groups shown below lie on the vertices of a tetrahedron. Note that there is no combination of rotations and translations that can turn the form on the left into the form on the right.

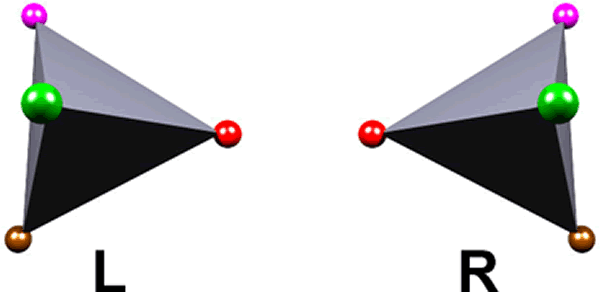
The legend for the figure appears to the right. It turns out that the only type of alanine found in living creatures is the form on the left. Most other basic biological molecules that are different from their mirror images similarly only exist in one form in living creatures.

Is there any relation between the violation of mirror symmetry for weak interactions and the violation of mirror symmetry for life? Possibly.

As you may know, if one puts together a "soup" of carbon, water, a little nitrogen, etc. and zaps it with a high-voltage electrical arc, amino acids and other simple building blocks of life are formed. The speculation is that the "soup" could have existed in the early days of the Earth and the zap corresponds to a lightning strike. Thus we may see how these molecules were originally formed.

In the experiment, though, equal amounts of the L and R forms of the molecules are created.

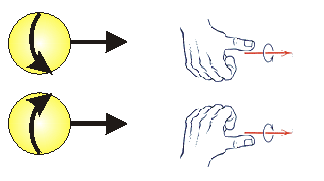One type of "cosmic ray" is actually electrons that are released when Carbon-14 in the upper atmosphere radioactively decays into Nitrogen-14. The Carbon-14 is produced in the upper atmosphere due to solar radiation. As we will be discussing in great detail later, all electrons have what we call spin. If an electron is moving to the right, as shown, there are two possible relations between the velocity and the orientation of the spin. But, because the weak interaction that caused these electrons violates mirror symmetry, only the upper "helicity" state exists in cosmic rays.

As shown in the above figure, the two helicity states correspond to different handedness. If the fingers of the right hand curl in the direction of the spin, the thumb points in the direction of motion for the upper electron. For the lower electron it is the left hand that defines the helicity.

Note that this further explains Madame Wu's experiment: the electrons' helicity interacts with the magnetic field to draw them to the North Pole of the magnet. Any mechanism other than the weak interaction that produces electrons will produce them in equal helicity states. In such a case, the electrons will be drawn equally to the North and South poles of the magnet and mirror symmetry will be preserved.

These cosmic rays tend to destroy amino acids. In the laboratory, if the soup containing amino acids etc. is exposed to electrons of the helicity found in cosmic rays the R form of alanine, for example, is preferentially destroyed. Thus we end up with an excess of the "correct" kind of molecules, the type found in living creatures.

Thus the violation of mirror symmetry in weak interactions can break the symmetry in the molecules found in living creatures. This could conceivably later lead to the large-scale violations in mirror symmetry we see in living creatures.

About "Crucial Experiments"

Above I mentioned that in 1956 Lee and Yang believed that mirror symmetry had never been tested for weak interactions. They won a Nobel Prize in Physics for this work.

It turns out that in their search they missed two articles:

1. R.T. Cox, C.G. McIlwraith and B. Kurrelmeyer, 'Apparent Evidence of Polarisation in a Beam of Beta-Rays', Proceedings of the National Academy of Sciences 14, (1928) pg. 544.
2. C.T. Chase, 'The Scattering of Fast Electrons by Metals II. Polarisation of Back Scattering at Right Angles' Physical Review 36, (1930) pg. 1060.

Both of these papers, published in two very prestigious journals, provided strong evidence that mirror symmetry does not hold for weak interactions. But when Lee and Yang attempted to review all the available evidence they missed both of these papers.

How can this be?

It turns out that pretty well everybody missed these papers.

The problem may be that in the late 1920's and early 1930's the current state of theoretical physics did not allow even thinking about this problem in the way that we have discussed it above. Thus these experiments were outside the scope of the physics thinking of the day, which may well be why the papers were almost universally ignored.

You may learn more about the issue of crucial experiments from: Gerald Holton, 'Einstein, Michelson, and the "Crucial" Experiment' Isis 60, (1960) pg. 133. The essay is also reprinted in Gerald Holton, Thematic Origins of Scientific Thought (Harvard, 1973).