1.10: Reflection and Transmission at an Interface

When an electromagnetic field is incident on an interface between different media, the field is partially reflected and partially transmitted. An important special case is that of a monochromatic plane wave which is incident on a planar interface as in Figure \(\PageIndex{2}\).

Let the interface be the plane \(z = 0\) between materials in \(z < 0\) and \(z > 0\) with permittivities \(E_i\) and \(E_t\), respectively. We first assume that the materials are lossless, i.e. that the permittivities are real. The plane wave is incident from medium \(z < 0\) and the incident electromagnetic field is given by:

\[ \begin{align} ε^i(r, t) &= Re [ ε^i(r)e^{−iωt}] \\[4pt] &= Re \left[ A^ie^{i(k^{i}·r−ωt)}\right] \end{align} \nonumber \]

and

\[\begin{align} H^i(r, t) &= Re [ H^i(r)e^{−iωt}] \\[4pt] &= Re \left[ \dfrac{k^i}{ωµ_{0}} × A^ie^{i(k^{i}·r−ωt)}\right] \end{align} \nonumber \]

where kⁱ = kⁱ_xx + kⁱ_yy + kⁱ_zz, with

\[k_{z}^i=(k_{0}^2E_{i} − (k_{x}^i)^2 − (k_{y}^i)^2)^{1/2}. \nonumber \]

Because the time dependence is given by \(\exp(−iωt)\) with \(ω > 0\) and the incident wave propagates in the positive z-direction, the positive square root is chosen for kⁱ_z . Part of the incident field is reflected into \(z < 0\) and part is transmitted into \(z > 0\). The reflected field is written as

\[ε^r(r, t) = Re [ ε^r(r)e^{−iωt}] = Re [ A^re^{i(k^{r}·r−ωt)}] , \nonumber \]

\[H^r(r, t) = Re [ H^r(r)e^{−iωt}] = Re [ \dfrac{k^r}{ωµ_{0}} × A^re^{i(k^{r}·r−ωt)}] , \nonumber \]

where k^r = k^r_xx + k^r_yy + k^r_zz, with

\[k_{z}^r=(k_{0}^2E_{i} − (k_{x}^r)^2 − (k_{y}^r)^2)^{1/2}, \nonumber \]

where the minus sign is chosen because the reflected wave propagates in the negative z-direction. The transmitted field is for \(z > 0\)

\[ε^t(r, t) = Re [ ε^t(r)e^{−iωt}] = Re [ A^te^{i(k^{t}·r−ωt)}] , \nonumber \]

\[H^t(r, t) = Re [ H^t(r)e^{−iωt}] = Re [ \dfrac{k^t}{ωµ_{0}} × A^te^{i(k^{t}·r−ωt)}] , \nonumber \]

where k^t = k^t_xx + k^t_yy + k^t_zz, with

\[k_{z}^t=(k_{0}^2E_{i} − (k_{x}^t)^2 − (k_{y}^t)^2)^{1/2}. \nonumber \]

Our aim is to determine A^r and A^t for given Aⁱ.

1.9.1 Boundary Conditions at an Interface

There exist conditions for the continuity of the tangential and the normal components of both the electric and magnetic fields at an interface between different media. The boundary conditions for the tangential components follow from the Maxwell equations that contain the curl-operator, i.e. (1.6.2) and (1.6.3). There holds for the interface z = 0 with the incident, reflected and transmitted plane waves introduced above:

\[\hat{z} × (E^i + E^r ) = \hat{z} × E^t, \nonumber \]

\[\hat{z} × (H^i + H^r ) = \hat{z} × H^t, \nonumber \]

where z is the unit normal on the interface. This means that the tangential components of the total electric and total magnetic field are continuous across the interface, or explicitly:

\[E_{x}^i(x, y, 0) + E_{x}^r(x, y, 0) = E_{x}^t(x, y, 0), \nonumber \]

\[E_{y}^i(x, y, 0) + E_{y}^r(x, y, 0) = E_{y}^t(x, y, 0), \nonumber \]

and similarly for the magnetic field.

Figure \(\PageIndex{1}\): Closed loop in the (x, z)-plane enclosing the area A and surrounding part of the interface z = 0, as used in Stokes’ Law to derive the continuity of the electric and magnetic components which are tangential to the interface and parallel to the plane through the loop.

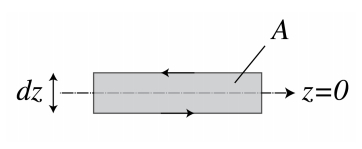
We will only demonstrate the continuity of the tangential components for the electric field. By choosing a closed loop in the (x, z)-plane which is intersected by the interface z = 0 as shown in Figure \(\PageIndex{1}\), and integrating the y-component of Faraday’s Law (1.3.12) for the total electromagnetic field over the area A bounded by the loop L, we obtain:

\[-µ_{0}\dfrac{d}{dt}\iint\limits_{A} \hat{y}H\, dA=\iint\limits_{A} \hat{y}∇ × ε\, dA=\oint\limits_{L} ε\, dl \nonumber \]

where in the last step we used Stokes’ theorem with the direction of integration over the loop given by that of the direction of rotation of screw driver when it moves in the direction of the normal y. In words: the rate of change of the magnetic flux through the surface A is equal to the integral of the tangential electric field over the bounding closed loop L.

By taking the limit dz → 0, the surface integral and the integrals over the vertical parts of the loop vanish and there remain only the integrals of the tangential electric field over the horizontal parts of the loop on both sides of the interface z = 0. Since these integrals are traversed in opposite directions and the lengths of these parts are the same and arbitrary, we conclude for the loop as shown in Figure \(\PageIndex{1}\) that

\[lim_{z↑0} ε_{x}(x, y, z, t) = lim_{z↓0} ε_{x}(x, y, z, t), \nonumber \]

where ε is the total electric field, i.e. it is equal to the sum of the incident and the reflected field for z < 0, and equal to the transmitted field in z > 0. By choosing the closed loop in the (y, z)-plane instead of the (x, z)-plane one finds similarly that the y-component of the electric field is continuous. The continuity of the tangential components of the magnetic field are derived in a similar manner.

Our derivation holds for electromagnetic fields of arbitrary time dependence. Furthermore, the derivation used above for the planar interface z = 0 can easily be generalized for curved surfaces. Therefore we conclude:

The tangential electric and magnetic field components are continuous across any interface.

By integrating Maxwell’s equations that contain the div-operator (1.3.14), (1.3.15) over a pill box with height dz and top and bottom surfaces on either side and parallel to the interface, and considering the limit dz → 0, we find continuity relations for the normal components of the fields:

\[lim_{z↑0} E_{i}\hat{z}ε_{x}(x, y, z, t) = lim_{z↓0} E_{t}\hat{z}εx(x, y, z, t), \nonumber \]

\[lim_{z↑0} H_{x}(x, y, z, t) = lim_{z↓0} H_{x}(x, y, z, t), \nonumber \]

The normal components of Eε and H are continuous across an interface.

Remark

Since all derived boundary conditions hold for all times t, it follows that for timeharmonic fields they also hold for the complex fields. Hence (\(\PageIndex{10}\)) and (\(\PageIndex{11}\)) hold and similarly we find that the normal components of Eε and H are continuous.

1.9.2 Snell’s Law

By substituting the complex electric fields derived from (\(\PageIndex{1}\)), (\(\PageIndex{4}\)) and (\(\PageIndex{7}\)) into equation (\(\PageIndex{10}\)), we get

\[\hat{z} × [A^ie^{i(k_{x}^{i}·x+k_{y}^{i}·y)}+A^re^{i(k_{x}^{r}·x+k_{y}^{r}·y)}]=\hat{z} × A^te^{i(k_{x}^{t}·x+k_{y}^{t}·y)}, \nonumber \]

Since this equation must be satisfied for all points (x, y), it follows that

\[k_{x}^{i}=k_{x}^{r}=k_{x}^{t}, \nonumber \]

\[k_{y}^{i}=k_{y}^{r}=k_{y}^{t}, \nonumber \]

Hence, the tangential components of the wave vectors of the incident, reflected and transmitted waves are identical. In fact, if (\(\PageIndex{19}\)) would not hold, then by keeping y fixed, the exponential functions in (\(\PageIndex{18}\)) would not all have the same periodicity as functions of x and then (\(\PageIndex{18}\)) could never be satisfied for all x. The same argument with x kept fixed leads to the conclusion (\(\PageIndex{20}\)).

Without restricting the generality, we will from now on assume that the coordinate system is chosen such that

\[k_{y}^{i}=k_{y}^{r}=k_{y}^{t}=0. \nonumber \]

The plane through the incident wave vector and the normal to the interface is called the plane of incidence. Hence in the case of (\(\PageIndex{21}\)) the plane of incidence is the (x, z)-plane.

Since the length of the wave vectors ki and kr is k₀n_i, with k₀ the wave number in vacuum and n_i = (E_i/E₀)^1/2 the refractive index, and since the length of kt is k₀n_t , with n_t = (E_t/E₀)^1/2, it follows from (\(\PageIndex{19}\))

\[sin θ_{i} = \dfrac{k_{x}^{i}}{k_{0}n_{i}}=\dfrac{k_{x}^{r}}{k_{0}n_{r}}=sin θ_{r}, \nonumber \]

and

\[n_{i}sin θ_{i} = \dfrac{k_{x}^{i}}{k_{0}}=\dfrac{k_{x}^{t}}{k_{0}}=n_{t}sin θ_{t}, \nonumber \]

where the angles are as in Figure \(\PageIndex{2}\). Hence,

\[θ_{i} = θ_{r}, angle\space of\space reflection = angle\space of\space incidence, \nonumber \]

\[n_{i}sin θ_{i} =n_{t}sin θ_{t},Snell’s\space Law . \nonumber \]

Snell’s Law implies that when the angle of incidence θ_i increases, the angle of transmission increases as well. If the medium in z < 0 is air with refractive index n_i = 1 and the other medium is glass with refractive index n_t = 1.5, then the maximum angle of transmission occurs when θ_i = 90^o with

\[θ_{t,max} = arcsin(n_{i}/n_{t}) = 41.8^o. \nonumber \]

Figure \(\PageIndex{2}\): The incident, reflected, and transmitted wave vectors with the electric and magnetic vectors for s- and p-polarisation. For s-polarisation the electric field points out of the plane at the instant shown while for p-polarisation the magnetic field points out of the plane at the instant shown.

In case the light is incident from glass, i.e. n_i = 1.5 and n_t = 1.0, the angle of incidence θ_i cannot be larger than 41.8^o because otherwise there is no real solution for θ_t . It turns out that when θ_i > 41.8^o , the wave is totally reflected and there is no propagating transmitted wave in air. As explained in Section 1.9.5, this does however not mean that there is no field in z > 0. In fact there is a non-propagating so-called evanescent wave in z > 0. The angle θ_i,crit = 41.8^o is called the critical angle of total internal reflection. It exists only if a wave is incident from a medium with larger refractive index on a medium with lower refractive index (n_t < n_i). The critical angle is independent of the polarisation of the incident wave.

1.9.3 Fresnel Coefficients

Because of (\(\PageIndex{19}\)) and (\(\PageIndex{21}\)), we write k_x = kⁱ_x = k^r_x = k^t_x and therefore kⁱ_z = (k²₀E_i − k²_x)^1/2 = −k^r_z and k^t_z = (k²₀E_t − k²_x)^1/2 . Hence,

\[k^i = k_{x}\hat{x} + k^i_{z}\hat{z}, k^r = k_{x}\hat{x} − k^i_{z}\hat{z}, \nonumber \]

and

\[k^t =k_{x}\hat{x} − k^t_{z}\hat{z}, \nonumber \]

According to (1.6.11), for the incident, reflected and transmitted plane waves there must hold:

\[A^i · k^i = A^r · k^r = A^t · k^t = 0. \nonumber \]

We choose an orthonormal basis perpendicular to kⁱ with unit vectors:

\[\hat{s}= \hat{y} , \hat{p}^i=\dfrac{1}{|k^i|}(-k_{z}^i\hat{x}+k_{x}\hat{z}), \nonumber \]

where

\[|k^i|= (k^i · (k^i)^*)^{1/2}=(k_{x}^2 · |k_{z}^i|^2)^{1/2}, \nonumber \]

and where in writing the complex conjugate we anticipate the case the kⁱ_z is complex, which may happen for example when E_i is complex (a case that has been excluded so far but which later will be considered) or in the case of evanescent waves discussed in Section 1.9.5. Note that when kⁱ_z is real, |k_i| = (k²_x + (kⁱ_z)_²)^1/2 = k0ni . It is easy to see that the basis (\(\PageIndex{30}\)) is orthonormal in the space of two-dimensional complex vectors and that s · kⁱ = pⁱ · kⁱ = 0. The vector s is perpendicular to the plane of incidence, therefore the electric field component in this direction is polarised perpendicular to the plane of incidence and is called s-polarised ("Senkrecht" in German). The other basis vector pⁱ is (for real kⁱ ) parallel to the plane of incidence and when the electric component in this direction is called p-polarised. The complex vector Aⁱ can be expanded on this basis:

\[A^i = A^i_{s} \hat{y} + A^i_{p} \hat{p}^i. \nonumber \]

Since

\[k^i × \hat{y} = |k^i|\hat{p}^i, k^i × \hat{p}^i =-\dfrac{k^2_{0}E_{i}}{|k^i|}\hat{y}, \nonumber \]

it follows that the electric and magnetic field of the incident plane wave can be written as

\[E^i(r) =(A^i_{s} \hat{y} + A^i_{p} \hat{p}^i)e^{ik^i·r}, \nonumber \]

\[H^i(r) = (\dfrac{|k^i|}{ωµ_{0}}A^i_{s}\hat{p}^i-\dfrac{ωE_{0}E_{i}}{|k^i|}A^i_{p}\hat{y})e^{ik^i·r}. \nonumber \]

The reflected field is expanded on the basis y and p^r with

\[\hat{p}^r=-\dfrac{1}{|k^i|}(k^i_{z}\hat{x}+k_{x}\hat{z}). \nonumber \]

The sign in front of the unit vector p^r is chosen such that that its x-component is the same as that of pⁱ . Since

\[k^r × \hat{y} = -|k^i|\hat{p}^r, k^r × \hat{p}^r =\dfrac{k^2_{0}E_{i}}{|k^i|}\hat{y}, \nonumber \]

it follows that

\[E^r(r) =(A^r_{s} \hat{y} + A^r_{p} \hat{p}^r)e^{ik^r·r}, \nonumber \]

\[H^r(r) = (-\dfrac{|k^i|}{ωµ_{0}}A^r_{s}\hat{p}^r+\dfrac{ωE_{0}E_{i}}{|k^i|}A^r_{p}\hat{y})e^{ik^r·r}, \nonumber \]

where we used that k^r · k^r = k₀²n_i² and |k^r| = (k_x² + |k_z^r|²)^1/2 = (k_x² + |k_zⁱ|²)^1/2 = |kⁱ|. For the transmitted plane wave we use the basis y and p^t with

\[\hat{p}^t=\dfrac{1}{|k^t|}(-k^t_{z}\hat{x}+k_{x}\hat{z}), \nonumber \]

where p^t is chosen such that the x-component of p^t has the same sign as the x-component of pⁱ. Since

\[k^t × \hat{y} = |k^t|\hat{p}^t, k^t × \hat{p}^t =\dfrac{k^2_{0}E_{t}}{|k^t|}\hat{y}, \nonumber \]

we get

\[E^t(r) =(A^t_{s} \hat{y} + A^t_{p} \hat{p}^t)e^{ik^t·r}, \nonumber \]

\[H^t(r) = (\dfrac{|k^t|}{ωµ_{0}}A^t_{s}\hat{p}^t-\dfrac{ωE_{0}E_{i}}{|k^t|}A^t_{p}\hat{y})e^{ik^t·r}, \nonumber \]

We now consider an s-polarised incident plane wave, i.e. A_pⁱ= 0. We will show that all boundary conditions can be satisfied by A_p^r = A_p^t = 0 and by appropriately expressing A_s^r and A_s^t in terms of A_sⁱ . This implies that if the incident plane wave is s-polarised, the reflected and transmitted waves are s-polarised as well. For s-polarisation, the electric field has only a y-component and this component is tangential to the interface z = 0. This leads to the condition

\[A^i_{s}+A^r_{s}=A^t_{s}. \nonumber \]

The only tangential component of the magnetic field is the x-component and requiring it to be continuous for z = 0 leads to

\[-k^i_{z}A^i_{s}+k^i_{z}A^r_{s}=-k^t_{z}A^t_{s}. \nonumber \]

Solving (\(\PageIndex{44}\)), (\(\PageIndex{45}\)) for A_s^r and A_s^t gives the following formula for the reflection and transmission coefficients:

\[r_{s}=\dfrac{ A^r_{s} }{ A^i_{s} }=\dfrac{ k^i_{z} -k^t_{z} }{k^i_{z} +A^t_{z} }, \nonumber \]

\[t_{s}=\dfrac{ A^t_{s} }{ A^i_{s} }=\dfrac{ 2k^i_{z} }{k^i_{z} +A^t_{z} }. \nonumber \]

Only the magnetic field has a z-component and it easy to verify that H_zⁱ + H_z^r = H_z for z = 0.

By looking at the case of a p-polarised incident wave: A_sⁱ = 0, we see that the expression for the magnetic field in the p-polarised case become similar (except for the chosen signs) to that of the electric field for s-polarisation and conversely. Enforcing the continuity of the tangential components at z = 0 gives for p-polarisation:

\[r_{p}=\dfrac{ A^r_{p} }{ A^i_{p} }=-\dfrac{ \dfrac{k^i_{p}}{E_{i}} -\dfrac{k^t_{p}}{E_{t}}}{\dfrac{k^i_{p}}{E_{i}} +\dfrac{k^t_{p}}{E_{t}}} , \nonumber \]

\[t_{p}=\dfrac{ A^t_{p} }{ A^i_{p} }=\dfrac{ 2 \dfrac{k^i_{p}}{E_{i}} }{ \dfrac{k^i_{p}}{E_{i}} +\dfrac{k^t_{p}}{E_{t}} }. \nonumber \]

It is easy to verify that E_z is the only normal component and that e_i(E_zⁱ + E_z^r ) = e_tE_z^t for z = 0.

The reflection and transmission coefficients r_s, r_p, t_s and tp are called Fresnel coefficients. As follows from the derivation, there is no cross talk between s- and p-polarised plane waves incident on a planar interface. A generally polarised incident plane wave can always be written as a linear combination of s- and a p-polarised incident plane waves. Because in general r_s ≠ r_p and t_s ≠ t_p , it follows that the reflected and transmitted fields are also linear combinations of s- and p-polarised fields, but with different coefficients (weights) of these two fundamental polarisation states than for the incident wave.

Remarks.

1. In the derivation of the Fresnel coefficients the continuity of the normal field components was not used and was automatically satisfied. The reason is that the electromagnetic fields of the plane waves where chosen to be perpendicular to the wave vectors. This implies that the divergence of Eε and of H vanishes which in turns implies that the normal components are automatically continuous across the the interface.

2. When kiz and ktz are both real, we have |kⁱ| = k₀n_i and |k^t| = k₀n_t and the Fresnel coefficients can be expressed in the angles θ_i, θ_r and θ_t and the refractive indices n_i = E_i^1/2/E₀ and n_t = (E_t/E₀)^1/2. Because k_zⁱ = k₀n_i cos θ_i and k_z^t = k₀n_t cos θ_t , we find

\[r_{s}=\dfrac{n_{i}cosθ_{i}-n_{t}cosθ_{t}}{n_{i}cosθ_{i}+n_{t}cosθ_{t}}=-\dfrac{sin(θ_{i}-θ_{t})}{sin(θ_{i}+θ_{t})}, \nonumber \]

\[t_{s}=\dfrac{2n_{i}cosθ_{i}}{n_{i}cosθ_{i}+n_{t}cosθ_{t}}=\dfrac{2cosθ_{i}sinθ_{t}}{sin(θ_{i}+θ_{t})}, \nonumber \]

and

\[r_{p}=-\dfrac{ \dfrac{cosθ_{i}}{n_{i}}- \dfrac{cosθ_{t}}{n_{t}}}{ \dfrac{cosθ_{i}}{n_{i}}- \dfrac{cosθ_{t}}{n_{t}} }=-\dfrac{tan(θ_{i}-θ_{t})}{tan(θ_{i}+θ_{t})}, \nonumber \]

\[t_{p}=\dfrac{\dfrac{2cosθ_{i}}{n_{i}}}{ \dfrac{cosθ_{i}}{n_{i}}+ \dfrac{cosθ_{t}}{n_{t}} }=-\dfrac{ 2cosθ_{i}sinθ_{t} }{tan(θ_{i}+θ_{t})}. \nonumber \]

To obtain the expressions at the far right in (\(\PageIndex{50}\)), (\(\PageIndex{51}\)), (\(\PageIndex{52}\)) and (\(\PageIndex{53}\)) Snell’s Law has been used.

3. The advantage of the expressions (\(\PageIndex{46}\)), (\(\PageIndex{47}\)), (\(\PageIndex{48}\)), (\(\PageIndex{49}\)) in terms of the wave vector components kiz and ktz is, that they also apply when k_zⁱ and/or k_z^t are complex. This happens for example when there is absorption in z < 0 or in z > 0 or both, or when E_i > E_t and the incident angle is above the critical angle, due to which k_z^t is purely imaginary (see Section 1.9.5).

Figure \(\PageIndex{3}\): Reflection and transmission coefficients as function of the angle of incidence of s- and p-polarised waves incident from air to glass. The Brewster angle θ_B is indicated.

1.9.4 Properties of the Fresnel Coefficients

For normal incidence: θ_i = 0, Snell’s Law implies: θ_t = 0. Hence, (\(\PageIndex{50}\)), (\(\PageIndex{52}\)) give:

\[r_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=\dfrac{n_{i}-n_{t}}{n_{i}+n_{t}}, \nonumber \]

Is is seen that for normal incidence r_p = r_s, as expected. Note however that if we would not have defined p^_r such that its tangential component is the same as that of pⁱ , the two reflection coefficients would have the opposite sign for normal incidence (as is the case in some books). If the incident medium is air and the other medium is glass (n_i = 1.0, n_t = 1.5), we get

\[r_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=-0.2, \nonumber \]

and since the flow of energy is proportional to the square of the field, it follows that 4% of normal incident light is reflected by the glass. Hence a lens of glass without anti-reflection coating reflects approximately 4% of the light at normal incidence. The transmission coefficient for normal incidence is:

\[t_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=\dfrac{2n_{i}}{n_{i}+n_{t}}, \nonumber \]

which for air-glass becomes 0.8.

Remark. Energy conservation requires that the normal component < Sz > of the time-averaged energy flux through the interface is continuous. By using the formula for the time-averaged Poynting vector of a plane wave (1.8.8), it can be verified that the Fresnel coefficients are such that the energy flux is indeed continuous.

It follows from Snell’s Law (\(\PageIndex{25}\)) that sin θ_t = (n_i/n_t) sin θ_i . Hence θ_t monotonically increases with θ_i and therefore there exists some θ_i such that

\[θ_{i}+θ_{t}=90^o. \nonumber \]

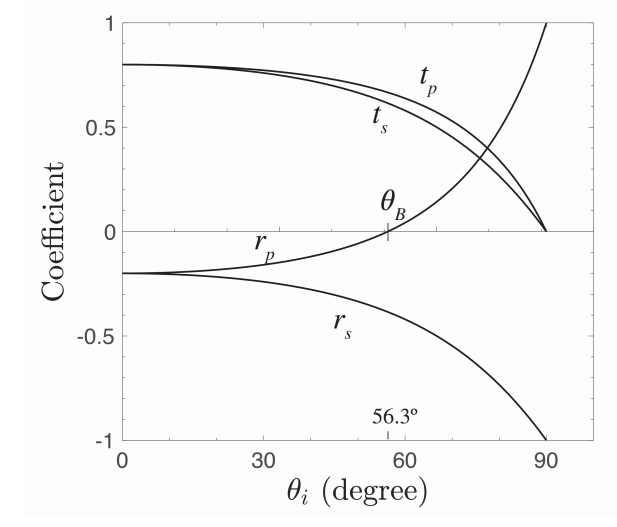
For this particular angle of incidence, the denominator of (\(\PageIndex{52}\)) is infinite and hence r_p = 0, i.e. the p-polarised wave is not reflected at all. This angle of incidence is called the Brewster angle θ_B . It is easy to see from (\(\PageIndex{50}\)) that the reflection is never zero for s-polarisation.

If unpolarised light is incident at the Brewster angle, the reflected light will be purely s-polarised.

Since at the Brewster angle s-polarised light is only partially reflected and the rest is transmitted, the transmitted light at the Brewster angle is a mixture of s- and p-polarisation. We have θ_t = 90^o − θ_i , hence sin θ_t = cos θ_i and by Snell’s Law (writing θ_i = θ_B):

\[tan(θ_{B})=\dfrac{n_{t}}{n_{i}}. \nonumber \]

We see that there is always a solution, independent of whether the wave is incident from the material with the smallest or largest refractive index. For the air-glass interface we have θ_B = 56.3^o and θ_t = 33.7^o . By (\(\PageIndex{50}\)):

\[r_{s}(θ_{B}=56.3^o)=-0.38 \nonumber \]

so that (0.38)²/2 = 0.07, or 7 % of the unpolarised light is reflected as purely s-polarised light at the air glass interface. For a wave incident from glass, θ_B = 33.7^o.

In Figure \(\PageIndex{3}\) the reflection and transmission coefficients of s- and p-polarised waves are shown as a function of the angle of incidence for the case of incidence from air to glass. There is no critical angle of total reflection in this case. The Brewster angle is indicated. It is seen that the reflection coefficients decrease from the values −0.2 for θ_i = 0^o to -1 for θ_i = 90^o . The transmission coefficients monotonically decrease to 0 at θ_i = 90^o.

Figure \(\PageIndex{3}\) shows the Fresnel coefficients when the wave is incident from glass to air. The critical angle is θ_i,crit = 41.8^o as derived earlier. At the angle of total internal reflection the absolute values of the reflection coefficients are identical to 1. There is again an angle where the reflection of p-polarised light is zero θ_B = 33.7^o.

Depending on the refractive indices and the angle of incidence, the reflection coefficients can be negative. The reflected electric field then has an additional π phase shift compared to the incident wave. In contrast, (provided that the materials are lossless), the transmitted field is always in phase with the incident field, i.e. the transmission coefficients are always positive.

1.9.5 Total Internal Reflection and Evanescent Waves

We return to the case of a wave incident from glass to air, i.e. n_i = 1.5 and n_t = 1. As has been explained, there is then a critical angle, given by sinθ_i,crit=n_t/n_i.

This is equivalent to

\[k_{x}^t=k_{0}n_{i}sinθ_{i,crit}=k_{0}n_{t} \nonumber \]

The wave vector k^t = k_x^tx + k_z^tz in z > 0 satisfies:

\[(k_{x}^t)^2+(k_{z}^t)^2=k_{0}^2n_{t}^2. \nonumber \]

Because of (\(\PageIndex{60}\)), we have at the critical angle

\[k_{z}^t=0. \nonumber \]

For angles of incidence above the critical angle we have: k_x^t > k₀n_t and it follows from (\(\PageIndex{61}\)) that (k_z^t)² = k₀²n_t² − (k_x^t)² < 0, hence k_z^t is imaginary:

\[k_{z}^t=±(k_{0}^2n_{t}^2-(k_{x}^t)^2)^{1/2}=±i((k_{x}^t)^2-k_{0}^2)^{1/2}, \nonumber \]

where the last square root is a positive real number. It can be shown that above the critical angle the reflection coefficients are complex numbers with modulus 1: |r_s| = |r_p| = 1. This implies that the reflected intensity is identical to the incident intensity, while at the same time the transmission coefficients are not zero! For example, for s-polarisation we have according to (\(\PageIndex{46}\)), (\(\PageIndex{47}\)):

\[t_{s}=1+r_{s}≠0, \nonumber \]

because r_s ≠ −1 (although |r_s| = 1). Therefore there is an electric field in z > 0, given by

\[E(x,z)e^{-iωt}=t_{s}e^{ik_{x}^tx+ik_{z}^tz-iωt}\hat{y}=t_{s}e^{i(k_{x}^tx-ωt)}e^{-z((k_{x}^t)^2-k_{0}^2n_{t}^2)^{1/2}}\hat{y},z>0, \nonumber \]

where we have chosen the + sign in (\(\PageIndex{63}\)) to prevent the field from blowing up for z → ∞. Since k_x^t is real, the wave propagates in the x-direction. In the z-direction, however, the wave is not propagating. Its amplitude decreases exponentially as a function of distance z to the interface and therefore the wave is confined to a thin layer adjacent to the interface. Such a wave is called an evanescent wave. One can compute the Poynting vector of the evanescent wave and find that this vector is parallel to the interface. Hence, the flow of energy of an evanescent wave propagates parallel to the interface namely in the direction in which k^t_x is positive

Hence no energy is transported away from the interface into the air region. We shall return to evanescent waves in the chapter on diffraction theory.

External sources in recommended order

1. Youtube video - 8.03 - Lect 18 - Index of Refraction, Reflection, Fresnel Equations, Brewster Angle - Lecture by Walter Lewin

2. MIT OCW - Reflection at The Air-glass Boundary: demonstration of reflection of polarised light and the Brewster angle.