3.8: The Compound Microscope

A magnifier alone can provide very high magnification only at the cost of intolerable aberrations. The compound microscope is a magnifier of close objects with a high angular magnification, generally more than $30 \times$. It was invented by Zacharias Janssen in Middelburg in 1590 (this claim is disputed). The first element of the compound microscope is an objective (in Figure $\PageIndex{1}$ a simple positive lens) which makes a real, inverted and magnified image of the object in the front focal plane of an eyepiece (where there is also the field stop). The eyepiece will make a virtual image at infinity, as explained above. The magnifying power of the entire system is the product of the transverse linear magnification of the objective $M_{T}$ and the angular magnification of the eyepiece $M_{A e}$ : $$\mathrm{MP}=M_{T} M_{A e} . \nonumber$$

Figure $\PageIndex{1}$: Simple compound microscope. The objective forms a real image of a nearby object. The eyepiece enlarges this intermediate image. The final image can be bigger than the barrel of the device, since it is virtual.

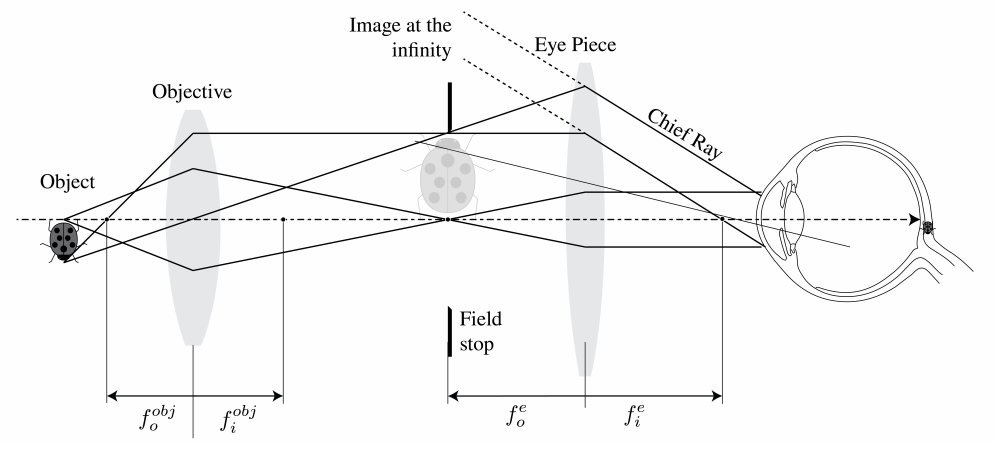
According to (2.5.51): $M_{T}=-x_{i} / f_{i}^{o b j}$, where $x_{i}$ is the distance of the image made by the objective to its back focal plane with focal distance $f_{i}^{\text {obj }}$. We have $x_{i}=L$ which is the tube length, i.e. the distance between the second focal point of the objective and the first focal point of the eyepiece. The tube length is standardised at $16 \mathrm{~cm}$. Furthermore, according to (3.5.5), the angular magnification is for a virtual image at infinity $M_{A e}=d_{o} / f_{i}^{e}$. Hence, we obtain: $$\mathrm{MP}=\frac{-x_{i}}{f_{i}^{o b j}} \frac{d_{o}}{f_{i}^{e}}=\frac{-16}{f_{0}} \frac{25}{f_{e}}, \nonumber$$ with the standard near-point $d_{o}=25 \mathrm{~cm}$. As an example, an Amici objective gives $40 \times$ and combined with a $10 \times$ eye piece one gets $M P=400$.

The Numerical aperture of a microscope is a measure of the capability to gather light from the object. It is defined by: $$\mathrm{NA}=n_{i m} \sin \theta_{\max } \nonumber$$ with $n_{\text {im }}$ the refractive index of the immersing medium, usually air, but it could be water or oil, and $\theta_{\max }$, the half-angle of the maximum cone of light accepted by the lens. The numerical aperture is the second number etched in the barrel of the objective. It ranges from $0.07$ (lowpower objectives) to $1.4$ for high-power objectives. Note that it depends on the object distance. In Chapter 7 it will be explained that NA is for the a given object distance proportional to the resolving power, which is the minimum transverse distance between two object points that can be resolved in the image.