7.2: Optical Resonator
- Page ID
- 57634
We now explain the working of lasers. A laser consists of
- an optical resonator;
- an amplifying medium.
In this section we consider the resonator. Its function is to obtain a high light energy density and to gain control over the emission wavelengths.
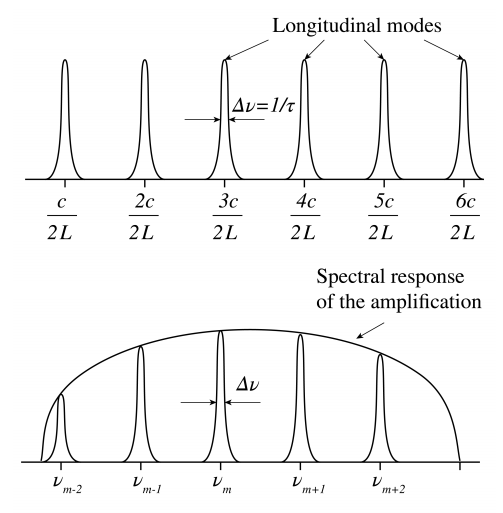
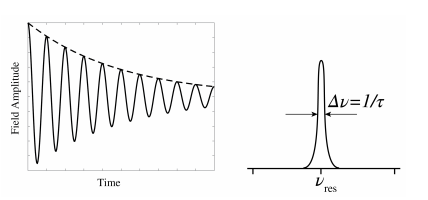
A resonator, whether it is mechanical like a pendulum, a spring or a string, or electrical like an LRC circuit, has one or multiple resonance frequencies \(\nu_{\text {res.}}\). Every resonator has losses due to which the oscillation gradually dies out when no energy is supplied. The losses cause an exponential decrease of the amplitude of the oscillation, as shown in Figure \(\PageIndex{1}\). The oscillation is therefore not purely monochromatic but has a finite bandwidth of order \(\Delta \nu \approx 1 / \tau\) as shown in Figure \(\PageIndex{1}\), where \(\tau\) is the time at which the amplitude of the oscillation has reduced to half the initial value.
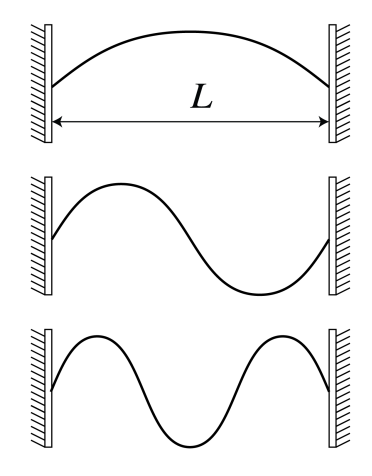
The optical resonator is a region filled with some material with refractive index \(n\) bounded by two aligned, highly reflective mirrors at a distance \(L\). The resonator is called a Fabry-Perot cavity. Let the \(z\)-axis be chosen along the axis of the cavity as shown in Fig.\(\PageIndex{2}\), and assume that the transverse directions are so large that the light can be considered a plane wave bouncing back and forth along the \(z\)-axis between the two mirrors. Let \(\omega\) be the frequency and \(k_{0}=\omega / c\) the wave number in vacuum. The plane wave that propagates in the positive \(z\)-direction is given by: \[E(z)=A e^{i k_{0} n z}. \nonumber \]
For very good mirrors, the amplitude remains unchanged upon reflections, while the phase typically changes by \(\pi\). Hence, after one round trip (i.e. two reflections) the field (\(\PageIndex{1}\)) is (the possible phase changes at the mirrors add up to \(2 \pi\) and hence have no effect): \[E(z)=A e^{2 i k_{0} n L} e^{i k_{0} n z} . \nonumber \] A high field builds up when this wave constructively interferes with (\(\PageIndex{1}\)), i.e. when \[k_{0}=\frac{2 \pi m}{2 n L}, \quad \text { or } \quad \nu=\frac{k c}{2 \pi}=m \frac{c}{2 n L}, \nonumber \] for \(m=1,2, \ldots\). Hence, provided dispersion of the medium can be neglected ( \(n\) is independent of the frequency), the resonance frequencies are separated by \[\Delta \nu_{f}=c /(2 n L), \nonumber \] which is the so-called free spectral range. For a gas laser that is \(1 \mathrm{~m}\) long, the free spectral range is approximately \(150 \mathrm{MHz}\).
Suppose that the cavity is \(100 \mathrm{~cm}\) long and is filled with a material with refractive index \(n=1\). Light with visible wavelength of \(\lambda=500 \mathrm{~nm}\) corresponds to mode number \(m=2 L / \lambda=4 \times 10^{6}\) and the free spectral range is \(\Delta \nu_{f}=c /(2 L)=150 \mathrm{MHz}\).
The multiple reflections of the laser light inside the resonator make the optical path length very large. For an observer, the atomic sources seem to be at a very large distance and the light that is exiting the cavity resembles a plane wave. The divergence of the beam is therefore not limited by the size of the source, but by diffraction due to the aperture of the exit mirror.
Because of losses caused by the mirrors (which never reflect perfectly) and by the absorption and scattering of the light, the resonances have a certain frequency width \(\Delta \nu\). When a resonator is used as a laser, one of the mirrors is given a small transmission to couple the laser light out. This also contributes to the loss of the resonator. To compensate for all losses, the cavity must contain an amplifying medium. Due to the amplification, the resonance line widths inside the bandwidth of the amplifier are reduced to very sharp lines as shown in Figure \(\PageIndex{3}\).
