1.2: Reflection at a Plane Surface
( \newcommand{\kernel}{\mathrm{null}\,}\)
The law of reflection of light is merely that the angle of reflection r is equal to the angle of incidence i. There is really very little that can be said about this, but I’ll try and say what little need be said.
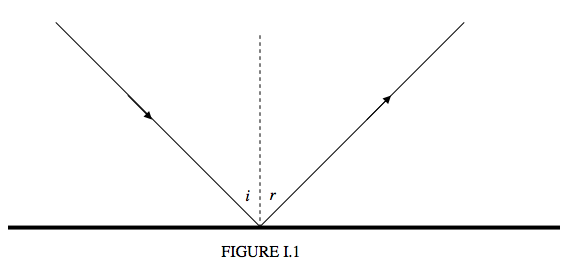
- It is customary to measure the angles of incidence and reflection from the normal to the reflecting surface rather than from the surface itself.
- Some curmudgeonly professors may ask for the lawS of reflection, and will give you only half marks if you neglect to add that the incident ray, the reflected ray and the normal are coplanar.
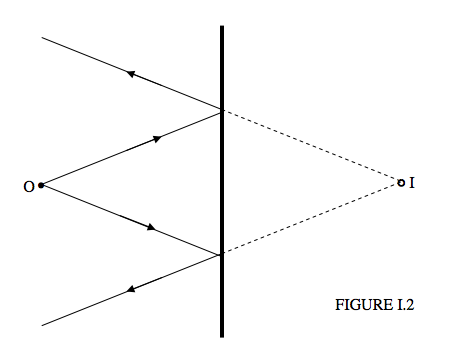
- A plane mirror forms a virtual image of a real object:
or a real image of a virtual object:
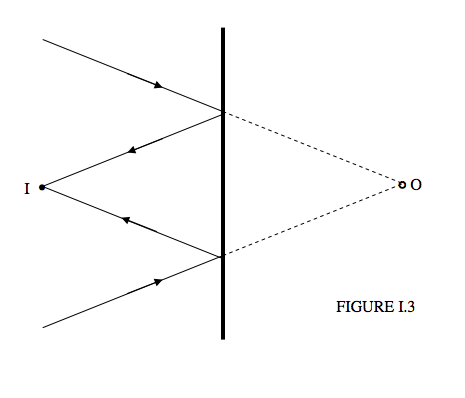
- It is usually said that the image is as far behind the mirror as the object is in front of it. In the case of a virtual object (i.e. light converging on the mirror, presumably from some large lens somewhere to the left) you’d have to say that the image is as far in front of the mirror as the object is behind it!
- If the mirror were to move at speed v away from a real object, the virtual image would move at speed 2v. I’ll leave you to think about what happens in the case of a virtual object.
- If the mirror were to rotate through an angle θ (or were to rotate at an angular speed ω), the reflected ray would rotate through an angle 2θ (or at an angular speed 2ω).
- Only smooth, shiny surfaces reflect light as described above. Most surfaces, such as paper, have minute irregularities on them, which results in light being scattered in many directions. Various equations have been proposed to describe this sort of scattering. If the reflecting surface looks equally bright when viewed from all directions, the surface is said to be a perfectly diffusing Lambert’s law surface. Reflection according to the r=i law of reflection, with the incident ray, the reflected ray and the normal being coplanar, is called specular reflection (Latin: speculum, a mirror). Most surfaces are intermediate between specular reflectors and perfectly diffusing surfaces. This chapter deals exclusively with specular reflection.
- The image in a mirror is reversed from left to right, and from back to front, but is not reversed up and down. Discuss.
- If you haven’t read Through the Looking-glass and What Alice Found There, you are missing something.
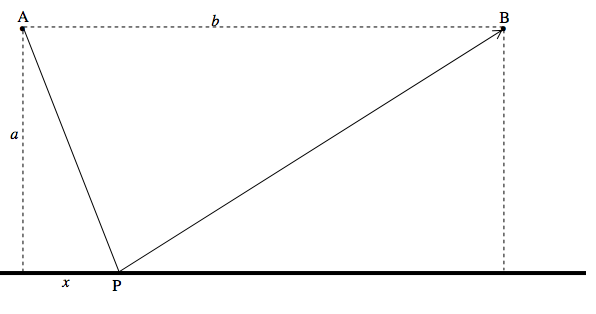
Light goes from A to B via reflection from a point P in a mirror.
The distance s traveled is given by
s=√a2+x2+√a2+(b−x)2
Here is the distance traveled as a function of the position of the point P:
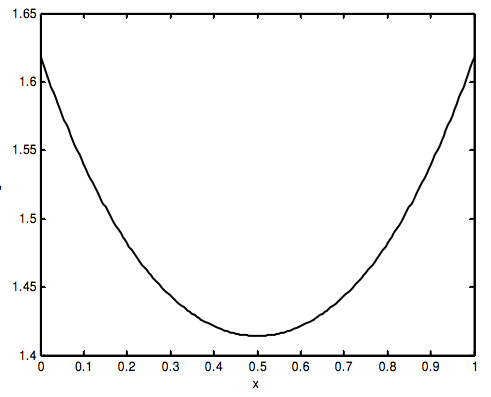
The path that the light actually takes is the path such that the distance traveled is a minimum, which is such that P is horizontally halfway between A and B. You can see this from the graph, or by differentiating the above expression for s. This means that the angle of reflection is equal to the angle of incidence. You may regard this observation as a slightly interesting trivium, or as a fundamental principle of the deepest significance. Whichever you choose, you will come across lots of other examples of nature operating with Least Action. And you won’t have to wait long. There’s another one in the next section.


