8.2: Strange Particles
( \newcommand{\kernel}{\mathrm{null}\,}\)
In 1947 the British physicists Rochester and Butler (from across the street) observed new particles in cosmic ray events. (Cosmic rays where the tool before accelerators existed – they are still used due to the unbelievably violent processes taking place in the cosmos. We just can’t produce particles like that in the lab. (Un)fortunately the number of highly energetic particles is very low, and we won’t see many events.) These particles came in two forms: a neutral one that decayed into a π+ and a π−, and a positively charge one that decayed into a μ+ (heavy electron) and a photon, as sketched in Figure 8.2.1.

The big surprise about these particles was how long they lived. There are many decay time scales, but typically the decay times due to strong interactions are very fast, of the order of a femto second (10−15 s). The decay time of the K mesons was about 10−10 s, much more typical of a weak decay. Many similar particles have since been found, both of mesonic and baryonic type (like pions or like nucleons). These are collectively know as strange particles. Actually, using accelerators it was found that strange particles are typically formed in pairs, e.g.,
π++p→Λ0⏟baryon+K0⏟meson
This mechanism was called associated production, and is highly suggestive of an additive conserved quantity, such as charge, called strangeness. If we assume that the Λ0 has strangeness −1, and the K0 +1, this balances
π++p→Λ0+K00+0=−1+1
The weak decay
Λ0→π−+p−1≠0+0,
does not conserve strangeness (but it conserves baryon number). This process is indeed found to take much longer, about 10−10 s.
Actually it is found (by analysing many resonance particles) that we can accommodate this quantity in our definition of isospin,
Q=e(I3+B+S2)
Clearly for S=−1 and B=1 we get a particle with I3=0. This allows us to identify the Λ0 as an I=0,I3=0 particle, which agrees with the fact that there are no particles of different charge and a similar mass and strong interaction properties.
The kaons come in three charge states K±, K0 with masses mK±=494MeV, mK0=498MeV. In similarity with pions, which form an I=1 multiplet, we would like to assume a I=1 multiplet of K’s as well. This is problematic since we have to assume S=1 for all these particles: we cannot satisfy
Q=e(I3+12)
for isospin 1 particles. The other possibility I=3/2 doesn’t fit with only three particles. Further analysis shows that the the K+ is the antiparticle of K−, but K0 is not its own antiparticle (which is true for the pions. So we need four particles, and the assignments are S=1,I=1/2 for K0 and K−, S=−1,I=1/2 for K+ and ˉK0. Actually, we now realize that we can summarize all the information about K’s and π’s in one multiplet, suggestive of a (pretty badly broken!) symmetry.

However, it is hard to find a sensible symmetry that gives a 7-dimensional multiplet. It was argued by Gell-Mann and Ne’eman in 1961 that a natural extension of isospin symmetry would be an SU(3) symmetry. We have argued before that one of the simplest representations of SU(3) is 8 dimensional symmetry. A mathematical analysis shows that what is missing is a particle with I=I3=S=0. Such a particle is known, and is called the η0. The breaking of the symmetry can be seen from the following mass table:
mπ±=139MeVmπ0=134MeVmK±=494MeVm(−)K0=498MeVmη0=549MeV
The resulting multiplet is often represented like in Figure 8.2.3.

In order to have the scheme make sense we need to show its predictive power. This was done by studying the nucleons and their excited states. Since nucleons have baryon number one, they are labelled with the “hyper-charge” Y,
Y=(B+S),
rather than S. The nucleons form an octet with the single-strangeness particles Λ and σ and the doubly-strange cascade particle Ξ (Figure 8.2.4).

The masses are
Mn=938MeVMp=939MeVMΛ0=1115MeVMΣ+=1189MeVMΣ0=1193MeVMΣ−=1197MeVMΞ0=1315MeVMΞ−=1321MeV
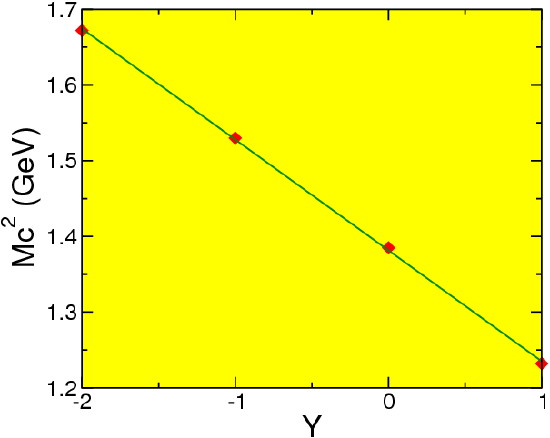
All these particles were known before the idea of this symmetry. The first confirmation came when studying the excited states of the nucleon. Nine states were easily incorporated in a decuplet, and the tenth state (the Ω−, with strangeness -3) was predicted. It was found soon afterwards at the predicted value of the mass.

The masses are
MΔ=1232MeVMΣ∗=1385MeVMΞ∗=1530MeVMΩ=1672MeV
(Notice almost that we can fit these masses as a linear function in Y, as can be seen in Figure 8.2.6. This was of great help in finding the Ω.)