12: A quantum paradox and the experiments
( \newcommand{\kernel}{\mathrm{null}\,}\)
Quantum mechanics makes probabilistic predictions about the possible outcomes of an experiment with microscopic objects, particles. This is a statistical statement concerning many particles. One can assume that there exists a deeper non-statistical, i.e. deterministic law for single particles predicting what should happen with that specific particle.
Is there any deeper theory or law determining the experimental result with certainty? There must be such a theory according to Einstein, implying that quantum mechanics cannot be a complete theory. On the other hand, according to Bohr – who was another founder of quantum theory – there is no place for a deeper theory, we cannot predict anything more about a single particle, but probabilities.
Chapter 1. Polarization of plane light waves in classical optics.
The EPR-paradox, Bohm’s version
In this last section we consider certain principal questions of quantum mechanics that are connected with the very essence of the subject, i.e. with the nature of the probabilities appearing in the theory. In classical physics a measurement makes a record of the value of a physical quantity of a particle, a body, or a system which is assumed to be a property of the particle that existed prior to the measurement, and independently whether we measure it or not. In contrast to this, in quantum physics – a set of particles can be prepared to have exactly the same property from a certain point of view, still they can show up quite different measurement results, from the point of view of another property.
The simplest example is connected with light polarization, or stated in quantum language: photon polarization. According to quantum mechanics if a plane transversal wave is polarized, and its plane of polarization makes an angle θ with another polarization direction, then the photons in the beam are polarized also in that latter direction with a probability amplitude cosθ. This means, for instance, that if the polarization makes an angle θ with the horizontal direction and therefore an angle π/2−θ with the vertical direction, then the corresponding probability amplitudes are cosθ and cos(π/2−θ)=sinθ, respectively. According to the fundamental role of quantum physics the probabilities are in turn the (absolute value) squares of the amplitudes. So the probability of finding a single photon of the original beam to be polarized horizontally is cos2θ while the probability of being vertically polarized is sin2θ. This law is easily verified already with a classical plane wave field of intensity I0 which is polarized so that it makes an angle θ with the horizontal direction. The beam is directed to a calcite crystal which separates it into two beams so that one of them is polarized horizontally the other one vertically – these are the eigendirections of the calcite – and the two beams are distinct, so that they can be checked individually. Then the intensity of the horizontally polarized beam after the calcite will be I0cos2θ, while that of the vertically polarized beam will be I0sin2θ. As the intensity is proportional to the number of photons, this is a proof of the probability law. Present day technique allows also to check the probabilities themselves, because photons can also be detected one by one by sensitive detectors.
It will be important that we can set the calcite so that its eigendirections are not horizontal and vertical, which we shall call setting A later on, but also in a way, say B or C, so that the two eigendirections are different from those of the setting A. Let us note, however, that the two eigendirections are always orthogonal to each other.
The following question arises: what determines the final polarization direction of the photon. According to quantum mechanics the photon becomes vertical, or horizontal during the interacion with the measurement apparatus. This is not encoded in the incoming particle, therefore it is principally impossible to answer the question with certainty, most we can say are the probabilities of the two different possible outcomes. Stated in another way, the measurement does not establish a previously existing property of the photon, rather it is the measurement itself that creates the property with the appropriate probability.
This answer, however, does not satisfy everybody, because one can imagine a different answer, as well, namely assuming that for each photon both properties did exist before the measurement, i.e. it was polarized in say 45∘ and at the same time it had the property of being horizontally polarized, if we obtained the latter result during the measurement. It is another question that quantum mechanics does not give account of both properties simultaneously, as it cannot give with unit probability – i.e. with complete certainty – the direction of polarization of a single photon for two non-parallel or nonorthogonal directions. This would mean then that there exists a kind of a theory, deeper than quantum mechanics, according to which these properties are present simultaneously and exactly in the measured object. From the point of view of quantum theory the parameter that would give the result with certainty is not present, so it is a hidden parameter as it is called in these theories.
As quantum mechanics does not give account of these parameters, it cannot be a complete description of physical reality. This was the point of view of A. Einstein, and this was exposed in the most perplexing way in the famous paper by A. Einstein, B. Podolsky and N. Rosen in 1935: ‟Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” In the end of the work they came to the conclusion that quantum mechanics is not complete, but they add that such a theory shall appear in the future.
In the beginning the authors of the EPR paper try to give an exact definition what they consider a complete theory:
“A theory is complete if every element of physical reality has its counterpart in the physical theory.”
But what is an element of physical reality? They give the following answer:
“If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding lo this physical quantity.”
Einstein, Podolsky and Rosen (EPR) present the description and the analysis of an imagined experiment, (so called Gedankenexperiment) performed on a pair of quantum particles, which according to the authors shows that quantum mechanics is not a complete theory in the sense they require it. In their example they consider the measurement of the positions and the momenta of a pair of particles, which emerge in a disintegration process. Instead of that it is simpler to consider another variant of the experiment, when it is done with a pair of two-state systems, as there are only two possible results in a single measurement apparatus, instead of the infinitely many possible outcomes when measuring position or/and momenta. Such a variant of the EPR paradox was proposed by David Bohm in 1957 with pairs of spin 1/2 particles, or what we shall analyze, with photons having two orthogonal polarization eigenstates.
The essential features of the experiment, performed many times since Bohm’s proposal, are the following. A special source generates pairs of photons, such that the members of the pair propagate in different spatial directions, say, one to the left, the other to the right. The polarization properties of the members are measured independently. One places two polarization measurement devices perpendicularly to the propagation of the beams. These are e.g. calcite crystals in the paths of the two photons which pass through them, and measure the polarization properties of the photons. The devices can be set making different angles with the horizontal direction. The possible settings of the devices will be denoted by different capital letters A,B,C and the two corresponding eigenstates of the devices by A+ and A−; B+ and B−; and C+ and C− respectively. With an appropriate photon source one can achieve that there is a strict anticorrelation in the measurement between the members of a pair, which means the following. Assume that the devices are set identically, on both sides of the source. Then both photons pass through the same type of device, say horizontal-vertical, to be denoted by A. One observes then that if one of the photons is polarized horizontally A− on the left, its pair turns always out to be vertically polarized A+, on the right, or vice versa. The same thing happens if both polarizers are set in any direction say B which is different from A, but identical for both photons. If B+ denotes 60∘ from the horizontal and B− means −30∘ from the horizontal, then if one of the photons comes is polarized in B+, its pair will be B−, or the other way round. Thus the polarization states of a given member are always orthogonal to each other. Such pairs of particles are called EPR pairs. This anticorrelation of the pair follows from the way one creates them, which will be detailed below.
An EPR state of a photon pair is:
ψ=1√2{(A+)1(A−)2−(A−)1(A+)2} (12.1)
where subscript labels the particle: 1 goes to left and 2 to the right. The first term in the state above says that photon 1 is polarized vertically, while photon 2 is polarized horizontally. The second term means all this the other way round. What is important, quantum mechanics allows the superposition of the two possibilities. We have already encountered a similar state when we considered the spin singlet state of the two electrons in the H2 molecule in Chapter 7.
Show that the state (12.1) above cannot be written as a product of two one-particle states.
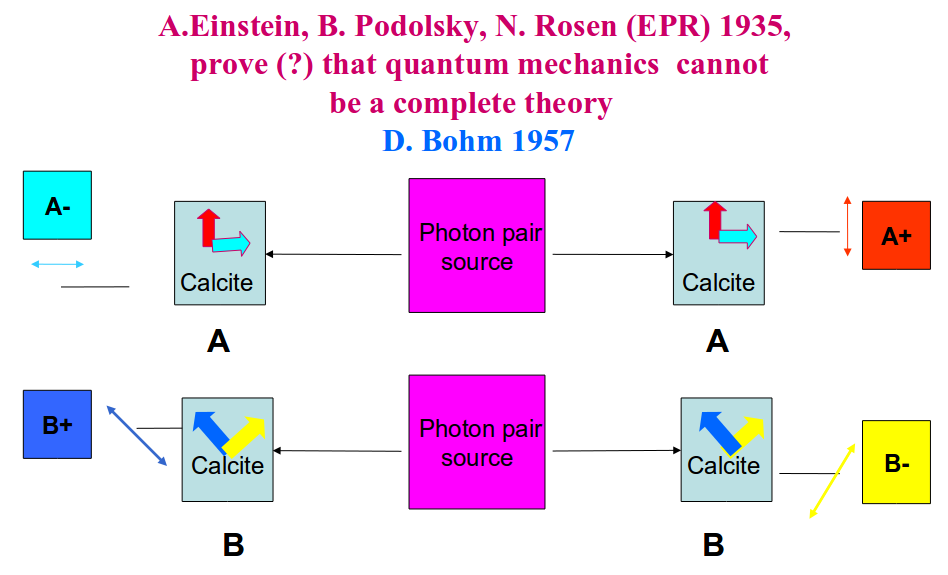
But then it is sufficient to measure only on one photon of the pair. We may think that we know the result for the other member, even without doing the measurement, because it will be always opposite to the one for its partner. Therefore without disturbing it, we can predict its value, thus it is the element of reality according to EPR. One has to add here, that it is impossible that we measure a value A+ on the left because we measured A− on the right. The propagation of this information needs time, but the two events can have a space-like separation (in the sense of relativity theory), which means that only a signal faster than light could influence the result of the measurement on the other side, depending on the result of one of the sides. This is the locality principle emphasized so much by Einstein’s theory of relativity. To conclude: the polarization property of the unmeasured photon is the element of reality, and a complete theory must assign a well defined value to it in the sense defined by EPR.
But there is even more than that: in the case of the EPR pair we can tell the state of a particle exactly even from the point of view of two incompatible devices, what is impossible in quantum mechanics, in principle. Let us put two different devices on the two sides.
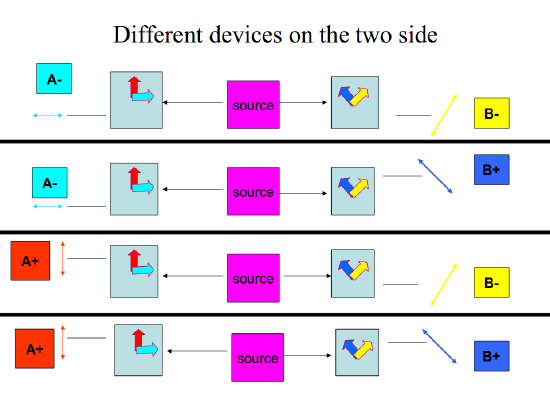
If we measure on the left side the property A (physical quantity), then we also know the state of its pair on the right from the point of view of A, due to the perfect anticorrelation. It will be perpendicular to the direction measured on the left. But at the same time on the right we may measure with another type of apparatus, that measures the property B. In this way we can state both properties of the given particle, one of them follows from the measured value on its mate on the left, the other one is measured actually. The same is true for its partner. This would mean that both properties are well defined in the case of a single particle, while according to QM this is impossible, if A and B have different eigendirections as seen in figure 12.2. In quantum mechanics only the probability amplitude and a corresponding probability is given if A and B make an angle different from 0∘ or 90∘. This reasoning led EPR to the conclusion that QM, which does not give account for two incompatible elements of physical reality, cannot be complete. In contrast to the statement by EPR, N. Bohr argued that the two particles are part of a single unseparable quantum system, according to the present wording they are in an entangled state, therefore a measurement on one of its parts immediately influences its other part, even if they are very far from each other let the two measurements two spacelike events in the sense of special relativity. But this statement contradicted to one of the most fundamental principles of physics, locality. Therefore Einstein could not accept Bohr’s arguments and the debate and the paradox remained unsolved for about 30 years.
Bell-inequalities with photons
In order to decide the question, John Bell proposed an explicit experimental arrangement in 1964. One has to measure not two but three different quantities (orthogonal polarizations) A, B, and C for the photon pairs, so that the three possible settings of the polarizers are chosen randomly and independently from each other. It turns out, that based on the experimentally measured number of pairs one can decide whether quantum mechanics, or the Einstein hypothesis is correct, the latter saying that the particles must have well defined polarizations in different directions simultaneously. The original idea of Bell will be presented here as it was discussed by Eugene Wigner.

Assume that the members of the pair had a well defined polarization before the measurement: + or − in each of the three directions A, B, and C. As the measurements show, in a single pair the polarization of the two particles are always orthogonal to each other, shown up explicitly if we use the same settings on both sides. The possible 8 types of the pairs are shown in table 12.1, and let us denote the measured number of a given type of pairs by Nk.
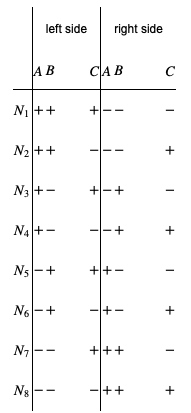
Table 12.1:
Let us consider now the pairs for which the particle going to left resulted in A+, while the one going to right came out as C+. These events will of course be present only if the device on the left was set to A while the one at right was set to C. The number of such pairs shall be denoted here by N(A+,C+), and according to the table above N(A+,C+)=N2+N4. Similarly the number of pairs for which we got A+A+ on the left and B+B+ on the right the result is N(A+,B+)=N3+N4. Finally the number of those where we had B+ on the left and C+ on the right was N(B+,C+)=N2+N6.
According to the simple inequality
N2+N4≤(N3+N4)+(N2+N6) (12.2)
valid because by definition all the numbers Ni are nonnegative integers, we get:
N(A+,C+)≤N(A+,B+)+N(B+,C+) (12.3)
It is important that the number of pairs N(A+,C+),N(A+,B+),N(B+,C+) can be measured, and the experimental result can be compared with the inequality obtained above. Before going on, however, we reformulate the inequality (12.3) into probabilities, in order to compare it with quantum mechanics, which give its results in terms of probabilities.
Let P(A+,C+) the probability, that by choosing randomly the directions we set on the left the device to A, and it measured a result A+, while the measurement on the right particle happened again by random choice in the direction C, and resulted in C+. Then
P(A+,C+)=N(A+,C+)∑8i=1Ni (12.4)
and similarly P(A+,B+)=N(A+,B+)∑8i=1Ni,P(B+,C+)=N(B+,C+)∑Bi=1Ni, if we made sufficiently many measurements. Accordingly the inequality (12.3) can be written as
P(A+,C+)≤P(A+,B+)+P(B+,C+) (12.5)
This is a Bell inequality, which – as we must remember – was derived by using the assumption that the pairs had well defined properties before the measurement was performed. There were no quantum mechanical arguments in obtaining it.
So let us look at what QM says about the probabilities occurring in (12.5) as shown in the figure below. In a real measurement one has identical crystals on both sides, and they are rotated randomly and independently of each other in three directions A, B and C. If on the left side we measure A+ for instance, then its pair should be in state A−. But we measure say C on it, and the result measured on the partner can be either C+ or C−. The probability amplitude of getting the result that this other particle is polarized in the direction êθ is cosθ, where θ is the angle with A−. The corresponding probability is thus cos2θ. Or we wish to express it with the angle made with A+, which is α=π/2−θ, then the probability is sin2α. Choosing randomly the possible three directions on both sides with equal probabilities 1/3, the probability of all the possible settings of the pair of the apparatuses equals to 1/9. The probability of obtaining say A+A+ on the left before we measured on the right is 1/2, then with a given setting of both crystals the probability is e.g. P(A+,C+)=118sin2(A+,C+), where (A+,C+) denotes here the angle between the directions A+ and C+.
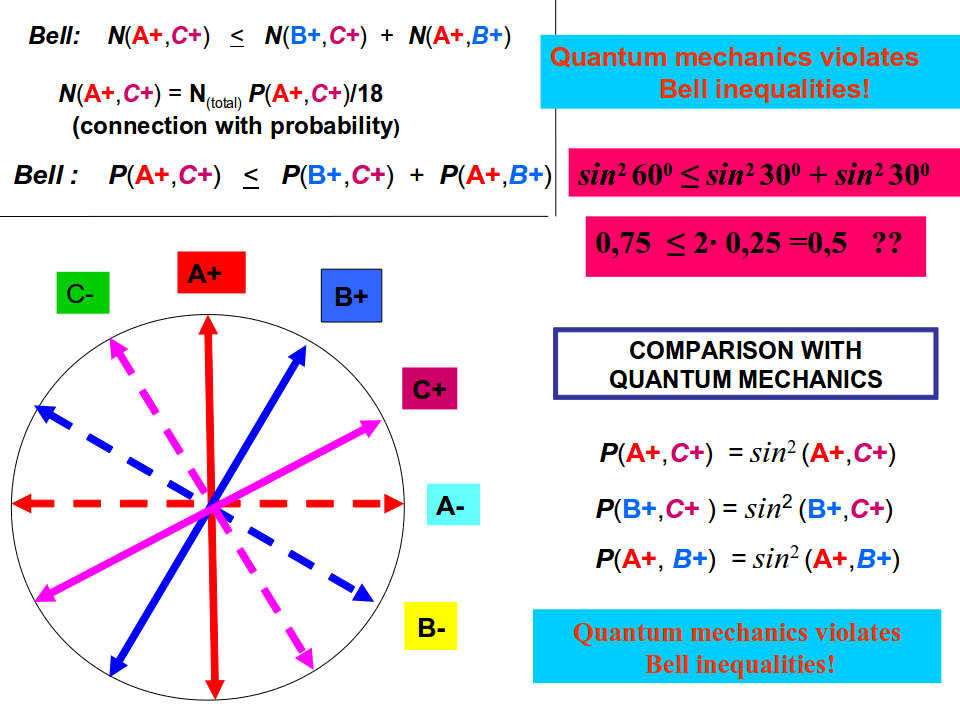
Let us choose specifically the directions shown in the figure, i.e. let the eigendirections of A, B and C be rotated consecutively by 30∘. In other words we choose (A+,B+)=(B+,C+)=30∘ and (A+,C+)=60∘. Then the quantum mechanical probabilities give the following result:
P(A+,C+)=118sin260∘,P(A+,B+)=118sin230∘,P(B+,C+)=118sin230∘ (12.6)
If we substitute these probabilities into (12.5) we observe that these results do not obey it, because that would require the fulfilment of sin260∘≤2sin230∘, i.e. the inequality
34≤12 (12.7)
which is obviously false.
This means that by choosing appropriate directions for the crystals the corresponding quantum mechanical probabilities violate the Bell inequality. This turns out to be then an experimental possibility to decide whether quantum mechanics or Bell inequalities are valid in the real physical world. According to the experiments measuring directly the numbers N(A+,C+) etc. it turned out that the Bell inequalities are not valid for appropriately chosen directions A, B, and C as above but the results are in agreement with the predictions of QM.
All this should mean that in the derivation of the Bell inequalities must be something that contradicts to what is in the real physical world. There are two possibilities of errors. One of them could have been that filling out the table 12.1 we assumed that a particle, and its partner possessed two, (actually three) different polarization properties already before the measurement, they did exist in them independently of the measurement that was performed on them later. The other possible error could be that there is a nonlocal communication between the two members of a pair, i.e. the measured state of one of the particles depends on the measurement on its distant partner. (However one can show, that information cannot be transmitted in this way with a speed faster than light, because information transfer would necessitate an additional classical communication channel, and the speed of the transfer is determined by the velocity of the classical signal. That means that locality is not violated in this sense). Both possibilities, as reasons of the discrepancy, contradict to traditional concepts about the natural world. In the first case it contradicts to the assumption that all the possible properties of a particle, including the incompatible properties, have a well defined value before and independently of the measurement. This assumption is usually called as realism. The second possibility contradicts to locality, in the sense that the measurement result influences instantaneously a distant, spatially separated other measurement.
Experiments and Bell inequalities
The first experiments about validity or violation of the Bell inequalities was performed by J. F. Clauser and co-workers in 1972. A later experiment by A. Aspect (1982) was the first, where the settings of the two crystals were made so that the separation of these two events was space-like, i.e. a light signal imagined to start from one of the crystals at the time of its measurement could not reach the other one before it measured the state of the other particle.
Here we show the setup of the experiment of A. Zeilinger (1995) where the pair of photons emerged from a nonlinear crystal.
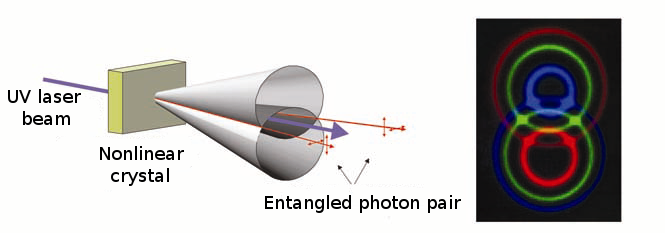
When the photons of an UV laser of wavelength 351 nm pass through the nonlinear crystal, a small part of them are split into two photons with smaller energy and thus with smaller frequency. This process is called parametric down conversion in nonlinear optics. The emerging two beams leave the crystal along the superficial of two cones, satisfying the energy and momentum conservation. Among the pairs some will share equally the original energy and momentum, their wavelength will be identically 702 nm (this is called the degenerate case). With an appropriate setting of the crystal one can achieve that the polarization of the members are always orthogonal to each other, as assumed for the EPR pair in the discussion above. In this latter case the angle at the apices of the two cones are identical and along their intersection – at the two green spots in the simulated figure on the right hand side of figure 12.5 – the photon pairs will have just the required property.
Downloading and running the exe file we can chose from three simulations. The first one demonstrates the violation of Bell inequality. The second one shows quantum teleportation, while the third is a realization of the BB84 quantum key distribution (QKD) protocol (not discussed here).
http://titan.physx.u-szeged.hu/~mmquantum/download.php?download_file=Qmdemo.exe
Experiments unanimously proved the validity of the quantum mechanical result and the violation of the Bell inequalities.