4.1: Bound States
( \newcommand{\kernel}{\mathrm{null}\,}\)
One of the simplest potentials to study the properties of is the so-called square well potential (Figure 4.1.1),
V(x)={0|x|>a−V0|x|<a
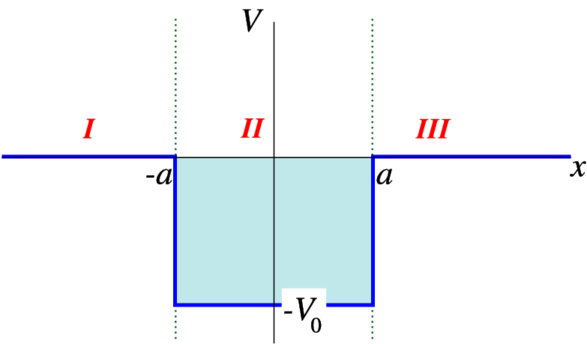
Figure 4.1.1: The square well potential
We define three areas, from left to right in Figure 4.1.1: I, II and III. In areas I and III we have the Schrödinger equation for a free particle
−ℏ22md2dx2ψ(x)=Eψ(x)
whereas in area II we have the equation
−ℏ22md2dx2ψ(x)=(E+V0)ψ(x)
In this class we shall quite often encounter the ordinary differential equations
d2dx2f(x)=−α2f(x)
which has as solution
f(x)=A1cos(αx)+B1sin(αx)=C1eiαx+D1e−iαx,
and
d2dx2g(x)=+α2g(x)
which has as solution
g(x)=A2cosh(αx)+B2sinh(αx)=C2eαx+D2e−αx.
Case 1: E> 0
Let us first look at E>0. In that case the equation in regions I and III can be written as
d2dx2ψ(x)=−2mℏ2Eψ(x)=−k2ψ(x),
where
k=√2mℏ2E
The solution to this equation is a sum of sines and cosines of kx, which cannot be normalized: Write
ψIII(x)=Acos(kx)+Bsin(kx)
where (A and B can be complex) and calculate the part of the norm originating in region III,
∫∞a|ψ(x)|2dx=∫∞a|A|2cos2kx+|B|2sin2kx+2ℜ(AB∗)sin(kx)cos(kx)dx=lim
We also find that the energy cannot be less than −V_0 , since we cannot construct a solution for that value of the energy. We thus restrict ourselves to − V_0< E< 0. We write
E = − \dfrac{ ℏ^2}{ k^2 2 m}
and
E + V_0 = \dfrac{ℏ^2κ^2}{2 m} . \label{4.11}
The solutions in the areas I and III are of the form (i=1,\,3)
ψ ( x ) = A_i e^{k x} + B_i e^{− k x}. \label{4.12}
In region II we have the oscillatory solution
ψ ( x ) = A_2 \cos ( κ x ) + B_2 \sin ( κ x ). \label{4.13}
Now we have to impose the conditions on the wave functions we have discussed before, continuity of ψ and its derivatives. Actually we also have to impose normalisability, which means that B_1= A_3= 0 (exponentially growing functions can not be normalized). As we shall see we only have solutions at certain energies. Continuity implies that
\begin{align} A_1 e^{ − k a} + B_1 e^{ k a} &= A_2 \cos ( κ a ) − B_2 \sin ( κ a ) \label{4.14A} \\[5pt] A_3 e^{k a} + B_3 e^{− k a} &= A_2 \cos ( κ a ) + B_2 \sin ( κ a ) \label{4.14B} \\[5pt] k A_1 e^{k a} − k B_1 e^{k a} &= κ A_2 \sin ( κ a ) + κ B_2 \cos ( κ a ) \label{4.14C} \\[5pt] k A_3 e^{ k a} − k B_3 e^{− k a} &= − κ A_2 \sin ( κ a ) + κ B_2 \cos ( κ a ) \label{4.14D} \end{align}
Tactical Approach
We wish to find a relation between k and κ (why?), removing as maby of the constants A and B. The trick is to first find an equation that only contains A_2 and B_2. To this end we take the ratio of Equations \ref{4.14A} and \ref{4.14C} and then the ratio of Equations \ref{4.14B} and \ref{4.14D}:
\begin{align} k &= \dfrac{κ [ A_2 \sin ( κ a ) + B_2 \cos ( κ a ) ]}{ A_2 \cos ( κ a ) − B_2 \sin ( κ a )} \label{4.15A} \\[5pt] k &= \dfrac{κ [ A_2 \sin ( κ a ) − B_2 \cos ( κ a ) ]}{ A_2 \cos ( κ a ) + B_2 \sin ( κ a )} \label{4.15B} \end{align}
We can combine Equations \ref{4.15A} and \ref4.15B} to a single one by equating the right-hand sides. After deleting the common factor κ, and multiplying with the denominators we find
[ A_2 \cos ( κ a ) + B_2 \sin ( κ a ) ] [ A_2 \sin ( κ a ) − B_2 \cos ( κ a ) ] = [ A_2 \sin ( κ a ) + B_2 \cos ( κ a ) ] [ A_2 \cos ( κ a ) − B_2 \sin ( κ a ) ] , \label{4.16}
which simplifies to
A_2 B_2 = 0 \label{4.17}
We thus have two families of solutions, those characterized by B_2= 0 and those that have A_2= 0.


