4.6: A physical system (approximately) described by a square well
( \newcommand{\kernel}{\mathrm{null}\,}\)
After all this tedious algebra, let us look at a possible physical realization of such a system. In order to do that, I shall have to talk a little bit about semi-conductors. A semiconductor is a quantum system where the so-called valence electrons completely fill a valence band, and are separated by a gap from a set of free states in a conduction band. These can both be thought of a continuous set of quantum states. The energy difference between the valence and conduction bands is different for different semi-conductors. This can be used in so-called quantum-well structures, where we sandwich a thin layer of, e.g., GaAs between very thick layers of GaAlAs (Figure 4.6.1).
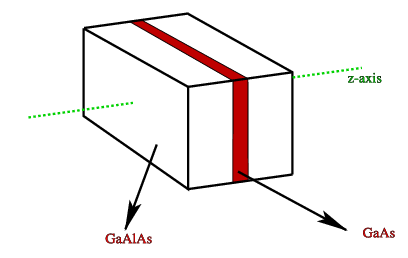
Figure 4.6.1: A schematic representation of a quantum well
Since the gap energy is a lot smaller for GaAs than for GaAlAs, we get the effect of a small square well (in both valence and conduction bands). The fact that we can have a few occupied additional levels in the valence, and a few empty levels in the conduction band can be measured.
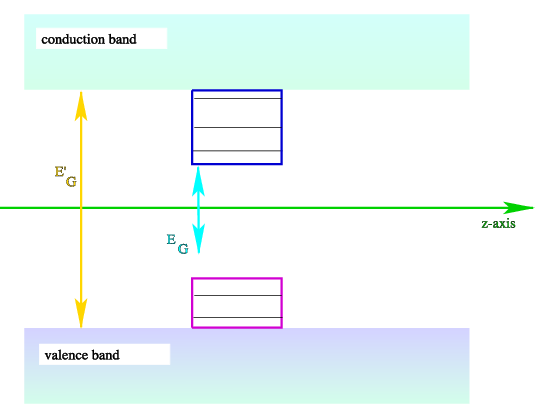
Figure 4.6.2:
The best way to do this, is to shine light on these systems, and see for which frequency we can create a transition (just like in atoms).


