13.1: Bell's Theorem
( \newcommand{\kernel}{\mathrm{null}\,}\)
INTRODUCTION
In 1975 Stapp called Bell's Theorem "the most profound discovery of science." Note that he says science, not physics. I agree with him.
In this document, we shall explore the theorem. We assume some familiarity with the concept of wave-particle duality. We also assume considerable familiarity with the Stern-Gerlach experiment and the concept of a correlation experiment.
A much simpler introduction to the theorem, with some loss of completeness, has been prepared. You may access an html or pdf version with the links to the right.
The origins of this topic is a famous paper by Einstein, Rosen and Podolsky (EPR) in 1935; its title was Can Quantum-Mechanical Description of Physical Reality be Considered Complete? They considered what Einstein called the "spooky action-at-a-distance" that seems to be part of Quantum Mechanics, and concluded that the theory must be incomplete if not outright wrong. As you probably already know, Einstein never did accept Quantum Mechanics. One of his objections was that "God does not play at dice with the universe." Bohr responded: "Quit telling God what to do!"
In the early 1950's David Bohm (not "Bohr") was a young Physics professor at Princeton University. He was assigned to teach Quantum Mechanics and, as is common, decided to write a textbook on the topic; the book is still a classic. Einstein was at Princeton at this time, and as Bohm finished each chapter of the book Einstein would critique it. By the time Bohm had finished the book Einstein had convinced him that Quantum Mechanics was at least incomplete. Bohm then spent many years in search of hidden variables, unobserved factors inside, say, a radioactive atom that determines when it is going to decay. In a hidden variable theory, the time for the decay to occur is not random, although the variable controlling the process is hidden from us. We will discuss Bohm's work extensively later in this document.
In 1964 J.S. Bell published his theorem. It was cast in terms of a hidden variable theory. Since then, other proofs have appeared by d'Espagnat, Stapp, and others that are not in terms of hidden variables. Below we shall do a variation on d'Espagnat's proof that I devised; it was originally published in the American Journal of Physics 50, 811 - 816 (1982).
PROVING BELL'S INEQUALITY
We shall be slightly mathematical. The details of the math are not important, but there are a couple of pieces of the proof that will be important. The result of the proof will be that for any collection of objects with three different parameters, A, B and C:
The number of objects which have parameter A but not parameter B plus the number of objects which have parameter B but not parameter C is greater than or equal to the number of objects which have parameter A but not parameter C.
We can write this more compactly as:
Number(A, not B) + Number(B, not C) greater than or equal to Number(A, not C)
The relationship is called Bell's inequality.
In class I often make the students the collection of objects and choose the parameters to be:
A: male B: height over 5' 8" (173 cm) C: blue eyes
Then the inequality becomes that the number of men students who do not have a height over 5' 8" plus the number of students, male and female, with a height over 5' 8" but who do not have blue eyes is greater than or equal to the number of men students who do not have blue eyes. I absolutely guarantee that for any collection of people this will turn out to be true.
It is important to stress that we are not making any statistical assumption: the class can be big, small or even zero size. Also, we are not assuming that the parameters are independent: note that there tends to be a correlation between gender and height.
Sometimes people have trouble with the theorem because we will be doing a variation of a technique called proof by negation. For example, here is a syllogism:
All spiders have six legs. All six legged creatures have wings. Therefore all spiders have wings
If we ever observe a spider that does not have wings, then we know that at least one and possibly both of the assumptions of the syllogism are incorrect. Similarly, we will derive the inequality and then show an experimental circumstance where it is not true. Thus we will know that at least one of the assumptions we used in the derivation is wrong.
Also, we will see that the proof and its experimental tests have absolutely nothing to do with Quantum Mechanics.
Now we are ready for the proof itself. First, I assert that:
Number(A, not B, C) + Number(not A, B, not C) must be either 0 or a positive integer
or equivalently:
Number(A, not B, C) + Number(not A, B, not C) greater than or equal to 0
This should be pretty obvious, since either no members of the group have these combinations of properties or some members do.
Now we add Number(A, not B, not C) + Number(A, B, not C) to the above expression. The left hand side is:
Number(A, not B, C) + Number(A, not B, not C) + Number(not A, B, not C) + Number(A, B, not C)
and the right hand side is:
0 + Number(A, not B, not C) + Number(A, B, not C)
But this right hand side is just:
Number(A, not C)
since for all members either B or not B must be true. In the classroom example above, when we counted the number of men without blue eyes we include both those whose height was over 5' 8" and those whose height was not over 5' 8".
Above we wrote "since for all members either B or not B must be true." This will turn out to be important.
We can similarly collect terms and write the left hand side as:
Number(A, not B) + Number(B, not C)
Since we started the proof by asserting that the left hand side is greater than or equal to the right hand side, we have proved the inequality, which I re-state:
Number(A, not B) + Number(B, not C) greater than or equal to Number(A, not C)
We have made two assumptions in the proof. These are:
- Logic is a valid way to reason. The whole proof is an exercise in logic, at about the level of the "Fun With Numbers" puzzles one sometimes sees in newspapers and magazines.
- Parameters exist whether they are measured or not. For example, when we collected the terms Number(A, not B, not C) + Number(A, B, not C) to get Number(A, not C), we assumed that either not B or B is true for every member.
APPLYING BELL'S INEQUALITY TO ELECTRON SPIN
Consider a beam of electrons from an electron gun. Let us set the following assignments for the three parameters of Bell's inequality:
A: electrons are "spin-up" for an "up" being defined as straight up, which we will call an angle of zero degrees. B: electrons are "spin-up" for an orientation of 45 degrees. C: electrons are "spin-up" for an orientation of 90 degrees.
Then Bell's inequality will read:
Number(spin-up zero degrees, not spin-up 45 degrees) + Number(spin-up 45 degrees, not spin-up 90 degrees) greater than or equal to Number(spin-up zero degrees, not spin-up 90 degrees)
But consider trying to measure, say, Number(A, not B). This is the number of electrons that are spin-up for zero degrees, but are not spin-up for 45 degrees. Being "not spin-up for 45 degrees" is, of course, being spin-down for 45 degrees.
We know that if we measure the electrons from the gun, one-half of them will be spin-up and one-half will be spin-down for an orientation of 0 degrees, and which will be the case for an individual electron is random. Similarly, if measure the electrons with the filter oriented at 45 degrees, one-half will be spin-down and one-half will be spin-up.
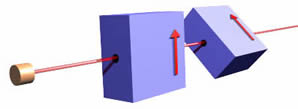 But if we try to measure the spin at both 0 degrees and 45 degrees we have a problem.
But if we try to measure the spin at both 0 degrees and 45 degrees we have a problem.
The figure to the right shows a measurement first at 0 degrees and then at 45 degrees. Of the electrons that emerge from the first filter, 85% will pass the second filter, not 50%. Thus for electrons that are measured to be spin-up for 0 degrees, 15% are spin-down for 45 degrees.
Thus measuring the spin of an electron at an angle of zero degrees irrevocably changes the number of electrons which are spin-down for an orientation of 45 degrees. If we measure at 45 degrees first, we change whether or not it is spin-up for zero degrees. Similarly for the other two terms in this application of the inequality. This is a consequence of the Heisenberg Uncertainty Principle. So this inequality is not experimentally testable.
In our classroom example, the analogy would be that determining the gender of the students would change their height. Pretty weird, but true for measuring electron spin.
However, recall the correlation experiments that we discussed earlier. Imagine that the electron pairs that are emitted by the radioactive substance have a total spin of zero. By this we mean that if the right hand electron is spin-up its companion electron is guaranteed to be spin-down provided the two filters have the same orientation.
 Say in the illustrated experiment the left hand filter is oriented at 45 degrees and the right hand one is at zero degrees. If the left hand electron passes through its filter then it is spin-up for an orientation of 45 degrees. Therefore we are guaranteed that if we had measured its companion electron it would have been spin-down for an orientation of 45 degrees. We are simultaneously measuring the right-hand electron to determine if it is spin-up for zero degrees. And since no information can travel faster than the speed of light, the left hand measurement cannot disturb the right hand measurement.
Say in the illustrated experiment the left hand filter is oriented at 45 degrees and the right hand one is at zero degrees. If the left hand electron passes through its filter then it is spin-up for an orientation of 45 degrees. Therefore we are guaranteed that if we had measured its companion electron it would have been spin-down for an orientation of 45 degrees. We are simultaneously measuring the right-hand electron to determine if it is spin-up for zero degrees. And since no information can travel faster than the speed of light, the left hand measurement cannot disturb the right hand measurement.
So we have "beaten" the Uncertainty Principle: we have determined whether or not the electron to the right is spin-up zero degrees, not spin-up 45 degrees by measuring its spin at zero degrees and its companion's spin at 45 degrees.
Now we can write the Bell inequality as:
Number(right spin-up zero degrees, left spin-up 45 degrees) + Number(right spin-up 45 degrees, left spin-up 90 degrees) greater than or equal to Number(right spin-up zero degrees, left spin-up 90 degrees)
This completes our proof of Bell's Theorem.
The same theorem can be applied to measurements of the polarization of light, which is equivalent to measuring the spin of photon pairs.
The experiments have been done. For electrons the left polarizer is set at 45 degrees and the right one at zero degrees. A beam of, say, a billion electrons is measured to determine Number(right spin-up zero degrees, left spin-up 45 degrees). The polarizers are then set at 90 degrees/45 degrees, another billion electrons are measured, then the polarizers are set at 90 degrees/zero degrees for another billion electrons.
The result of the experiment is that the inequality is violated. The first published experiment was by Clauser, Horne, Shimony and Holt in 1969 using photon pairs. The experiments have been repeated many times since.
The experiments done so far have been for pairs of electrons, protons, photons and ionised atoms. It turns out that doing the experiments for photon pairs is easier, so most tests use them. Thus, in most of the remainder of this document the word "electron" is generic.
Technical note: You may recall from our discussion of the Stern-Gerlach experiment that doing a correlation experiment for electrons with the polarisers at some relative angle is equivalent to doing the experiment for photons with the polarisers at half the relative angle of the electron polarisers. Thus, when we discuss an electron measurement with the polarisers at, say, zero degrees and 45 degrees, for a photon experiment it would be zero degrees and 22.5 degrees.
In the last section we made two assumptions to derive Bell's inequality which here become:
- Logic is valid.
- Electrons have spin in a given direction even if we do not measure it.
Now we have added a third assumption in order to beat the Uncertainty Principle:
- No information can travel faster than the speed of light.
We will state these a little more succinctly as:
- Logic is valid.
- There is a reality separate from its observation
- Locality.
You will recall the we discussed proofs by negation. The fact that our final form of Bell's inequality is experimentally violated indicates that at least one of the three assumptions we have made have been shown to be wrong.
You will also recall that earlier we pointed out that the theorem and its experimental tests have nothing to do with Quantum Mechanics. However, the fact that Quantum Mechanics correctly predicts the correlations that are experimentally observed indicates that the theory too violates at least one of the three assumptions.
Finally, as we stated, Bell's original proof was in terms of hidden variable theories. His assumptions were:
- Logic is valid.
- Hidden variables exist.
- Hidden variables are local.
Most people, including me, view the assumption of local hidden variables as very similar to the assumption of a local reality.
WHAT NOW?
As can be easily imagined, many people have tried to wiggle out of this profound result. Some attempts have critiqued the experimental tests. One argument is that since we set the two polarizers at some set of angles and then collect data for, say, a billion electrons there is plenty of time for the polarizers to "know" each other's orientation, although not by any known mechanism. More recent tests set the orientation of the the polarizers randomly after the electrons have left the source. The results of these tests are the same as the previous experiments: Bell's inequality is violated and the predicted Quantum correlations are confirmed. Still other tests have set the distance between the two polarizers at 11 km, with results again confirming the Quantum correlations.
Another critique has been that since the correlated pairs emitted by the source go in all directions, only a very small fraction of them actually end up being measured by the polarizers. Another experiment using correlated Beryllium atoms measured almost all of the pairs, with results again confirmed the Quantum correlations.
There is another objection to the experimental tests that, at least so far, nobody has managed to get totally around. We measure a spin combination of, say, zero degrees and 45 degrees for a collection of electrons and then measure another spin combination, say 45 degrees and 90 degrees, for another collection of electrons. In our classroom example, this is sort of like measuring the number of men students whose height is not over 5' 8" in one class, and then using another class of different students to measure the number of students whose height is over 5' 8" but do not have blue eyes. The difference is that a collection of, say, a billion electrons from the source in the correlation experiments always behaves identically within small and expected statistical fluctuations with every other collection of a billion electrons from the source. Since that fact has been verified many many times for all experiments of all types, we assume it is true when we are doing these correlation experiments. This assumption is an example of inductive logic; of course we assumed the validity of logic in our derivation.
Sometimes one sees statements that Bell's Theorem says that information is being transmitted at speeds greater than the speed of light. So far I have not seen such an argument that I believe is correct. If we are sitting by either of the polarisers we see that one-half the electrons pass and one-half do not; which is going to be the case for an individual electron appears to be random. Thus, the behavior at our polariser does not allow us to gain any information about the orientation of the other polariser. It is only in the correlation of the electron spins that we see something strange. d'Espagnat uses the word influence to describe what may be traveling at superluminal speeds.
Imagine we take a coin and carefully saw it in half so that one piece is a "heads" and the other is a "tails." We put each half in a separate envelope and carry them to different rooms. If we open one of the envelopes and see a heads, we know that the other envelope contains a tails. This correlation "experiment" corresponds to spin measurements when both polarisers have the same orientation. It is when we have the polarisers at different orientations that we see something weird.
So far we don't know which of the assumptions we made in the proof are incorrect, so we are free to take our pick of one, two or all three. We shall close this section by briefly considering the consequences of discarding the assumption of the validity of logic and then the consequences of discarding the assumption of a reality separate from its observation. In the next section we shall explore the idea of a non-local universe.
What If Logic Is Invalid?
It has been suspected since long before Bell that Quantum Mechanics is in conflict with classical logic. For example, deductive logic is based on a number of assumptions, one of which is the Principle of the Excluded Middle: all statements are either true or false.
But consider the following multiple choice test question:
- The electron is a wave.
- The electron is a particle.
- All of the previous.
- None of the above.
From wave-particle duality we know that both statements 1 and 2 are both sort of true and sort of false. This seems to call into question the Principle of the Excluded Middle. Thus, some people have worked on a multi-valued logic that they hope will be more consistent with the tests of Bells' Theorem and therefore with Quantum Mechanics. Gary Zukav's The Dancing Wu Li Mastershas a good discussion of such a quantum logic; since numerous editions of this book exist and every chapter is numbered 0, I can't supply a more detailed reference.
Mathematics itself can be viewed as just a branch of deductive logic, so if we revise the rules of logic we will need to devise a new mathematics
You may be interested to know that deductive logic has proved that logic is incomplete. The proof was published in 1931 by Gödel; a good reference is Hofstader's Gödel, Escher, Bach. The key to Gödel's work is self-reference; we shall see an example of self-reference in the next sub-section. What he proved was that any mathematics at all, unless it is trivially limited, will contain statements that are neither true nor false but simply unprovable.
|
By self-reference we mean a statement or set of statements that refer to themselves. For example, consider: This statement is false. Note that if this statement is true, then it must be false. If the statement if false, then it must be true. So we have a chain of True » False » True » False .... |

New Yorker, Mar 5, 2001, pg. 78. |
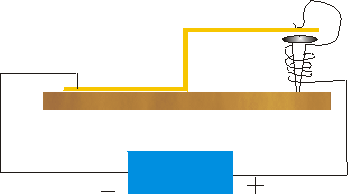 This may remind you a bit of a simple buzzer, such as a door buzzer.
This may remind you a bit of a simple buzzer, such as a door buzzer.
A buzzer is shown to the right. A flexible piece of metal is bent into a double L shape and nailed to a board. A big nail is placed just under the right hand part of the metal, and the metal is adjusted so that it does not quite touch the big nail. A battery is wired in such a fashion that when the the metal Lis at rest, the circuit is just completed, which causes the big nail to become an electromagnet.
This of course pulls the metal down, which breaks the circuit. Thus the metal springs back up, which completes the circuit again, which pulls the metal down, and so on. Thus, if the circuit is closed, it opens, and if the circuit is open, then it is closed. Or, we say we have a chain of Closed » Open » Closed » Open .... The difference between this example and the previous self-referential statement is that here the oscillations in value are occurring in time. You may access a Flash animation of a buzzer by clicking here.
In the late nineteenth century the logician Hilbert used to say "Physics is too important to be left to the physicists." In retaliation, J.A. Wheeler has stated: "Gödel is too important to be left to the mathematicians."
Finally, although deductive logic is fairly well understood, nobody has succeeded in codifying iron-clad rules for inductive logic that work consistently. Mills tried very hard to do this, but the following story by Copi shows one problem:
"A favorite example used by critics of the Method of Agreement is the case of the Scientific Drinker, who was extremely fond of liquor and got drunk every night of the week. He was ruining his health, and his few remaining friends pleaded with him to stop. Realizing himself that he could not go on, he resolved to conduct a careful experiment to discover the exact cause of his frequent inebriations. For five nights in a row he collected instances of a given phenomenon, the antecedent circumstances being respectively scotch and soda, bourbon and soda, brandy and soda, rum and soda, and gin and soda [ugh!]. Then using the Method of Agreement he swore a solemn oath never to touch soda again!"
Reference: I. Copi, Introduction to Logic, 2nd ed., (Macmillan, New York, 1961), pp 394-395.
Note the "hidden variable" in the above story.
What If There Is No Reality Separate From Its Observation?
As we have seen, the title of this sub-section is very similar to asking what are the consequences of having no hidden variables. We shall concentrate on the first form of the question.
You may have already noticed that the question is a variation on the old philosophical saw regarding a tree that falls in the forest with nobody there to hear the sound.
A conflict between the assumption of reality and Quantum Mechanics has been suspected long before Bell. For example, in referring to the trajectory of the electron in, say, the double slit experiment Heisenberg stated "The path of the electron comes into existence only when we observe it."
People have long known that any measurement disturbs the thing being measured. A crucial assumption of classical sciences has been that at least in principle the disturbance can be made so small that we can ignore it. Thus, when an anthropologist is studying a primitive culture in the field, she assumes that her presence in the tribe is having a negligible effect on the behavior of the members. Sometimes we later discover that all she was measuring was the behavior of the tribe when it was being observed by the anthropologist.
Nonetheless, classically we assume a model where we, as observers, are behind a pane of glass where see what is going on "out there." Now we suggest that the pane of glass has been shattered. Wheeler suggests that we should drop the word observerentirely, and replace it with participator.
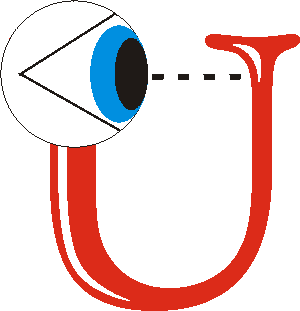 Wheeler has thought more deeply on the consequences of a participatory universe than anybody. He devised the figure to the right, whose caption is:
Wheeler has thought more deeply on the consequences of a participatory universe than anybody. He devised the figure to the right, whose caption is:
“Symbolic representation of the Universe as a self-excited system brought into being by ‘self-reference’. The universe gives birth to communicating participators. Communicating participators give meaning to the universe … With such a concept goes the endless series of receding reflections one sees in a pair of facing mirrors.”
Reference: J.A. Wheeler in Isham et al., eds, Quantum Gravity (Clarendon, Oxford, 1975), pg. 564-565. The colors were used by Wheeler in a colloquium in the Dept. of Physics, Univ. of Toronto some years ago.
You may have noticed a similarity between this view of Quantum Mechanics and the Idealist philosophy of Bishop Berkeley. Berkeley would likely have been very happy about Bell's Theorem. Dr. Johnson was, of course, opposed to Berkeley and used to argue against his philosophy by bellowing "I refute it thus!" while kicking a large rock. Apparently Johnson found sufficient comfort from his argument that he didn't mind hurting his foot.
d'Espagnat also tends to believe that the reality assumption is incorrect. Thus he wrote: "The doctrine that the world is made up of objects whose existence is independent of human consciousness turns out to be in conflict with quantum mechanics and with facts established by experiment."
In a participatory universe, I can argue that you owe your objective existence to my kind intervention in allowing you into my own consciousness. Thus, there is an inherent solipsism in this position. Wigner was one of many who was greatly troubled by this.
NON-LOCALITY AND DAVID BOHM
Recall that David Bohm set off in the early 1950's on a quest for the hidden variables. Nobody has explored the consequences of such variables being non-local more deeply than Bohm, and in the first sub-section below we shall discuss some of his work on this topic. In the next sub-section we shall discuss his later thinking about the nature of the world.
The Implicate Order
A good reference for the material of this sub-section is David Bohm, Wholeness and the Implicate Order. Although very deep the book is not technical except for Chapter 4, which I think should not have been included.
Bohm called our everyday world of space, time and causality the explicate order. He proposed that underlying this everyday world is an interconnected one which he calls the implicate order. He used a number of analogies and images to discuss these two orders.
In one analogy he imagined a large cylindrical glass container of glycerine mounted on a turntable. We place a spot of black ink in the glycerine. We slowly rotate the container, and the ink gradually disperses throughout the glycerine. If we slowly rotate the cylinder in the opposite direction the spot of ink gradually re-forms. When the ink is dispersed it is in an implicate state: it exists throughout the glycerine. When the ink is a spot it is explicate: it exists in one part of the glycerine but not in the other parts. If we continue rotating the cylinder in this opposite direction the spot disperses again.
We extend the image as follows. We place the spot of ink as before. We slowly rotate the cylinder one revolution, and the ink has begun to disperse. We place a second spot of ink just beside where the first spot was, and rotate for one more revolution. A third spot is placed beside where the second was, one more revolution, and we continue this for a few spots. Then we continue slowly rotating the cylinder until all the ink is fully dispersed. When we reverse the direction of rotation we see the last spot coalesce, then the next to last one right beside the last one, and so on. We could interpret what we are seeing as a single spot of ink that is moving. So in the implicate fully dispersed state we have enfolded the motion in space and time of an object throughout the glycerine. Reversing the rotation unfolds the reality back into space and time.
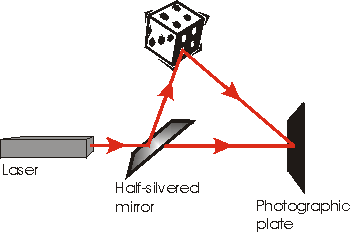 Another analogy is a hologram. As shown to the right, to make a hologram we split a laser beam into two pieces with a half-silvered mirror. One piece goes straight to a photographic plate, the other bounces off the object and then goes to the plate. In order to reconstruct the image of the object we shine a laser beam through the developed plate: the three-dimensional image appears. Note that in some sense the hologram on the plate is an interference pattern between the beam that has experienced the thing and the beam that experienced no-thing.
Another analogy is a hologram. As shown to the right, to make a hologram we split a laser beam into two pieces with a half-silvered mirror. One piece goes straight to a photographic plate, the other bounces off the object and then goes to the plate. In order to reconstruct the image of the object we shine a laser beam through the developed plate: the three-dimensional image appears. Note that in some sense the hologram on the plate is an interference pattern between the beam that has experienced the thing and the beam that experienced no-thing.
One characteristic of a hologram is that down to at least a few grains of the silver in the plate, each piece of the plate contains the entire image. If we cut the plate in half we do not lose half the image; instead we lose resolution and the image becomes more fuzzy. Thus each piece of the plate contains the entire space of the object in an enfolded way; this is an analogy to the implicate order. When we reconstruct the image, we have unfolded the implicate order into an explicate one.
There are "multiplexed" holograms that contain time information too. If the object is moving, we rotate the photographic plate. When we reconstruct the image if we look from different angles we see the object's motion. Here the object's time behavior is also enfolded into the totality.
We see that in the implicate order there is no spatial or time separation. Thus it is a non-local order.
Here is another image used by Bohm:
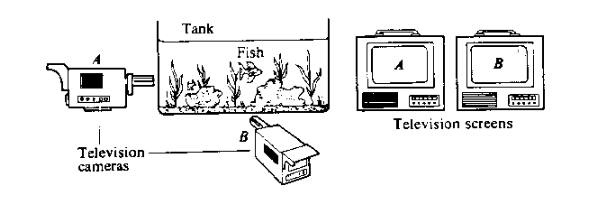
He comments: "The images on the screens are two dimensional projections (or facets) of a three dimensional reality. ... Yet, since these projections exist only as abstractions, the three-dimensional reality is neither of these. ... What is actually found [in the experimental tests of Bell's theorem] is that the behavior of the two [electrons] is correlated in a way that is rather similar to that of the two television images of the fish, as described earlier. Thus ... each electron acts as if it were a projection of a higher-dimensional reality. ... What we are proposing here is that the quantum property of a non-local, non-causal relation of distant elements may be understood through an extension of the notion described above." -- pg. 187-188.
The following table compares the explicate and implicate order:
| Explicate | Implicate |
|---|---|
| parts make up the whole | whole makes up the parts |
| spatial separation | holographic |
| describable | "finger pointing to the moon" |
| things exist | 'thing' and 'no-thing' interfere |
| "ten thousand things" | illusion |
| spacetime | spectra |
Given the unbroken wholeness of the implicate order, Bohm asked why our thought is so dominated by fragmentation.
"... fragmentation is continually being brought about by the almost universal habit of taking the content of our thought for `a description of the world as it is'." -- pg. 3.
He also wrote about what to do about this:
"[Meditation] is particularly important because ... the illusion that the self and the world are broken into fragments originates in the kind of thought that goes beyond its proper measure and confuses its own product with the same independent reality. To end this illusion requires insight, not only into the world as a whole, but also into how the instrument of thought is working." -- pg. 25.
Bohm's Ontology of Quantum Mechanics
In philosophy, epistemology is the study of what we know and how we know it; this is as opposed to ontology which studies what actually exists. Most interpretations of Quantum Mechanics have been developed by people sympathetic to the idea of a participatory universe; we discussed this idea above. Therefore, these interpretations are essentially epistemology.
For Bohm, this wasn't good enough. He developed an ontology in his later years. His master work, The Undivided Universe, was written with his collaborator B.J. Hiley and published in 1993. It is written for physicists, and I can't really recommend it to a non-technical audience. Here we shall briefly explore some of the conclusions from this book.
Essentially, Bohm and his school re-interpreted the mathematics of Quantum Mechanics and extracted a part of the equation which they called the quantum potential. The quantum potential is non-local, and is responsible for all the non-local effects predicted by the theory.
The quantum potential guides, say, the path of an electron in a way similar to the way a radio beacon can guide an airplane coming in for a landing at the airport. It is the jets, ailerons, rudder, etc. on the plane that mechanically determines where the plane is going, but the beacon guides the way.
In Bohm's ontology electrons really are particles. For the case of, for example, the double slit experiment for electrons, each electron goes through either the upper slit or the lower slit; it has a definite path independent of its observation. However, the quantum potential is different depending on whether the other slit is open or closed; since this potential is non-local it can instantaneously change if the other slit is opened or closed. Thus the electron paths are different depending on whether or not the other slit is open.
You may recall that for a chaotic system, very small changes in initial conditions leads to radically different trajectories; you may read more about this here. It turns out that for the double slit experiment for electrons, the motion of the electron after it has passed the slits is chaotic in just this sense. Thus, even small thermal fluctuations in the electron's interaction with the slits cause the electron's future motion to be unknowable to us, even though it is strictly deterministic. Thus it seems to us that the path of the electron is random, although in reality it is not.
We call Physics before Quantum Mechanics classical; thus the theories of relativity are classical. Usually we characterise a classical theory as one that includes observers and strict determinism, while a non-classical theory has participators and randomness. If Bohm's interpretation is correct we need to change the way we characterise the distinction. A classical theory is local, while a non-classical one is non-local; both are strictly deterministic and have observers. Bohm had some hope that his ontology would have experimentally testable consequences, although no such experiments have yet been done.
You may wish to know that in Bohm's analysis the so-called photon is not a particle; it is an electromagnetic field whose particle-like behavior arises because of its interaction with the quantum potential.
Note that in this work, then, Bohm has finally identified the hidden variable he searched for for so many years: it is the quantum potential.
The non-locality of this potential led Bohm to invoke an image very similar to the one Wheeler used above in his discussion of the universe as a self-excited system:
"Classical physics provided a mirror that reflected only the objective structure of the human being who was the observer. There is no room in this scheme for his mental process which is thus regarded as separate or as a mere 'epiphenomenon' of the objective processes. ... [Through the] mirror [of quantum physics] the observer sees 'himself' both physically and mentally in the larger setting of the universe as a whole. ... More broadly one could say that through the human being, the universe is making a mirror to observe itself." -- Bohm and Hiley, The Undivided Universe, pg. 389
A colleague remarked to me that Bohm's heroic attempts to keep a reality separate from its observation, in this "final" form, is worse than the alternative of not having a reality. I don't know about the word worse, but after Bell's theorem something has to give, whether it is reality, locality and/or logic itself.
There are still some unresolved issues regarding Bohm's ontology. For example, as discussed elsewhere, the standard planetary model of the atom where the electrons orbit the nucleus just as the planets orbit the Sun is impossible, because according to classical electromagnetism such an electron is in a state of non-uniform accelerated motion and must radiate away its energy, causing it to spiral into the nucleus. However, when we think about the electron in its wave aspect, then when the waves are in a standing wave pattern, this corresponds to the allowed orbits of the Bohr model and the electrons do not radiate.
When the idea of treating the electron as a wave is fully developed by Quantum Mechanics, the orbits are more complicated then indicated in the document referenced in the previous paragraph.
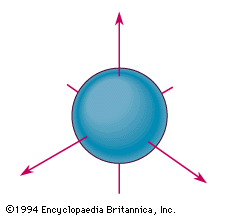 To the right we show the "wave function" for the electron in its ground state orbital. It can be seen that it is spherically symmetric. In an earlier discussion we called this the orbit for which the quantum number n is equal to 1.
To the right we show the "wave function" for the electron in its ground state orbital. It can be seen that it is spherically symmetric. In an earlier discussion we called this the orbit for which the quantum number n is equal to 1.
In Bohm's ontology, the electron is a particle. But for this orbit the electron is stationary, with the electric force trying to pull it into the proton being just balanced by the quantum potential. Thus, this electron will certainly not radiate away energy.
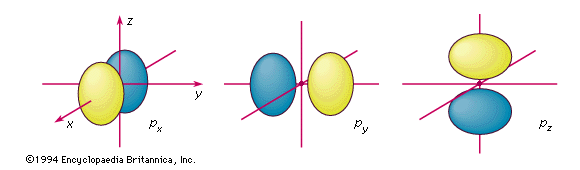
For the state with principle quantum number 2, there is a spherically symmetric wave function that looks just like the one shown before for n = 1. But there are also three other orbitals, which look as shown above.
For the first two of these "p" orbitals, the electrons are moving and accelerating and would be expected to radiate away energy. The last pz orbital turns out to represent an electron that is stationary.
This is clearly in conflict with the fact that the electrons in the atom do not radiate energy except when they change from one allowed orbit to another allowed orbit.
In fact, this difficulty manifests in another form in the double slit experiment for electrons. If the electron is a particle that changes its trajectory when it goes through the slits, it too should radiate away energy. One of Bohm's colleagues, Vigier, recently said that the wavelength of this radiation is very large and so the energy loss is negligible; some people believe that Vigier is wrong. Work on this problem is currently being pursued; one of the people working on it is Professor John Sipe of this Department. I became aware of this controversy in attempting to find the answer to a question asked by former JPU200Y student Sharmilla Reid.
CELLULAR AUTOMATA
A cellular automaton provides another approach to the study of the emergence of structures based on rules.
One of the best known automata is the Game of Life, devised by John Conway in 1970. This example is played on a large checkerboard-like grid. One starts with a configuration of cells on the board that are populated, and then calculates the population in succeeding generations using three simple rules:
- Birth: an unoccupied cell with exactly 3 occupied neighbors will be populated in the next generation.
- Survival: an occupied cell with 2 or 3 occupied neighbors will be populated in the next generation.
- Death: in all other cases a cell is unoccupied in the next generation.
Despite the simplicity of the rules, truly amazing patterns of movement, self-organising complexity, and more arise in this game.
You can play an animation of the game of life on the web
- Click on the Step button to step from generation to generation. In this mode the number of occupied neighbors of each cell is shown.
- Click on Play to resume playing the animation.
There are many resources available on the web to explore this fascinating "game" in more detail.
It has been proposed that these sorts of automata may form a useful model for how the universe really works. Contributors to this idea include Konrad Zuse in 1967, Edward Fredkin in the early 1980's, and more recently Stephen Wolfram in 2002. Wolfram's work in particular is the outcome of nearly a decade of work, which is described in a mammoth 1200 page self-published book modestly titled A New Kind of Science.
There are two key features of cellular automata that are relevant for this discussion:
- The rules are always strictly deterministic.
- The evolution of a cell depends only on its nearest neighbors.
This seems to put a cellular automaton model of Physics in conflict with Bell's Theorem, which asserts that a logical local deterministic model of the universe can not be correct.
Advocates of the cellular automaton model attempt to argue that there is no essential conflict, just an apparent one. Arguments include:
- That the apparent randomness of quantum phenomena is only pseudo-random. To me, they seem to be re-introducing the idea of hidden variables via the back door. Plamen Petrov in one of the proponents of this argument.
- That there is some sort of higher-dimensional thread outside of the normal four dimensions of space and time. This "thread" will somehow allow for super-luminal connections. Wolfram and others have proposed this idea.
- Other Wolfram supporters have argued that the speed of light is or can be much greater than the "usual" value that we are used to. Whether or not it needs to be infinite is not clear.
In the previous Bohm's Ontology of Quantum Mechanics sub-section, we saw that Bohm's attempt to keep causality ended up with a totally non-local mechanism encapsulated in a Quantum Potential. Even there, we saw at the end that there are serious problems with the model.
It may be that there are even more serious problems with the Cellular Automaton model for the way the universe works. The controversy continues to be very active as of this writing (Spring, 2003). A semi-random list of further readings is:
- arxiv.org/PS_cache/quant-ph/pdf/0206/0206089.pdf
- http://www.math.usf.edu/~eclark/ANKOS_reviews.html
- http://digitalphysics.org/Publications/Petrov/Pet02m/Pet02m.htm
FINALLY ...
Einstein died many years ago, and so is not here to defend himself against claims of what he would or would not do today. Nonetheless, I tend to think that if he were alive today, Bell's theorem would force him to accept Quantum Mechanics.
Contributor
David M. Harrison, Department of Physics, University of Toronto, harrison@physics.utoronto.ca.

