13.18: Wave-Particle Duality

QUOTABLE QUOTES

1. Common sense is the deposit of prejudice laid down in the mind before the age of 18. A. Einstein

2. God is a mathematician of a very high order and He used very advanced mathematics in constructing the Universe. P.A.M. Dirac

3. If you are not confused by Quantum Physics then you haven't really understood it. N.Bohr

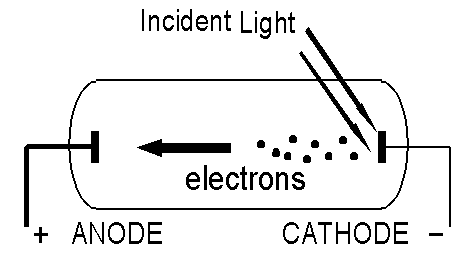
What is the Photo-Electric Effect?

In the Photo-Electric effect, a metal is illuminated with light. Under certain circumstances, electrons are emitted from the illuminated surface. We can vary the intensity of the light and its frequency (its colour).

 

Expectations of Classical Physics.

These expectations are based on the belief that light is an electromagnetic wave; if we increase the intensity of the light this is equivalent to increasing the amplitude of the oscillating electric field of which the light wave is composed. Since the energy of the light beam is spread uniformly over the beam, it is transferred continuously to the electrons, which require a certain minimum of energy to escape the attractive forces of the metal. In the following, "The maximum energy of the electrons" means "The energy of the most energetic electrons".

• c. There may be a time delay between the switching on of the light and the appearance of the first electrons; the lower the light intensity, the longer will be this time delay.

Experimental Observations.

• c. No matter how weak the light, as long as its frequency is above the threshold frequency, the emission of electrons starts IMMEDIATELY the light is switched on.

(In case you were wondering; an increase in the light intensity increases the number of electrons emitted per second, while leaving the energy of each electron unchanged).

Einstein's Explanation.

• c. The interaction between a photon and an electron in the metal is a unique, elemental act, in which the photon can give up some, or all of its energy to the electron, which then might have enough energy to escape from the metal.

Why does this explain the observations?

The electron is kept in the metal by the electric forces, and can only escape if a certain minimum amount of energy is given to it. If the photon energy (i.e. frequency) is too low to overcome this attractive force between the electrons and the metal, the electron can't escape. Thus the frequency of the photon must be above a certain value (which depends on the particular metal). Once we are above this threshold, the photon either hits an electron or it doesn't. If it does, and if enough energy is transferred to the the electron from the photon, the electron will have enough energy to escape IMMEDIATELY, with no time delay. Also, if we increase the energy of the photon by increasing its frequency, the electrons which interact with these electrons can come off with increased energy).

Einstein's conjecture that the energy of a photon is proportional to its frequency can be written E_photon = h f ; here h is Planck's constant.

Particles are also Waves.

The great success of Einstein's theory for the photoelectric effect stimulate de Broglie to postulate in his Ph.D. thesis at the University of Paris, that particles might exhibit wave-like properties. Starting from Einstein's relation, E_photon = h f and using the relation given by Maxwell's equations for the momentum of a light wave, E_light = pc (where p is the momentum of the light, and c is the speed of light), de Broglie derived the expression p =h/, where is the wavelength of light; he proposed that this relation could be taken over to refer to particles, whose "wavelength" (whatever that means!) would be given by = h/p.

[Note the deliciously schizophrenic appearance of these formulae; on the right hand side there is a "particle" property - energy or momentum, while on the right hand side there is a "wave" property - frequency or wavelength.]

How could these particle wavelengths be observed? Remember that one identifying feature of waves is their ability to interfere, as in the double slit experiment. However, for electrons, for instance, this wavelength turns out to be very small. Now remember (see Waves) that wave effects (i.e. diffraction effects or interference) are difficult to see if we use measuring devices which are much larger than the wavelengths involved. So it was not surprising that the first confirmation of de Broglie's apparently fantastic proposal should find experimental support in the study of the interaction of electrons with metals. For the regular planes of atoms which are found crystals turn out to be just of the correct order of magnitude to allow observation of interference effects of electrons which are being reflected from metal crystal surfaces. In fact such crystal planes had already been used to show the effects of interference for X-rays - which are just very short wavelength electromagnetic waves; the wavelength of X-rays is around a few Angstroms - 1A = 10^-10m - so we need a "diffraction grating" which has line spacing between the slits of the same order of magnitude as this wavelength, and crystal planes do the job!

In 1927, three years after de Broglie's proposal, Davisson and Germer, working at Bell Labs in the US, and, independently G.P. Thomson working at Cambridge University, observed interference patterns in the scattering of electrons. The "wavelength" of the electrons, calculated from the observed interference patterns, agreed exactly with de Broglie's formula.

Author

David M. Harrison, Department of Physics, University of Toronto, [e-mail].