1.5: The Equivalence Principle (Part 1)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Proportionality of Inertial and Gravitational Mass
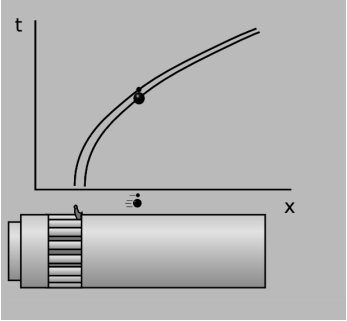
What physical interpretation should we give to the “lines” described in ordered geometry? Galileo described an experiment (which he may or may not have actually performed) in which he simultaneously dropped a cannonball and a musket ball from a tall tower. The two objects hit the ground simultaneously, disproving Aristotle’s assertion that objects fell at a speed proportional to their weights. On a graph of spacetime with x and t axes, the curves traced by the two objects, called their world-lines, are identical parabolas. (The paths of the balls through x − y − z space are straight, not curved.) One way of explaining this observation is that what we call “mass” is really two separate things, which happen to be equal. Inertial mass, which appears in Newton’s a = Fm, describes how difficult it is to accelerate an object. Gravitational mass describes the strength with which gravity acts. The cannonball has a hundred times more gravitational mass than the musket ball, so the force of gravity acting on it is a hundred times greater. But its inertial mass is also precisely a hundred times greater, so the two effects cancel out, and it falls with the same acceleration. This is a special property of the gravitational force. Electrical forces, for example, do not behave this way. The force that an object experiences in an electric field is proportional to its charge, which is unrelated to its inertial mass, so different charges placed in the same electric field will in general have different motions.
Geometrical Treatment of Gravity
Einstein realized that this special property of the gravitational force made it possible to describe gravity in purely geometrical terms. We define the world-lines of small objects9 acted on by gravity to be the lines described by the axioms of the geometry. Since we normally think of the “lines” described by Euclidean geometry and its kin as straight lines, this amounts to a redefinition of what it means for a line to be straight. By analogy, imagine stretching a piece of string taut across a globe, as we might do in order to plan an airplane flight or aim a directional radio antenna. The string may not appear straight as viewed from the three-dimensional Euclidean space in which the globe is embedded, but it is as straight as possible in the sense that it is the path followed by a radio wave,10 or by an airplane pilot who keeps her wings level and her rudder straight. The world-“line” of an object acted on by nongravitational forces is not considered to be a straight “line” in the sense of O1-O4. When necessary, one eliminates this ambiguity in the overloaded term “line” by referring to the lines of O1-O4 as geodesics. The world-line of a low-mass object acted on only by gravity is one type of geodesic.11
Notes
9 The reason for the restriction to small objects is essentially gravitational radiation. The object should also be electrically neutral, and neither the object nor the surrounding spacetime should contain any exotic forms of negative energy. This is discussed in more detail later. See also problem 1.
10 Radio waves in the HF band tend to be trapped between the ground and the ionosphere, causing them to curve over the horizon, allowing long-distance communication.
11 For more justification of this statement, see section 9, problem 1.
We can now see the deep physical importance of statement O1, that two events determine a line. To predict the trajectory of a golf ball, we need to have some initial data. For example, we could measure event A when the ball breaks contact with the club, and event B an infinitesimal time after A.12 This pair of observations can be thought of as fixing the ball’s initial position and velocity, which should be enough to predict a unique world-line for the ball, since relativity is a deterministic theory. With this interpretation, we can also see why it is not necessarily a disaster for the theory if O1 fails sometimes. For example, event A could mark the launching of two satellites into circular orbits from the same place on the Earth, heading in opposite directions, and B could be their subsequent collision on the opposite side of the planet. Although this violates O1, it doesn’t violate determinism. Determinism only requires the validity of O1 for events infinitesimally close together. Even for randomly chosen events far apart, the probability that they will violate O1 is zero.
Note
Regarding infinitesimals, see Example 3.
Eötvös Experiments
Einstein’s entire system breaks down if there is any violation, no matter how small, of the proportionality between inertial and gravitational mass, and it therefore becomes very interesting to search experimentally for such a violation. For example, we might wonder whether neutrons and protons had slightly different ratios of gravitational and inertial mass, which in a Galileo-style experiment would cause a small difference between the acceleration of a lead weight, with a large neutron-to-proton ratio, and a wooden one, which consists of light elements with nearly equal numbers of neutrons and protons. The first high-precision experiments of this type were performed by Eötvös around the turn of the twentieth century, and they verified the equivalence of inertial and gravitational mass to within about one part in 108. These are generically referred to as Eötvös experiments.

Figure 1.5.5 below shows a strategy for doing Eötvös experiments that allowed a test to about one part in 1012. The top panel is a simplified version. The platform is balanced, so the gravitational masses of the two objects are observed to be equal. The objects are made of different substances. If the equivalence of inertial and gravitational mass fails to hold for these two substances, then the force of gravity on each mass will not be exact proportion to its inertia, and the platform will experience a slight torque as the earth spins.
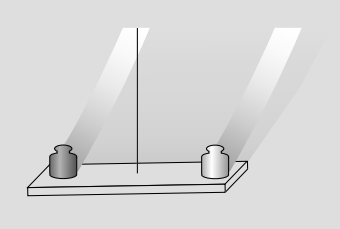
Figure 1.5.5: An Eötvös experiment. Top: simplified version. Bottom: realistic version by Braginskii and Panov. (Drawing after Braginskii and Panov.)
The bottom panel shows a more realistic drawing of an experiment by Braginskii and Panov.13 The whole thing was encased in a tall vacuum tube, which was placed in a sealed basement whose temperature was controlled to within 0.02 °C. The total mass of the platinum and aluminum test masses, plus the tungsten wire and the balance arms, was only 4.4 g. To detect tiny motions, a laser beam was bounced off of a mirror attached to the wire. There was so little friction that the balance would have taken on the order of several years to calm down completely after being put in place; to stop these vibrations, static electrical forces were applied through the two circular plates to provide very gentle twists on the ellipsoidal mass between them.
In the 45 years since Braginskii and Panov’s work, improvements have been made in more direct experimental tests of the equivalence principle, in which the test masses simply free-fall. The best earthbound experiment of this type14 has given a bound of 10−9, while a new experiment in orbit15 has tightened this to 10−14.
Equivalence of Gravitational Fields and Accelerations
One consequence of the Eötvös experiments’ null results is that it is not possible to tell the difference between an acceleration and a gravitational field. At certain times during Betty’s field trip, she feels herself pressed against her seat, and she interprets this as evidence that she’s in a space vessel that is undergoing violent accelerations and decelerations. But it’s equally possible that Tutorbot has simply arranged for her capsule to be hung from a rope and dangled into the gravitational field of a planet. Suppose that the first explanation is correct. The capsule is initially at rest in outer space, where there is no gravity. Betty can release a pencil and a lead ball in the air inside the cabin, and they will stay in place. The capsule then accelerates, and to Betty, who has adopted a frame of reference tied to its deck, ceiling and walls, it appears that the pencil and the ball fall to the deck. They are guaranteed to stay side by side until they hit the deckplates, because in fact they aren’t accelerating; they simply appear to accelerate, when in reality it’s the deckplates that are coming up and hitting them. But now consider the second explanation, that the capsule has been dipped into a gravitational field. The ball and the pencil will still fall side by side to the floor, because they have the same ratio of gravitational to inertial mass.
The Equivalence Principle
This leads to one way of stating a central principle of relativity known as the equivalence principle: Accelerations and gravitational fields are equivalent. There is no experiment that can distinguish one from the other.16
Note
This statement of the equivalence principle is summarized, along with some other forms of it to be encountered later.
To see what a radical departure this is, we need to compare with the completely different picture presented by Newtonian physics and special relativity. Newton’s law of inertia states that “Every object perseveres in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed thereon.”17 Newton’s intention here was to clearly state a contradiction of Aristotelian physics, in which objects were supposed to naturally stop moving and come to rest in the absence of a force. For Aristotle, “at rest” meant at rest relative to the Earth, which represented a special frame of reference. But if motion doesn’t naturally stop of its own accord, then there is no longer any way to single out one frame of reference, such as the one tied to the Earth, as being special. An equally good frame of reference is a car driving in a straight line down the interstate at constant speed. The earth and the car both represent valid inertial frames of reference, in which Newton’s law of inertia is valid. On the other hand, there are other, noninertial frames of reference, in which the law of inertia is violated. For example, if the car decelerates suddenly, then it appears to the people in the car as if their bodies are being jerked forward, even though there is no physical object that could be exerting any type of forward force on them. This distinction between inertial and noninertial frames of reference was carried over by Einstein into his theory of special relativity, published in 1905.
Note
paraphrased from a translation by Motte, 1729
But by the time he published the general theory in 1915, Einstein had realized that this distinction between inertial and noninertial frames of reference was fundamentally suspect. How do we know that a particular frame of reference is inertial? One way is to verify that its motion relative to some other inertial frame, such as the Earth’s, is in a straight line and at constant speed. But how does the whole thing get started? We need to bootstrap the process with at least one frame of reference to act as our standard. We can look for a frame in which the law of inertia is valid, but now we run into another difficulty. To verify that the law of inertia holds, we have to check that an observer tied to that frame doesn’t see objects accelerating for no reason. The trouble here is that by the equivalence principle, there is no way to determine whether the object is accelerating “for no reason” or because of a gravitational force. Betty, for example, cannot tell by any local measurement (i.e., any measurement carried out within the capsule) whether she is in an inertial or a noninertial frame.


We could hope to resolve the ambiguity by making non-local measurements instead. For example, if Betty had been allowed to look out a porthole, she could have tried to tell whether her capsule was accelerating relative to the stars. Even this possibility ends up not being satisfactory. The stars in our galaxy are moving in circular orbits around the galaxy. On an even larger scale, the universe is expanding in the aftermath of the Big Bang. It spent about the first half of its history decelerating due to gravitational attraction, but the expansion is now observed to be accelerating, apparently due to a poorly understood phenomenon referred to by the catch-all term “dark energy.” In general, there is no distant background of physical objects in the universe that is not accelerating.
Lorentz Frames
The conclusion is that we need to abandon the entire distinction between Newton-style inertial and noninertial frames of reference. The best that we can do is to single out certain frames of reference defined by the motion of objects that are not subject to any nongravitational forces. A falling rock defines such a frame of reference. In this frame, the rock is at rest, and the ground is accelerating. The rock’s world-line is a straight line of constant x = 0 and varying t. Such a free-falling frame of reference is called a Lorentz frame. The frame of reference defined by a rock sitting on a table is an inertial frame of reference according to the Newtonian view, but it is not a Lorentz frame.
In Newtonian physics, inertial frames are preferable because they make motion simple: objects with no forces acting on them move along straight world-lines. Similarly, Lorentz frames occupy a privileged position in general relativity because they make motion simple: objects move along “straight” world-lines if they have no nongravitational forces acting on them.
Example 1: The artificial horizon
The pilot of an airplane cannot always easily tell which way is up. The horizon may not be level simply because the ground has an actual slope, and in any case the horizon may not be visible if the weather is foggy. One might imagine that the problem could be solved simply by hanging a pendulum and observing which way it pointed, but by the equivalence principle the pendulum cannot tell the difference between a gravitational field and an acceleration of the aircraft relative to the ground — nor can any other accelerometer, such as the pilot’s inner ear.

For example, when the plane is turning to the right, accelerometers will be tricked into believing that “down” is down and to the left. To get around this problem, airplanes use a device called an artificial horizon, which is essentially a gyroscope. The gyroscope has to be initialized when the plane is known to be oriented in a horizontal plane. No gyroscope is perfect, so over time it will drift. For this reason the instrument also contains an accelerometer, and the gyroscope is automatically restored to agreement with the accelerometer, with a time-constant of several minutes. If the plane is flown in circles for several minutes, the artificial horizon will be fooled into indicating that the wrong direction is vertical.
Example 2: no antigravity
This whole chain of reasoning was predicated on the null results of Eötvös experiments. In the Rocky and Bullwinkle cartoons, there is a non-Eötvösian substance called upsidasium, which falls up instead of down. Its ratio of gravitational to inertial mass is apparently negative. If such a substance could be found, it would falsify the equivalence principle. Example 10.

Operational Definition of a Lorentz Frame
We can define a Lorentz frame in operational terms using an idealized variation (Figure 1.5.9) on a device actually built by Harold Waage at Princeton as a lecture demonstration to be used by his partner in crime John Wheeler. Build a sealed chamber whose contents are isolated from all nongravitational forces. Of the four known forces of nature, the three we need to exclude are the strong nuclear force, the weak nuclear force, and the electromagnetic force. The strong nuclear force has a range of only about 1 fm (10−15 m), so to exclude it we merely need to make the chamber thicker than that, and also surround it with enough paraffin wax to keep out any neutrons that happen to be flying by. The weak nuclear force also has a short range, and although shielding against neutrinos is a practical impossibility, their influence on the apparatus inside will be negligible. To shield against electromagnetic forces, we surround the chamber with a Faraday cage and a solid sheet of mu-metal. Finally, we make sure that the chamber is not being touched by any surrounding matter, so that short-range residual electrical forces (sticky forces, chemical bonds, etc.) are excluded. That is, the chamber cannot be supported; it is free-falling.
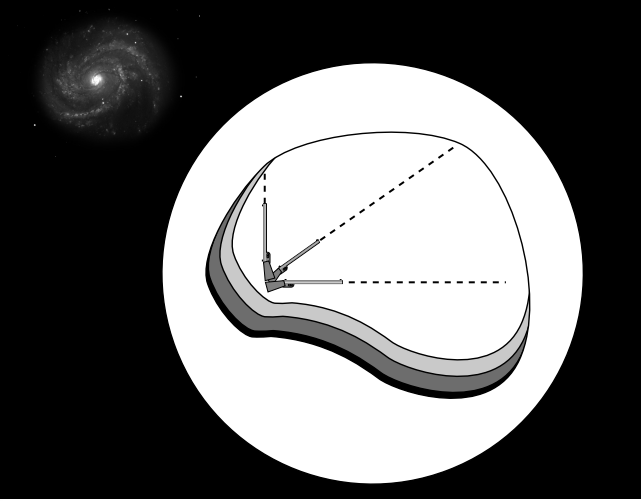
Crucially, the shielding does not exclude gravitational forces. There is in fact no known way of shielding against gravitational effects such as the attraction of other masses or the propagation of gravitational waves. Because the shielding is spherical, it exerts no gravitational force of its own on the apparatus inside.
Inside, an observer carries out an initial calibration by firing bullets along three Cartesian axes and tracing their paths, which she defines to be linear.
We’ve gone to elaborate lengths to show that we can really determine, without reference to any external reference frame, that the chamber is not being acted on by any nongravitational forces, so that we know it is free-falling. In addition, we also want the observer to be able to tell whether the chamber is rotating. She could look out through a porthole at the stars, but that would be missing the whole point, which is to show that without reference to any other object, we can determine whether a particular frame is a Lorentz frame. One way to do this would be to watch for precession of a gyroscope. Or, without having to resort to additional apparatus, the observer can check whether the paths traced by the bullets change when she changes the muzzle velocity. If they do, then she infers that there are velocity-dependent Coriolis forces, so she must be rotating. She can then use flywheels to get rid of the rotation, and redo the calibration.
After the initial calibration, she can always tell whether or not she is in a Lorentz frame. She simply has to fire the bullets, and see whether or not they follow the precalibrated paths. For example, she can detect that the frame has become non-Lorentzian if the chamber is rotated, allowed to rest on the ground, or accelerated by a rocket engine.
It may seem that the detailed construction of this elaborate thought-experiment does nothing more than confirm something obvious. It is worth pointing out, then, that we don’t really know whether it works or not. It works in general relativity, but there are other theories of gravity, such as Brans-Dicke gravity, that are also consistent with all known observations, but in which the apparatus in Figure 1.5.8 doesn’t work. Two of the assumptions made above fail in this theory: gravitational shielding effects exist, and Coriolis effects become undetectable if there is not enough other matter nearby.
Locality of Lorentz Frames
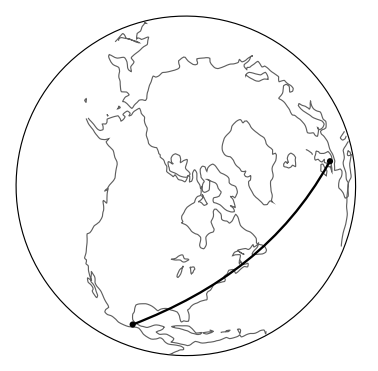
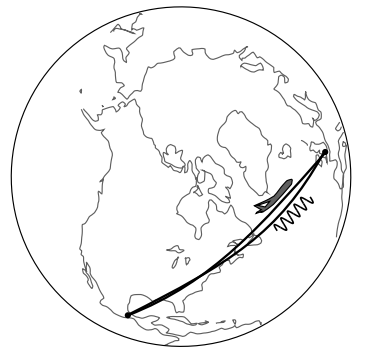
It would be convenient if we could define a single Lorentz frame that would cover the entire universe, but we can’t. In Figure 1.5.9, two girls simultaneously drop down from tree branches — one in Los Angeles and one in Mumbai. The girl free-falling in Los Angeles defines a Lorentz frame, and in that frame, other objects falling nearby will also have straight world-lines. But in the LA girl’s frame of reference, the girl falling in Mumbai does not have a straight world-line: she is accelerating up toward the LA girl with an acceleration of about 2g.
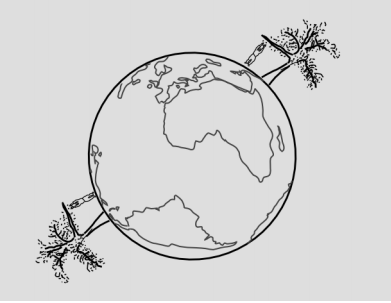
A second way of stating the equivalence principle is that it is always possible to define a local Lorentz frame in a particular neighborhood of spacetime.18 It is not possible to do so on a universal basis.
Note
This statement of the equivalence principle is summarized, along with some other forms of it, in Appendix C.
The locality of Lorentz frames can be understood in the analogy of the string stretched across the globe. We don’t notice the curvature of the Earth’s surface in everyday life because the radius of curvature is thousands of kilometers. On a map of LA, we don’t notice any curvature, nor do we detect it on a map of Mumbai, but it is not possible to make a flat map that includes both LA and Mumbai without seeing severe distortions.
Terminology
The meanings of words evolve over time, and since relativity is now a century old, there has been some confusing semantic drift in its nomenclature. This applies both to “inertial frame” and to “special relativity.”
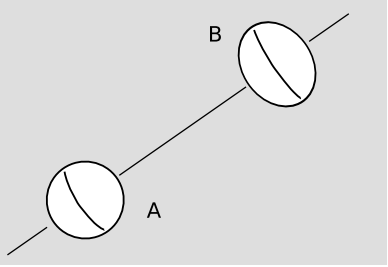
Early formulations of general relativity never refer to “inertial frames,” “Lorentz frames,” or anything else of that flavor. The very first topic in Einstein’s original systematic presentation of the theory19 is an example (Figure 1.5.10) involving two planets, the purpose of which is to convince the reader that all frames of reference are created equal, and that any attempt to make some of them into second-class citizens is invidious. Other treatments of general relativity from the same era follow Einstein’s lead.20 The trouble is that this example is more a statement of Einstein’s aspirations for his theory than an accurate depiction of the physics that it actually implies. General relativity really does allow an unambiguous distinction to be made between Lorentz frames and non-Lorentz frames, as described earlier. Einstein’s statement should have been weaker: the laws of physics (such as the Einstein field equation) are the same in all frames (Lorentz or non-Lorentz). This is different from the situation in Newtonian mechanics and special relativity, where the laws of physics take on their simplest form only in Newton-inertial frames.
Note
Two that I believe were relatively influential are Born’s 1920 Einstein’s Theory of Relativity and Eddington’s 1924 The Mathematical Theory of Relativity. Born follows Einstein’s “Foundation” paper slavishly. Eddington seems only to mention inertial frames in a few places where the context is Newtonian.
Because Einstein didn’t want to make distinctions between frames, we ended up being saddled with inconvenient terminology for them. The least verbally awkward choice is to hijack the term “inertial,” redefining it from its Newtonian meaning. We then say that the Earth’s surface is not an inertial frame, in the context of general relativity, whereas in the Newtonian context it is an inertial frame to a very good approximation. This usage is fairly standard,21 but would have made Newton confused and Einstein unhappy. If we follow this usage, then we may sometimes have to say “Newtonianinertial” or “Einstein-inertial.” A more awkward, but also more precise, term is “Lorentz frame,” as used in this book; this seems to be widely understood.22
The distinction between special and general relativity has undergone a similar shift over the decades. Einstein originally defined the distinction in terms of the admissibility of accelerated frames of reference. This, however, puts us in the absurd position of saying that special relativity, which is supposed to be a generalization of Newtonian mechanics, cannot handle accelerated frames of reference in the same way that Newtonian mechanics can. In fact both Newtonian mechanics and special relativity treat Newtonian-noninertial frames of reference in the same way: by modifying the laws of physics so that they do not take on their most simple form (e.g., violating Newton’s third law), while retaining the ability to change coordinates back to a preferred frame in which the simpler laws apply. It was realized fairly early on23 that the important distinction was between special relativity as a theory of flat spacetime, and general relativity as a theory that described gravity in terms of curved spacetime. All relativists writing since about 1950 seem to be in agreement on this more modern redefinition of the terms.24
In an accelerating frame, the equivalence principle tells us that measurements will come out the same as if there were a gravitational field. But if the spacetime is flat, describing it in an accelerating frame doesn’t make it curved. (Curvature is a physical property of spacetime, and cannot be changed from zero to nonzero simply by a choice of coordinates.) Thus relativity allows us to have gravitational fields in flat space — but only for certain special configurations like this one. Special relativity is capable of operating just fine in this context. For example, Chung et al.25 did a high-precision test of special relativity in 2009 using a matter interferometer in a vertical plane, specifically in order to test whether there was any violation of special relativity in a uniform gravitational field. Their experiment is interpreted purely as a test of special relativity, not general relativity.
Chiao's Paradox
The remainder of this subsection deals with the subtle question of whether and how the equivalence principle can be applied to charged particles. You may wish to skip it on a first reading. The short answer is that using the equivalence principle to make conclusions about charged particles is like the attempts by slaveholders and abolitionists in the 19th century U.S. to support their positions based on the Bible: you can probably prove whichever conclusion was the one you set out to prove.
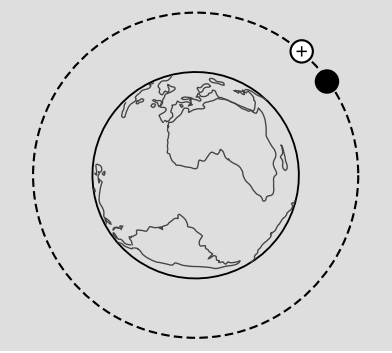
The equivalence principle is not a single, simple, mathematically well defined statement.26 As an example of an ambiguity that is still somewhat controversial, 90 years after Einstein first proposed the principle, consider the question of whether or not it applies to charged particles. Raymond Chiao27 proposes the following thought experiment, which I’ll refer to as Chiao’s paradox. Let a neutral particle and a charged particle be set, side by side, in orbit around the earth. Assume (unrealistically) that the space around the earth has no electric or magnetic field. If the equivalence principle applies regardless of charge, then these two particles must go on orbiting amicably, side by side. But then we have a violation of conservation of energy, since the charged particle, which is accelerating, will radiate electromagnetic waves (with very low frequency and amplitude). It seems as though the particle’s orbit must decay.
Note
A good recent discussion of this is “Theory of gravitation theories: a noprogress report,” Sotiriou, Faraoni, and Liberati, http://arxiv.org/abs/0707.2748
The resolution of the paradox, as demonstrated by hairy calculations28 is interesting because it exemplifies the local nature of the equivalence principle. When a charged particle moves through a gravitational field, in general it is possible for the particle to experience a reaction from its own electromagnetic fields. This might seem impossible, since an observer in a frame momentarily at rest with respect to the particle sees the radiation fly off in all directions at the speed of light. But there are in fact several different mechanisms by which a charged particle can be reunited with its long-lost electromagnetic offspring. An example (not directly related to Chiao’s scenario) is the following.
Note
The first detailed calculation appears to have been by Cécile and Bryce DeWitt, “Falling Charges,” Physics 1 (1964) 3. This paper is unfortunately very difficult to obtain now. A more recent treatment by Grøn and Næss is accessible at arxiv.org/abs/0806.0464v1. A full exposition of the techniques is given by Poisson, “The Motion of Point Particles in Curved Spacetime,” www.livingreviews.org/lrr-2004-6.
Bring a laser very close to a black hole, but not so close that it has strayed inside the event horizon, which is the spherical point of no return from within which nothing can escape. Example 14 gives a plausibility argument based on Newtonian physics that the radius29 of the event horizon should be something like rH=GMc2, and section 6.3 derives the relativistically correct factor of 2 in front, so that rH=2GMc2. It turns out that at r = (32)rH, a ray of light can have a circular orbit around the black hole. Since this is greater than rH, we can, at least in theory, hold the laser stationary at this value of r using a powerful rocket engine. If we point the laser in the azimuthal direction, its own beam will come back and hit it.
Note
Because relativity describes gravitational fields in terms of curvature of spacetime, the Euclidean relationship between the radius and circumference of a circle fails here. The r coordinate should be understood here not as the radius measured from the center but as the circumference divided by 2π.
Since matter can experience a back-reaction from its own electromagnetic radiation, it becomes plausible how the paradox can be resolved. The equivalence principle holds locally, i.e., within a small patch of space and time. If Chiao’s charged and neutral particle are released side by side, then they will obey the equivalence principle for at least a certain amount of time — and “for at least a certain amount of time” is all we should expect, since the principle is local. But after a while, the charged particle will start to experience a back-reaction from its own electromagnetic fields, and this causes its orbit to decay, satisfying conservation of energy. Since Chiao’s particles are orbiting the earth, and the earth is not a black hole, the mechanism clearly can’t be as simple as the one described above, but Grøn and Næss show that there are similar mechanisms that can apply here, e.g., scattering of light waves by the nonuniform gravitational field.
It is worth keeping in mind the DeWitts’ caution that “The questions answered by this investigation are of conceptual interest only, since the forces involved are far too small to be detected experimentally” (see problem 8).
References
13 V.B. Braginskii and V.I. Panov, Soviet Physics JETP 34, 463 (1972).
14 Carusotto et al., “Limits on the violation of g-universality with a Galileotype experiment,” Phys Lett A183 (1993) 355. Freely available online at researchgate.net.
15 Touboul et al., “The MICROSCOPE mission: first results of a space test of the Equivalence Principle,” arxiv.org/abs/1712.01176
19 Einstein, “The Foundation of the General Theory of Relativity,” 1916. An excerpt is given later.
21 Misner, Thorne, and Wheeler, Gravitation, 1973, p. 18
22 ibid, p. 19
23 Eddington, op. cit.
24 Misner, Thorne, and Wheeler, op. cit., pp.163-164. Penrose, The Road to Reality, 2004, p. 422. Taylor and Wheeler, Spacetime Physics, 1992, p. 132. Schutz, A First Course in General Relativity, 2009, pp. 3, 141. Hobson, General Relativity: An Introduction for Physicists, 2005, sec. 1.14.
25 arxiv.org/abs/0905.1929
27 arxiv.org/abs/quant-ph/0601193v7


