5.8: The Geodesic Equation

In this section, which can be skipped at a first reading, we show how the Christoffel symbols can be used to find differential equations that describe geodesics.

Characterization of the Geodesic

A geodesic can be defined as a world-line that preserves tangency under parallel transport, Figure \(\PageIndex{1}\). This is essentially a mathematical way of expressing the notion that we have previously expressed more informally in terms of “staying on course” or moving “inertially.”

Figure \(\PageIndex{1}\): The geodesic, 1, preserves tangency under parallel transport. The non-geodesic curve, 2, doesn’t have this property; a vector initially tangent to the curve is no longer tangent to it when parallel-transported along it.

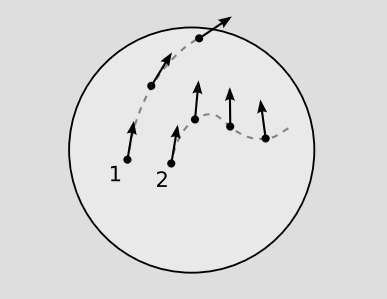
A curve can be specified by giving functions \(x^{\mu} (\lambda)\) for its coordinates, where \(\lambda\) is a real parameter. A vector lying tangent to the curve can then be calculated using partial derivatives, \(T^{\mu} = \frac{\partial x^{\mu}}{\partial \lambda}\). There are three ways in which a vector function of \(\lambda\) could change: (1) it could change for the trivial reason that the metric is changing, so that its components changed when expressed in the new metric; (2) it could change its components perpendicular to the curve; or (3) it could change its component parallel to the curve. Possibility 1 should not really be considered a change at all, and the definition of the covariant derivative is specifically designed to be insensitive to this kind of thing. 2 cannot apply to T^\(\mu\), which is tangent by construction. It would therefore be convenient if T^\(\mu\) happened to be always the same length. If so, then 3 would not happen either, and we could reexpress the definition of a geodesic by saying that the covariant derivative of T^\(\mu\) was zero. For this reason, we will assume for the remainder of this section that the parametrization of the curve has this property. In a Newtonian context, we could imagine the x^\(\mu\) to be purely spatial coordinates, and \(\lambda\) to be a universal time coordinate. We would then interpret T^\(\mu\) as the velocity, and the restriction would be to a parametrization describing motion with constant speed. In relativity, the restriction is that \(\lambda\) must be an affine parameter. For example, it could be the proper time of a particle, if the curve in question is timelike.

Covariant Derivative with Respect to a Parameter

The notation of section 5.6 is not quite adapted to our present purposes, since it allows us to express a covariant derivative with respect to one of the coordinates, but not with respect to a parameter such as \(\lambda\). We would like to notate the covariant derivative of T^\(\mu\) with respect to \(\lambda\) as \(\nabla_{\lambda} T^{\mu}\), even though \(\lambda\) isn’t a coordinate. To connect the two types of derivatives, we can use a total derivative. To make the idea clear, here is how we calculate a total derivative for a scalar function f(x, y), without tensor notation:

\[\frac{df}{d \lambda} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial \lambda} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial \lambda}\]

This is just the generalization of the chain rule to a function of two variables. For example, if \(\lambda\) represents time and f temperature, then this would tell us the rate of change of the temperature as a thermometer was carried through space. Applying this to the present problem, we express the total covariant derivative as

\[\begin{split} \nabla_{\lambda} T^{\mu} &= (\nabla_{\kappa} T^{\mu}) \frac{dx^{\kappa}}{d \lambda} \\ &= (\partial_{\kappa} T^{\mu} + \Gamma^{\mu}_{\kappa \nu} T^{\nu}) \frac{d x^{\kappa}}{d \lambda} \ldotp \end{split}\]

The Geodesic Equation

Recognizing \(\frac{\partial_{\kappa} T^{\mu} dx^{\kappa}}{d \lambda}\) as a total non-covariant derivative, we find

\[\nabla_{\lambda} T^{\mu} = \frac{dT^{\mu}}{d \lambda} + \Gamma^{\mu}_{\kappa \nu} T^{\nu} \frac{dx^{\kappa}}{d \lambda} \ldotp\]

This is known as the geodesic equation. There is a factor of two that is a common gotcha when applying this equation. The symmetry of the Christoffel symbols \(\Gamma^{\mu}_{\kappa \nu} = \Gamma^{\mu}_{\nu \kappa}\) implies that when \(\kappa\) and \(\nu\) are distinct, the same term will appear twice in the summation.

If this differential equation is satisfied for one affine parameter \(\lambda\), then it is also satisfied for any other affine parameter \(\lambda' = a \lambda + b\), where a and b are constants (problem 5). Recall that affine parameters are only defined along geodesics, not along arbitrary curves.

We can’t start by defining an affine parameter and then use it to find geodesics using this equation, because we can’t define an affine parameter without first specifying a geodesic. Likewise, we can’t do the geodesic first and then the affine parameter, because if we already had a geodesic in hand, we wouldn’t need the differential equation in order to find a geodesic. The solution to this chicken-and-egg conundrum is to write down the differential equations and try to find a solution, without trying to specify either the affine parameter or the geodesic in advance. We will seldom have occasion to resort to this technique, an exception being example 19.

Uniqueness

The geodesic equation is useful in establishing one of the necessary theoretical foundations of relativity, which is the uniqueness of geodesics for a given set of initial conditions. This is related to axiom O1 of ordered geometry, that two points determine a line, and is necessary physically for the reasons discussed in section 1.5; briefly, if the geodesic were not uniquely determined, then particles would have no way of deciding how to move. The form of the geodesic equation guarantees uniqueness. To see this, consider the following algorithm for determining a numerical approximation to a geodesic:

1. Initialize \(\lambda\), the x^\(\mu\) and their derivatives \(\frac{dx^{\mu}}{d \lambda}\). Also, set a small step-size \(\Delta \lambda\) by which to increment \(\lambda\) at each step below.
2. For each i, calculate \(\frac{d^{2} x^{\mu}}{d \lambda^{2}}\) using the geodesic equation.
3. Add \((\frac{d^{2} x^{\mu}}{d \lambda^{2}}) \Delta \lambda\) to the currently stored value of \(\frac{dx^{\mu}}{d \lambda}\).
4. Add \((\frac{dx^{\mu}}{d \lambda}) \Delta \lambda\) to x^\(\mu\).
5. Add \(\Delta \lambda\) to \(\lambda\).
6. Repeat steps 2-5 until the geodesic has been extended to the desired affine distance.

Since the result of the calculation depends only on the inputs at step 1, we find that the geodesic is uniquely determined.

To see that this is really a valid way of proving uniqueness, it may be helpful to consider how the proof could have failed. Omitting some of the details of the tensors and the multidimensionality of the space, the form of the geodesic equation is essentially \(\ddot{x}\ + f \dot{x}^{2} = 0\), where dots indicate derivatives with respect to \(\lambda\). Suppose that it had instead had the form \(\ddot{x}^{2} + f \dot{x} = 0\). Then at step 2 we would have had to pick either a positive or a negative square root for \(\ddot{x}\). Although continuity would usually suffice to maintain a consistent sign from one iteration to the next, that would not work if we ever came to a point where \(\ddot{x}\) vanished momentarily. An equation of this form therefore would not have a unique solution for a given set of initial conditions.

The practical use of this algorithm to compute geodesics numerically is demonstrated in section 5.9.