5.5: Curvature Tensors

The example of the flea suggests that if we want to express curvature as a tensor, it should have even rank. Also, in a coordinate system in which the coordinates have units of distance (they are not angles, for instance, as in spherical coordinates), we expect that the units of curvature will always be inverse distance squared. Another way of putting this is that if we start with normal coordinates and then rescale all the coordinates by a factor of µ, a curvature tensor should scale down by \(\mu^{−2}\). (See section 5.11, for more on this topic.)

Combining these two facts, we find that a curvature tensor should have one of the forms R_ab R^a_bcd, . . . , i.e., the number of lower indices should be two greater than the number of upper indices. The following definition has this property, and is equivalent to the earlier definitions of the Gaussian curvature that were not written in tensor notation.

Definition of the Riemann curvature tensor: Let dp^c and dq^d be two infinitesimal vectors, and use them to form a quadrilateral that is a good approximation to a parallelogram.⁶ Parallel-transport vector v^b all the way around the parallelogram. When it comes back to its starting place, it has a new value v^b → v^b + dv^b. Then the Riemann curvature tensor is defined as the tensor that computes dv a according to dv^a = R^a_bcdv^bdp^cdq^d. (There is no standardization in the literature of the order of the indices.)

Note

Section 5.8 discusses the sense in which this approximation is good enough.

Example 7: A symmetry of the Riemann tensor

If vectors dp^c and dq^d lie along the same line, then dv^a must vanish, and interchanging \(dp^c\) and \(dq^d\) simply reverses the direction of the circuit around the quadrilateral, giving dv^a → − dv^a. This shows that R^a_bcd must be antisymmetric under interchange of the indices \(c\) and \(d\),

\[R^a_{bcd} = −R^a_{bdc}.\]

Figure \(\PageIndex{1}\) - The definition of the Riemann tensor. The vector v^b changes by dv^b when parallel-transported around the approximate parallelogram. (v^b is drawn on a scale that makes its length comparable to the infinitesimals dp^c, dq^d, and dv^b; in reality, its size would be greater than theirs by an infinite factor.)

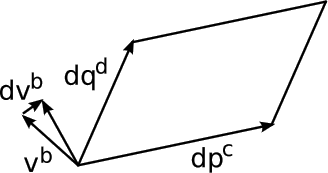
In local normal coordinates, the interpretation of the Riemann tensor becomes particularly transparent. The constant-coordinate lines are geodesics, so when the vector v^b is transported along them, it maintains a constant angle with respect to them. Any rotation of the vector after it is brought around the perimeter of the quadrilateral can therefore be attributed to something that happens at the vertices. In other words, it is simply a measure of the angular defect. We can therefore see that the Riemann tensor is really just a tensorial way of writing the Gaussian curvature

\[K = \frac{d \epsilon}{dA}.\]

In normal coordinates, the local geometry is nearly Cartesian, and when we take the product of two vectors in an antisymmetric manner, we are essentially measuring the area of the parallelogram they span, as in the three-dimensional vector cross product. We can therefore see that the Riemann tensor tells us something about the amount of curvature contained within the infinitesimal area spanned by dp^c and dq^d. A finite two-dimensional region can be broken down into infinitesimal elements of area, and the Riemann tensor integrated over them. The result is equal to the finite change \(\Delta\)v^b in a vector transported around the whole boundary of the region.

Example 8: Curvature tensors on a sphere

Let’s find the curvature tensors on a sphere of radius \(\rho\).

Construct normal coordinates (x, y) with origin O, and let vectors dp^c and dq^d represent infinitesimal displacements along x and y, forming a quadrilateral as described above. Then R^x_yxy represents the change in the x direction that occurs in a vector that is initially in the y direction. If the vector has unit magnitude, then R^x_yxy equals the angular deficit of the quadrilateral. Comparing with the definition of the Gaussian curvature, we find R^x_yxy = K = \(\frac{1}{\rho^{2}}\). Interchanging x and y, we find the same result for R y xyx . Thus although the Riemann tensor in two dimensions has sixteen components, only these two are nonzero, and they are equal to each other.

This result represents the defect in parallel transport around a closed loop per unit area. Suppose we parallel-transport a vector around an octant, as shown in Figure 5.4.2. The area of the octant is \((\frac{\pi}{2}) \rho^{2}\), and multiplying it by the Riemann tensor, we find that the defect in parallel transport is \(\frac{\pi}{2}\), i.e., a right angle, as is also evident from the figure.

The above treatment may be somewhat misleading in that it may lead you to believe that there is a single coordinate system in which the Riemann tensor is always constant. This is not the case, since the calculation of the Riemann tensor was only valid near the origin O of the normal coordinates. The character of these coordinates becomes quite complicated far from O; we end up with all our constant-x lines converging at north and south poles of the sphere, and all the constant-y lines at east and west poles.

Angular coordinates \((\phi, \theta)\) are more suitable as a large-scale description of the sphere. We can use the tensor transformation law to find the Riemann tensor in these coordinates. If O, the origin of the (x, y) coordinates, is at coordinates \((\phi, \theta)\), then \(\frac{dx}{d \phi} = \rho \sin \theta\) and \(\frac{dy}{d \theta} = \rho\). The result is \(R^{\phi}_{\theta \phi \theta} = R^{x}_{yxy} (\frac{dy}{d \theta})^{2} = 1\) and \(R^{\theta}_{\phi \theta \phi} = R^{y}_{xyx} (\frac{dx}{d \phi})^{2} = \sin^{2} \theta\). The variation in \(R^{\theta}_{\phi \theta \phi}\) is not due to any variation in the sphere’s intrinsic curvature; it represents the behavior of the coordinate system.

The Riemann tensor only measures curvature within a particular plane, the one defined by dp^c and dq^d, so it is a kind of sectional curvature. Since we’re currently working in two dimensions, however, there is only one plane, and no real distinction between sectional curvature and Ricci curvature, which is the average of the sectional curvature over all planes that include dq^d: R_cd = R^a_cad. The Ricci curvature in two spacelike dimensions, expressed in normal coordinates, is simply the diagonal matrix diag(K, K).