6.1: Event Horizons

One seemingly trivial way to generate solutions to the field equations in vacuum is simply to start with a flat Lorentzian spacetime and do a change of coordinates. This might seem pointless, since it would simply give a new description (and probably a less convenient and descriptive one) of the same old, boring, flat spacetime. It turns out, however, that some very interesting things can happen when we do this.

Figure \(\PageIndex{1}\): A Swiss commemorative coin shows the vacuum field equation.

The Event Horizon of an Accelerated Observer

Consider the uniformly accelerated observer described in example 4 and example 19. Recalling these earlier results, we have for the ship’s equation of motion in an inertial frame

\[x = \frac{1}{a} (\sqrt{1 + a^{2} t^{2}} - 1),\]

and for the metric in the ship’s frame

\[\begin{align} g'_{t' t'} &= (1 + ax')^{2} \\ g'_{x' x'} &= -1 \ldotp \end{align}\]

Since this metric was derived by a change of coordinates from a flat-space metric, and the Ricci curvature is an intrinsic property, we expect that this one also has zero Ricci curvature. This is straightforward to verify. The nonvanishing Christoffel symbols are

\[\Gamma^{t'}_{x' t'} = \frac{a}{1 + ax'} \]

and

\[\Gamma^{x'}_{t' t'} = a (1 + ax') \ldotp\]

The only elements of the Riemann tensor that look like they might be nonzero are \(R^{t'}_{t'x'x'}\) and \(R^{x'}_{t'x't'}\), but both of these in fact vanish.

Exercise \(\PageIndex{1}\)

Self-check: Verify these facts.

This seemingly routine exercise now leads us into some very interesting territory. Way back in section 1.1, we conjectured that not all events could be time-ordered: that is, that there might exists events in spacetime 1 and 2 such that 1 cannot cause 2, but neither can 2 cause 1. We now have enough mathematical tools at our disposal to see that this is indeed the case.

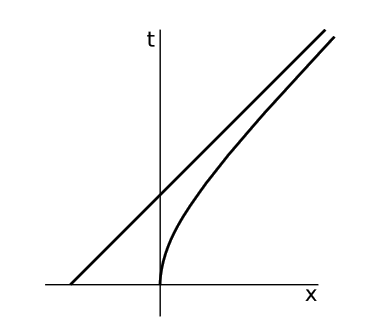
We observe that x(t) approaches the asymptote \(x = \frac{t−1}{a}\). This asymptote has a slope of 1, so it can be interpreted as the world-line of a photon that chases the ship but never quite catches up to it. Any event to the left of this line can never have a causal relationship with any event on the ship’s world-line. Spacetime, as seen by an observer on the ship, has been divided by a curtain into two causally disconnected parts. This boundary is called an event horizon. Its existence is relative to the world-line of a particular observer. An observer who is not accelerating along with the ship does consider an event horizon to exist. Although this particular example of the indefinitely accelerating spaceship has some physically implausible features (e.g., the ship would have to run out of fuel someday), event horizons are real things. In particular, we will see in section 6.3 that black holes have event horizons.

Interpreting everything in the (t', x') coordinates tied to the ship, the metric’s component g'_t't' vanishes at \(x' = − \frac{1}{a}\). An observer aboard the ship reasons as follows. If I start out with a head-start of \(\frac{1}{a}\) relative to some event, then the timelike part of the metric at that event vanishes. If the event marks the emission of a material particle, then there is no possible way for that particle’s world-line to have \(ds^2 > \)0. If I were to detect a particle emitted at that event, it would violate the laws of physics, since material particles must have \(ds^2 > 0\), so I conclude that I will never observe such a particle. Since all of this applies to any material particle, regardless of its mass m, it must also apply in the limit \(m → 0\), i.e., to photons and other massless particles. Therefore I can never receive a particle emitted from this event, and in fact it appears that there is no way for that event, or any other event behind the event horizon, to have any effect on me. In my frame of reference, it appears that light cones near the horizon are tipped over so far that their future light-cones lie entirely in the direction away from me.

Figure \(\PageIndex{2}\) - A spaceship (curved worldline) moves with an acceleration perceived as constant by its passengers. The photon (straight world-line) comes closer and closer to the ship, but will never quite catch up.

We’ve already seen in Example 14 that a naive Newtonian argument suggests the existence of black holes; if a body is sufficiently compact, light cannot escape from it. In a relativistic treatment, this should be described as an event horizon.

Information Paradox

The existence of event horizons in general relativity has deep implications, and in particular it helps to explain why it is so difficult to reconcile general relativity with quantum mechanics, despite nearly a century of valiant attempts. Quantum mechanics has a property called unitarity. Mathematically, this says that if the state of a quantum mechanical system is given, at a certain time, in the form of a vector, then its state at some point in the future can be predicted by applying a unitary matrix to that vector. A unitary matrix is the generalization to complex numbers of the ordinary concept of an orthogonal matrix, and essentially it just represents a change of basis, in which the basis vectors have unit length and are perpendicular to one another.

To see what this means physically, consider the following nonexamples. The matrix

\[\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\]

is not unitary, because its rows and columns are not orthogonal vectors with unit lengths. If this matrix represented the time-evolution of a quantum mechanical system, then its meaning would be that any particle in state number 1 would be left alone, but any particle in state 2 would disappear. Any information carried by particles in state 2 is lost forever and can never be retrieved. This also violates the time-reversal symmetry of quantum mechanics.

Another nonunitary matrix is:

\[\begin{pmatrix} 1 & 0 \\ 0 & \sqrt{2} \end{pmatrix}\]

Here, any particle in state 2 is increased in amplitude by a factor of \(\sqrt{2}\), meaning that it is doubled in probability. That is, the particle is cloned. This is the opposite problem compared to the one posed by the first matrix, and it is equally problematic in terms of timereversal symmetry and conservation of information. Actually, if we could clone a particle in this way, it would violate the Heisenberg uncertainty principle. We could make two copies of the particle, and then measure the position of one copy and the momentum of the other, each with unlimited precision. This would violate the uncertainty principle, so we believe that it cannot be done. This is known as the no-cloning theorem.¹

Note

Ahn et al. have shown that the no-cloning theorem is violated in the presence of closed timelike curves: arxiv.org/abs/1008.0221v1

The existence of event horizons in general relativity violates unitarity, because it allows information to be destroyed. If a particle is thrown behind an event horizon, it can never be retrieved.

Radiation from Event Horizons

In interesting twist on the situation was introduced by Bill Unruh in 1976. Observer \(B\) aboard the accelerating spaceship believes in the equivalence principle, so she knows that the local properties of space at the event horizon would seem entirely normal and Lorentzian to a local observer \(A\). (The same applies to a black hole’s horizon.) In particular, \(B\) knows that \(A\) would see pairs of virtual particles being spontaneously created and destroyed in the local vacuum. This is simply a manifestation of the time-energy form of the uncertainty principle, \(\Delta E \Delta t \le h\). Now suppose that a pair of particles is created, but one is created in front of the horizon and one behind it. To \(A\), these are virtual particles that will have to be annihilated within the time \(\Delta\)t, but according to \(B\) the one created in front of the horizon will eventually catch up with the spaceship, and can be observed there, although it will be red-shifted. The amount of redshift is given by

\[\sqrt{g'_{t' t'}} = \sqrt{(1+ax')^{2}}.\]

Say the pair is created right near the horizon, at \(x' = − \frac{1}{a}\). By the uncertainty principle, each of the two particles is spread out over a region of space of size \(\Delta x'\). Since these are photons, which travel at the speed of light, the uncertainty in position is essentially the same as the uncertainty in time. The forward-going photon’s redshift comes out to be a\(\Delta\)x' = a\(\Delta\)t', which by the uncertainty principle should be at least \(\frac{ha}{E}\), so that when the photon is observed by B, its energy is

\[E(\frac{ha}{E}) = ha.\]

Figure \(\PageIndex{3}\): Bill Unruh.

Now B sees a uniform background of photons, with energies of around ha, being emitted randomly from the horizon. They are being emitted from empty space, so it seems plausible to believe that they don’t encode any information at all; they are completely random. A surface emitting a completely random (i.e., maximum-entropy) hail of photons is a black-body radiator, so we expect that the photons will have a black-body spectrum, with its peak at an energy of about ha. This peak is related to the temperature of the black body by E ∼ kT, where k is Boltzmann’s constant. We conclude that the horizon acts like a black-body radiator with a temperature T ∼ \(\frac{ha}{k}\). The more careful treatment by Unruh shows that the exact relation is \(T = \frac{ha}{4 \pi^{2} k}\), or \(\frac{ha}{4 \pi^{2} kc}\) in SI units.

An important observation here is that not only do different observers disagree about the number of quanta that are present (which is true in the case of ordinary Doppler shifts), but about the number of quanta in the vacuum as well. B sees photons that according to A do not exist.

Let’s consider some real-world examples of large accelerations:

	acceleration (m/s^2)	temperature of horizon (K)
bullet fired from a gun	10^3	10^-17
electron in a CRT	10^7	10^-13
plasmas produced by intense laser pulses	10^21	10
proton in a helium nucleus	10^27	10^8

To detect Unruh radiation experimentally, we would ideally like to be able to accelerate a detector and let it detect the radiation. This is clearly impractical. The third line shows that it is possible to impart very large linear accelerations to subatomic particles, but then one can only hope to infer the effect of the Unruh radiation indirectly by its effect on the particles. As shown on the final line, examples of extremely large nonlinear accelerations are not hard to find, but the interpretation of Unruh radiation for nonlinear motion is unclear. A summary of the prospects for direct experimental detection of this effect is given by Rosu.² This type of experiment is clearly extremely difficult, but it is one of the few ways in which one could hope to get direct empirical insight, under controlled conditions, into the interface between gravity and quantum mechanics.

References

² http://xxx.lanl.gov/abs/gr-qc/9605032