General Theory of Relativity
- Page ID
- 3564
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Three "Easy" Pieces
Einstein used three different pieces to built the General Theory of Relativity, which we describe here.
Piece 1 - Geometry is Physics
Think of a wheel constructed of circular rods connected by spokes. The length of each rod, the circumference of the circle, is related to the radius r of the circle: the rods at larger radii are longer.
You may know that the length L of the rod is 2![]() times the radius.
times the radius.
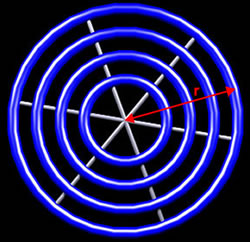
Here is a plot of how the length of the rod will vary with its radius. Think of a rod with a radius r and length L. Then another rod with a radius 2r will have a length of 2L.
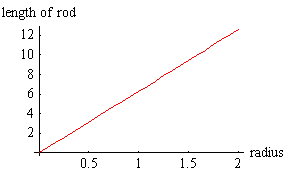
But what if the wheel is spinning at a high rate? We know from Special Relativity that rods that are moving relative to us have their lengths contracted along their direction of their motion. Thus the circular rods will have their length's contracted. The motion of the spokes of the wheel is perpendicular to their length, so we will conclude from Special Relativity that their lengths will not be contracted.
Thus, for the spinning wheel the length of the rod will depend on the radius according to the blue line, not the red one.
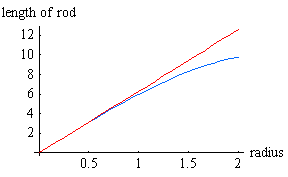
Here is a way to visualising the distortion of the lengths of the rods as the radius increases. For a given radius, the circumference is the distance around the upside-down "bowl" at a particular height. This is called an "embedding diagram."
Beware: this visualisation is not a graph of the shape of the spinning wheel: it just is a sometimes handy way of seeing how the circumference of the spinning wheel varies as the radius.
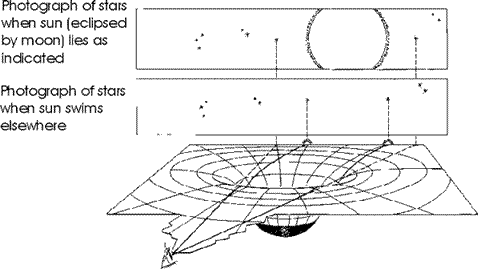
Now consider the figure to the right, which shows a distant star, the Sun, and the Earth. Clearly the figure is not drawn to scale.
There is a straight dotted line connecting the star and the Earth.
Imagine a light ray that leaves the star along the dotted line: it is headed directly for the Earth.
 However, we know that E = m c 2. And since the light that left the star has energy, we now know that it also has a mass. And all masses are attracted gravitationally by all other masses. So the light energy that left the star along the dotted line will be attracted gravitationally by the mass of the sun, which will cause its path to be deflected as shown. Thus that light ray from the star does not reach the Earth.
However, we know that E = m c 2. And since the light that left the star has energy, we now know that it also has a mass. And all masses are attracted gravitationally by all other masses. So the light energy that left the star along the dotted line will be attracted gravitationally by the mass of the sun, which will cause its path to be deflected as shown. Thus that light ray from the star does not reach the Earth.
In fact, it is the upper trajectory in the figure that represents the light from the Star that reaches the Earth.
The simple definition of a straight line is that it is the shortest distance between two points. And we also know that light rays are the fastest way of getting information from, say, the star to the Earth. Thus, the upper path in the figure defines a straight line.
We imagine a flat plane as representing all three spatial dimensions plus the time dimension, a Flatland analogy. Then, we are now led to the view that the effect of a mass such as the Sun is to curve spacetime, which we represent by another "embedding diagram."
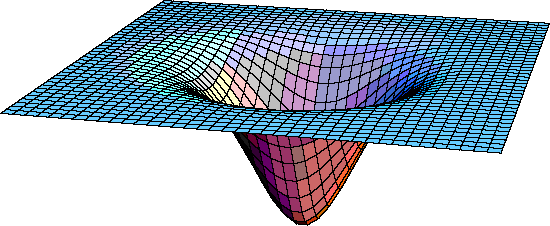
Embedding Diagram
We say that a flat spacetime has a Euclidean geometry. Then the effect of a mass is to make the geometry around itself non-Euclidean. And in a gravitational interaction everything is moving in "straight lines" in this curved spacetime. Technical note: sometimes one uses the word geodesic instead of saying "straight lines.'
Beware: the surface is a representation of the three spatial dimensions plus the time dimension. Thus there is no physical dimension into which the surface can be distorted. Thus, just as for the embedding diagram for the spinning wheel, the embedding diagram is just a visualisation technique.
"So long as one believes that the universe is a big machine, it is natural to think that its various parts can exert a force on one another. But the deeper science probes toward reality, the more clearly it appears that the universe it not like a machine at all. So Einstein's Law of Gravitation contains nothing about force. It describes the behavior of objects in a gravitational field - the planets, for example - not in terms of `attraction' but simply in terms of the paths they follow." -- Lincoln Barnett, The Universe and Dr. Einstein, pg. 42
This view also seems consistent with a much earlier statement of Chinese philosophy:
"The inviolability of natural laws rest on [the] principle of movement along the lines of least resistance. These laws are not forces external to things, but represent the harmony of movement immanent in them." -- I Ching
It is also reminiscent of a graffiti: Gravity is a myth; the Earth sucks!
"Spacetime tells mass how to move; mass tells spacetime how to curve." -- Edwin F. Taylor and John Archibald Wheeler, Exploring Black Holes, back cover. This well known quote from Taylor and Wheeler also appears in many other places.
Further discussion of Euclidean and non-Euclidean geometries may be found here.
Piece 2 - Hiding the Universe in the Universe
Consider two bodies that have electric charge Q and q. We know that because they carry electric charge, they exert forces on each other. We call the force electrostatic.

Now we consider two bodies that have masses M and m. Because they both have mass, in the Newtonian description we say that they exert forces on each other. We call the force gravitation.

Now we consider two bodies with masses M and m that are both moving to the right at the same speed relative to us. They both have inertia. Since they are traveling at the same speed, the body with the larger mass will have a larger inertia.
Above we have used the word mass in two different ways.
- We refer to the property of objects that causes them to interact gravitationally with other objects with this property. The magnitude of the gravitational interaction is proportional to the amount of gravitational mass the objects have.
- We refer to the property of objects that gives them inertia. The inertia of an object is the amount of its inertial mass times the speed it is moving relative to use. Thus a very massive ship moving at a small speed has considerable inertia, as does a light object moving at a high speed.
Note that although we use the word mass in both cases, there is no immediate and obvious reason why this inertial mass and gravitational mass should be related to each other.
We can compare the gravitational mass of two objects by weighing them, i.e. measuring their gravitational interaction with the Earth. We can also compare the inertial mass of same two objects by measuring their effects in collisions with other objects. These experiments have been done to great accuracy and precision, and the comparisons always come out the same. Thus we conclude that the gravitational and inertial mass are experimentally found to be the same for all objects.
This is different from comparing, say, the inertial mass of two objects with their electric charges. There is no relation between the two, and we can have an object with a large inertial mass but no electric charge and another object with the same inertial mass and a non-zero electric charge.
Einstein was the father of the theories of relativity, but Ernst Mach was the grandfather. Mach elevated and explained the equality of gravitational and inertial mass into what is now called Mach's Principle. As we shall see, although we will be able to achieve some understanding of this principle, a complete and unambiguous statement of it is difficult, maybe even impossible.
One approach involves the Foucault Pendulum, which was invented by Jean Bernard Foucault (pronounced foo-ko) in 1851 in Paris and was demonstrated for the first time at the world's fair in the Pantheon in Paris.

Foucault Pendulum at the University of Louisville
The pendulum, the big brass ball in the above figure, swings back and forth, but the plane of the oscillation rotates, making a complete revolution every 24 hours. The reason is that the Earth is rotating on its axis. From our perspective, it seems the entire universe circles us every 24 hours. However, the pendulum seems to show that it is the Earth that is rotating, not the universe
The principle of inertia says that every body will continue at rest or in uniform motion in a straight line unless forced to change that state of motion. And the Foucault pendulum is trying to obey that principle by rotating its plane of oscillation as the Earth turns under it. So this is a consequence of the inertial mass of the ball of the pendulum.
Here is what Mach said about the Foucault pendulum:
"The universe is not twice given, with an earth at rest and an earth in motion; but only once, with its relative motions alone determinable. It is accordingly, not permitted us to say how things would be if the earth did not rotate." -- The Science of Mechanics, T.J. McCormack, trans., pg. 266.
What he is suggesting is essentially that the property of inertia of the Foucault pendulum here is related to its gravitational interaction with the mass of the universe there.
Jay Orear stated the viewpoint of Mach's Principle nicely:
"The point of view taken here is that your head is the center of the universe and is always at rest. Whenever you bump your head against a wall, the distant galaxies have suddenly accelerated and exert a strong gravitational force on your head. In order to keep your heat 'at rest', the wall must exert an equal and opposite contact force. So the next time you bump your head or stub your toe, you can blame it on the distant galaxies." -- Fundamental Physics 2nd ed., pg. 288.
It is tempting to state Mach's Principle as follows:
In a universe with only one test mass, that mass would not obey the Principle of Inertia. At one moment it could be at rest, at the next moment it could abruptly be in motion.
The problem with this form is that it violates the basis of Mach's Principle, that the universe is only once given. Thus we can only talk about the universe we have, not some hypothetical non-existent one. It is probably this feature that makes a concise statement of the principle so difficult.
Here is another attempt to state the principle:
"Einstein gave the name Mach's Principle to the following related ideas:
- that only relative motion is observable and hence that there should be no dynamically privileged reference frames;
- that inertial forces should arise from a gravitational interaction between matter only, and so from an observer-dependent splitting of the total gravitational field;
- that spacetime is not an absolute element of physics but that its [geometry] is totally dependent on the matter content of the universe."
Reference: D.J. Raine, Monthly Notices, Roy. Astron. Soc. 171, (1975) pg. 507.
The small Flash animation of the Foucault pendulum is available here; it will appear in a separate window.
Incidentally, the title of this sub-section is from Chuang Tsu 6.
Piece 3 - The Equivalence Principle
Imagine that the room in which you are sitting is a cabin on a rocket ship. The cabin has no portholes so you can not look out. Devise an experiment to determine which of the following two situations are true:
- The rocket ship is sitting stationary on the surface of the Earth, where the acceleration due to gravity is 9.8 meters per second per second down.
- The rocket ship is in free space accelerating upward at 9.8 meters per second per second.
It turns out that for a reasonably small cabin on the rocket ship, no such experiment can be devised. Einstein elevated this to a general principle: "We shall therefore assume complete physical equivalence between the gravitational field and the corresponding acceleration of the reference system. (Reference: Jahrbuch der Radioaktivitat un Elektronik 4 (1908) pg. 443.) We call this Einstein's Equivalence Principle, which he later described as "the happiest thought of my life."
Einstein once stated the principle as:
"For an observer in free fall off the roof of his house, there exists for him during his fall no gravity."
At the very beginning of this document I stated that building a theory that considers observers in any state of relative motion, including relative acceleration, would also turn out to be a theory of gravitation. The Equivalence Principle is why this is true. A few years ago a student wrote a paper which had an appropriate typo: gravitivity.
There is a small subtlety about the Equivalence Principle, which is discussed here.
Einstein's Synthesis
The following figure neatly summarises Einstein's achievement.
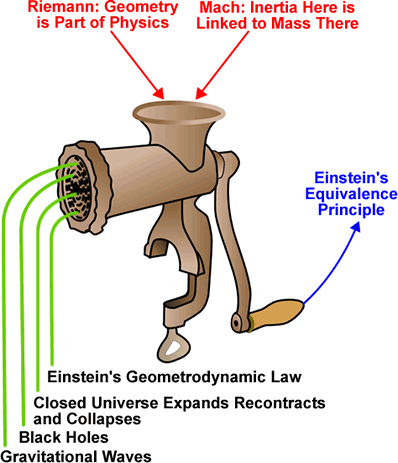
Based one a figure by J.A. Wheeler, "From Relativity to Mutability" in J. Mehra, ed., The Physicist's Conception of Nature (Reidel, 1973), pg. 205.
Some chronology may be interesting here. Einstein published the Special Theory of Relativity in 1905, based on 10 years of struggle with the question of what he would see if he pursued a beam of light at the speed of light. He thought of the Equivalence Principle a couple of years later, publishing it in 1908. He did not complete and publish the General Theory of Relativity until 1915, although he had been working hard on the problem since 1908. As he wrote to Sommerfeld in 1912:
"I am exclusively occupied with the problem of gravitation and hope with the help of a local mathematician friend [Marcel Grossman] to overcome all the difficulties. One thing is certain, however, that never in life have I been quite so tormented. A great respect for mathematics has been instilled within me, the subtler aspects of which, in my stupidity, I regarded until now as pure luxury."
The theory makes a number of predictions, which we will discuss.
Stellar Aberration
According to the theory, the apparent position of the stars is shifted when the light from them passes near the Sun and is deflected. This phenomenon is essentially how we began this discussion of the General Theory of Relativity. It has been experimentally confirmed many times.
One of the first such confirmations, and Einstein's attitudes towards his theory, is provided in the following account by Ilse Rosenthal-Schneider:
"Einstein was discussing some problems with me in his study when he suddenly interrupted his explanation and handed me a cable from the windowsill with the words, `This may interest you.' It was the news from Eddington confirming the deviation of light rays near the sun that had been observed during the eclipse. I exclaimed enthusiastically, `How wonderful, this is almost what you calculated.' He was quite unperturbed.` I knew that the theory was correct. Did you doubt it?' When I said, `Of course not, but what would you have said if there had not been such a confirmation?' He retorted, `Then I would have to be sorry for dear God. The theory is correct'."
Reference: H. Woolf, ed., Some Strangeness in the Proportion (Addison-Wesley, 1980), pg. 523.
A small detail
It turns out that the phenomenon of stellar aberration is also predicted by Newtonian concepts if, like him, we assume that light is made of particles whose speed is c relative to the ether. The experimental existence of the effect was first observed by James Bradley in 1727. However the magnitude of the effect predicted by the Newtonian analysis differs from the magnitude predicted by General Relativity by a factor of 2. The difference can be attributed to the fact that the Newtonian view is one dimension short: the idea of spacetime consisting of four dimensions is missing. The experimental data confirms that the General Relativity prediction is correct and the Newtonian one is not.
Expanding Universe
In 1915, when Einstein was finishing up his General Theory he realised that it predicted an expanding universe. However, the permanence of the universe was a fixed item of Western philosophy. This conflict between a dynamic non-permanent universe and the firm philosophical beliefs of the day bothered Einstein greatly. In fact, he weakened and modified his theory, introducing a cosmological constant, a fudge factor to make the universe static.
In 1929 Edwin Hubble was doing some interesting observational astronomy. It was known that there is a class of stars called Cepheid variables whose intensity varies periodically. Further there was a known relationship between the absolute brightness of a Cepheid variable star and the rate of the oscillation of its intensity. Thus by measuring the brightness of such a star on Earth we can calculate how far away the star is.
In addition, the spectrum of the light from a star when the star is at rest relative to us was also known. However, if the star is, say, moving away from us the Doppler effect will cause the wavelengths of the light to be shifted towards the red. You have probably noticed the Doppler effect when a car playing loud music goes by you: as it approaches the sound is shifted towards shorter wavelengths and as it recedes the sound is shifted towards longer wavelengths.
So by measuring the shift in the spectrum of light from a Cepheid variable we can determine its speed relative to us.
When Hubble did these measurements he discovered that the stars are moving away from us, and the further away they are the faster they are receding from us. The figure to the right shows a more modern set of data.
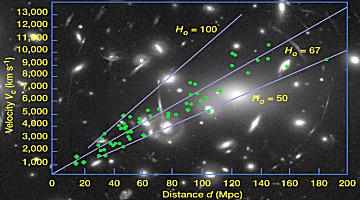
Source:
Here is a model that explains how such data can arise. We imagine that we are making raisin bread, but have misread the recipe and instead of putting in one teaspoon of baking powder we have put in one pound! As the dough starts to rise, it begins to fill our kitchen. If we stand on any given raisin, all the other raisins will be receding away from us; the further away the raisin is the faster it recedes away from us. Similarly, if the universe is expanding and the raisins represent the stars we will get the result observed by Hubble.
Here is a more accurate model. We imagine the universe as a Flatland confined to the surface of a balloon. Paint some dots on the balloon and think of them as the stars. Begin blowing up the balloon. If you stand on any dot and measure the position and speed of any other dot you will find that all the dots are receding away from you and their speed away from you increases the further away the dot is. Note that the dots are not moving on the surface of the balloon, rather the fabric of the balloon itself is expanding. Also remember that you must make your distance measurements staying within the surface of the balloon; the higher-dimensional direct connection from point to point via a chord inside the balloon is not accessible to us.
When Hubble published his results, Einstein immediately dropped the cosmological constant, calling it "the biggest mistake of my life."
Note that the Hubble data, as well as the two models we have used to think about it, indicate that at some time in the past the universe was very very small. In fact, current cosmology tends to favor a view that at some time on the order of 15 billion years ago the size of the universe was zero. At this time, the temperature was infinite, and the Big Bang occurred, initiating this cycle of the universe.
Further information on cosmology may be found here; total file size including graphics is about 70k.
Gravitational Time Dilation
Just as moving clocks run slow, General Relativity predicts that clocks in gravitational fields run slow. This prediction of the theory has been confirmed many times. A small document that does a non-mathematical derivation of this prediction of the theory has been prepared; the html version is here and the pdf version is here.
One of the prettiest tests of this prediction was performed by Hafele and Keating in 1971. They flew cesium beam atomic clocks around the world on regularly scheduled commercial airline flights. One clock remained in their laboratory outside Washington DC, one was flown to the East, and the other to the West. There are two effects at work:
- Special Relativity predicts that moving clocks run slowly.
- General Relativity predicts that clocks in gravitational fields run slowly. The clock in the laboratory is in a stronger field, a region with more curvature, than clocks on the airplanes.
They analysed the flight data to calculate the predicted effects and when all the clocks were back in the lab compared the measured elapsed times. Here are the predicted and measured elapsed time relative to the clock that stayed in the lab. All times are in non-seconds.
| Eastbound clock | Westbound clock | |
|---|---|---|
| Special Relativity prediction | lose 184 ± 18 | gain 96 ± 10 |
| General Relativity prediction | gain 144 ± 14 | gain 179 ± 18 |
| Total predicted effect | lose 40 ± 23 | gain 275 ± 21 |
| Measured | lost 59 ± 10 | gained 273 ± 21 |
The predicted effect matched the measured one within experimental uncertainties.
Question: why does the Eastbound clock lose time while the Westbound clock gains time?
An Application - Global Positioning Systems
As you may know, there are over two dozen GPS satellites in orbit around the Earth. Each satellite has an extremely accurate atomic clock, and broadcasts the time as measured by its own clock. The GPS receiver receives the signals from the satellites, and by measuring the time delay between when the signal was sent and when it was received calculates where it is.
However, as with the Hafele and Keating experiment, the clock on the GPS satellite is subject to time dilations due to its motion and its altitude. If these corrections are not taken into account, the position measured by the receiver will drift by up to 11 km for every day that the satellite has been in orbit.
Reference: Neil Ashby,"Relativity and the Global Positioning System," Physics Today, May 2002.
Gravitational Length Contraction
Lengths of objects in gravitational fields are contracted according to the theory. The prediction has never been tested. For the keen, you may wish to derive this prediction using the same techniques used in the previous sub-section to derive gravitational time dilation.
Gravity Waves
Just as an oscillating electric charge generates an electromagnetic wave, General Relativity predicts that an oscillating mass will generate a gravity wave. Many attempts have been made to detect the existence of gravity waves, with results that are ambiguous at best.
There are currently some experiments that are being designed to attempt to detect these waves. One large project is the Laser Interferometer Gravitational-Wave Observatory (LIGO). The home page of the project is http://www.ligo.caltech.edu/.
Advance of the Perihelion
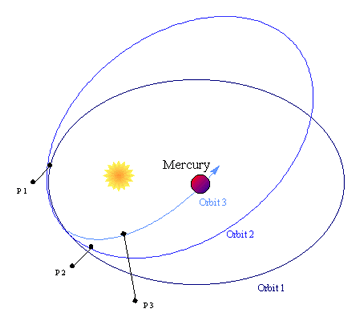 According to classical Newtonian mechanics, the planets move in elliptical orbits around the Sun. These orbits, in the absence of perturbations from other planets, comets, etc., should exactly repeat themselves.
According to classical Newtonian mechanics, the planets move in elliptical orbits around the Sun. These orbits, in the absence of perturbations from other planets, comets, etc., should exactly repeat themselves.
In General Relativity these ellipses do not exactly repeat. The point of closest approach of a planet to the sun is called the perihelion, which has the same root as periscope.
The figure shows this "advance of the perihelion" predicted by General Relativity, although the advance is not nearly as large as the figure indicates. (Source: astrosun.tn.cornell.edu/cours...1/merc_adv.htm )
A small Flash animation of this phenomenon is available here; it will appear in a separate window.
This prediction of General Relativity has been experimentally tested for the orbit or Mercury. The measurements are difficult but it is probably fair to say the prediction is confirmed.
Black Holes
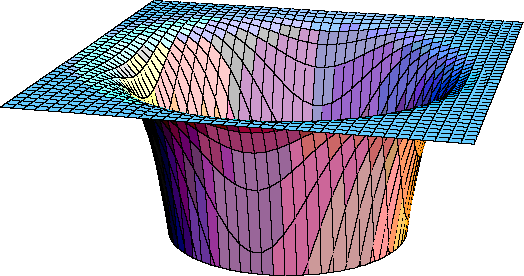
When a gravitational field, a curvature in spacetime, becomes sufficiently intense, the theory predicts that the matter causing the field can be literally crushed out of existence. The curvature becomes so intense that a hole is punched in the fabric of spacetime. This phenomenon is called a black hole.
There are many observations that strongly suggest the existence of black holes that were formed when a star exhausted its nuclear fuel.
A more complete discussion of black holes has been prepared. The html version is here and the pdf version is here.
Embedding Diagram of a Black Hole
The Units of Mass
This section is somewhat more mathematical than is typical in this document.
In Special Relativity, the mathematical description often involves equations which include the speed of light c. For example, the formula for time dilation is:
![]()
Eventually we tire of writing all those c's in all those equations and seek a simpler way. In our discussion of Special Relativity we found such a simplification: quit measuring time in sacred units of seconds, start measuring it in "everyday" units of meters. In these natural units c = 1 and never needs to be written down. The speed of light neatly does the conversion of units:
time in meters = c in meters per second x time in seconds
I leave it to you to ponder whether this choice of units is just a mathematical convenience or tells us something more profound about the world.
When describing gravity mathematically the universal gravitational constant G constantly appears. For example, in the Newtonian description the force F a mass M exerts on a mass m a distance r away is:
![]()
In General Relativity, if we measure spatial distance in, say, meters, time in seconds, and masses in kilograms, the factor G/c2 appears over and over again. For example, the Schwarzschild metric is:
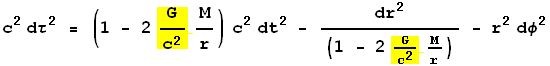
The value of G/c2 is a very small number whose units are meters/kilogram. This suggests that we can avoid writing down that factor over and over again by measuring mass in units of distance: meters! We can convert the units with:
![]()
So, if we measure masses as well as distances and times in units of meters we never need to write either c or G/c2 in our equations: they are both exactly equal to one.
Measuring both time and mass in meters, the Schwarzschild metric becomes somewhat simpler to write:
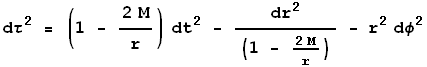
Here are some values of the masses in everyday units of kilograms and in "geometrical units":
| Mass in kilograms | Mass in "geometrical units" | Radius | |
|---|---|---|---|
| Earth | 6.0 x 1024 | 0.4 cm | 6371 km |
| Sun | 2.0 x 1030 | 1.5 km | 700,000 km |
| Black hole at center of our galaxy | 5.2 x 1036 | 3,800,000 km | 7,600,000 km |
For the black hole in the above table, the "radius" is the Schwarzschild radius. For the math-philic, can you see from the Schwarzschild metric above why it is exactly twice the mass as measured in geometrical units?
Systems of Units
One of the many surprises we learn from classical physics is that every physical quantity can be specified in terms of exactly four "fundamental" units:
- A length, e.g. meters
- A time, e.g. seconds
- A mass, e.g. kilograms
- An electric charge
Every other quantity is expressed as combinations of four or less of these units.
In Relativity we seem to have collapsed the list to from four to two fundamental units: length and electric charge. True happiness would be collapsing it to a single unit, length for example.
A Favorite Puzzle
A bucket of water has a spring soldered to the bottom, as shown. A cork is attached the spring, and is therefore suspended under the surface of the water.
You are on top of the CN tower, holding the bucket, and step off. While falling towards the ground, do you see the cork move towards the top of the water, towards the bottom of the bucket, or stay where it is relative to the bucket and the water?

