2.9: Equilibrium and Stability
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.09:_Equilibrium_and_Stability), /content/body/p/span, line 1, column 23
Equilibrium
Suppose we have two systems, A and B, which are free to exchange energy, volume, and particle number, subject to overall conservation rules
EA+EB=E,VA+VB=V,NA+NB=N ,
where E, V, and N are fixed. Now let us compute the change in the total entropy of the combined systems when they are allowed to exchange energy, volume, or particle number. We assume that the entropy is additive,
dS=[(∂SA∂EA)∗VA,NA−(∂SB∂EB)∗VB,NB]dEA+[(∂SA∂VA)∗EA,NA−(∂SB∂VB)∗EB,NB]dVA+[(∂SA∂NA)∗EA,VA−(∂SB∂NB)∗EB,VB]dNA .
Note that we have used dEB=−dEA, dVB=−dVA, and dNB=−dNA. Now we know from the Second Law that spontaneous processes result in TdS>0, which means that S tends to a maximum. If S is a maximum, it must be that the coefficients of dEA, dVA, and dNA all vanish, else we could increase the total entropy of the system by a judicious choice of these three differentials. From TdS=dE+pdV−μ,dN, we have
1T=(∂S∂E)∗V,N,pT=(∂S∂V)∗E,N,μT=−(∂S∂N)∗E,V .
Thus, we conclude that in order for the system to be in equilibrium, so that S is maximized and can increase no further under spontaneous processes, we must have
TA=TB(thermal equilibrium)pATA=pBTB(mechanical equilibrium)μATA=μBTB(chemical equilibrium)
Stability
Next, consider a uniform system with energy E′=2E, volume V′=2V, and particle number N′=2N. We wish to check that this system is not unstable with respect to spontaneously becoming inhomogeneous. To that end, we imagine dividing the system in half. Each half would have energy E, volume V, and particle number N. But suppose we divided up these quantities differently, so that the left half had slightly different energy, volume, and particle number than the right, as depicted in Figure 2.9.1 . Does the entropy increase or decrease? We have
ΔS=S(E+ΔE,V+ΔV,N+ΔN)+S(E−ΔE,V−ΔV,N−ΔN)−S(2E,2V,2N)=∂2S∂E2(ΔE)2+∂2S∂V2(ΔV)2+∂2S∂N2(ΔN)2+2∂2S∂E∂VΔEΔV+2∂2S∂E∂NΔEΔN+2∂2S∂V∂NΔVΔN .
Thus, we can write
ΔS=∑i,jQ∗ijΨ∗iΨ∗j ,
where
Q=(∂2S∂E2∂2S∂E∂V∂2S∂E∂N∂2S∂E∂V∂2S∂V2∂2S∂V∂N∂2S∂E∂N∂2S∂V∂N∂2S∂N2)
is the matrix of second derivatives, known in mathematical parlance as the Hessian, and Ψ=(ΔE,ΔV,ΔN). Note that Q is a symmetric matrix.
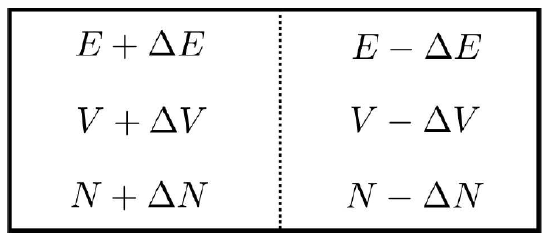
Since S must be a maximum in order for the system to be in equilibrium, we are tempted to conclude that the homogeneous system is stable if and only if all three eigenvalues of Q are negative. If one or more of the eigenvalues is positive, then it is possible to choose a set of variations Ψ such that ΔS>0, which would contradict the assumption that the homogeneous state is one of maximum entropy. A matrix with this restriction is said to be negative definite. While it is true that Q can have no positive eigenvalues, it is clear from homogeneity of S(E,V,N) that one of the three eigenvalues must be zero, corresponding to the eigenvector Ψ=(E,V,N). Homogeneity means S(λE,λV,λN)=λS(E,V,N). Now let us take λ=1+η, where η is infinitesimal. Then ΔE=ηE, ΔV=ηV, and ΔN=ηN, and homogeneity says S(E±ΔE,V±ΔV,N±ΔN)=(1±η)S(E,V,N) and ΔS=(1+η)S+(1−η)S−2S=0. We then have a slightly weaker characterization of Q as negative semidefinite.
However, if we fix one of the components of (ΔE,ΔV,ΔN) to be zero, then Ψ must have some component orthogonal to the zero eigenvector, in which case ΔS<0. Suppose we set ΔN=0 and we just examine the stability with respect to inhomogeneities in energy and volume. We then restrict our attention to the upper left 2×2 submatrix of Q. A general symmetric 2×2 matrix may be written
Q=(abbc)
It is easy to solve for the eigenvalues of Q. One finds
λ∗±=(a+c2)±√(a−c2)2+b2 .
In order for Q to be negative definite, we require λ∗+<0 and λ∗−<0. Thus, TrQ=a+c=λ∗++λ∗−<0 and detQ=ac−b2=λ∗+λ∗−>0. Taken together, these conditions require
a<0,c<0,ac>b2 .
Going back to thermodynamic variables, this requires
∂2S∂E2<0,∂2S∂V2<0,∂2S∂E2⋅∂2S∂V2>(∂2S∂E∂V)2 .
Thus the entropy is a concave function of E and V at fixed N. Had we set ΔE=0 and considered the lower right 2×2 submatrix of Q, we’d have concluded that S(V,N) is concave at fixed E. Since (∂S∂E)∗V=T−1, we have ∂2S∂E2=−1T2(∂T∂E)∗V=−C∗VT2<0 and we conclude C∗V>0 for stability.
Many thermodynamic systems are held at fixed (T,p,N), which suggests we examine the stability criteria for G(T,p,N). Suppose our system is in equilibrium with a reservoir at temperature T∗0 and pressure p∗0. Then, suppressing N (which is assumed constant), we have
G(T∗0,p∗0)=E−T∗0S+p∗0V .
Now suppose there is a fluctuation in the entropy and the volume of our system, which is held at fixed particle number. Going to second order in ΔS and ΔV, we have
ΔG=[(∂E∂S)∗V−T∗0]ΔS+[(∂E∂V)∗S+p∗0]ΔV+12[∂2E∂S2(ΔS)2+2∂2E∂S∂VΔSΔV+∂2E∂V2(ΔV)2]+… .
Equilibrium requires that the coefficients of ΔS and ΔV both vanish, that T=(∂E∂S)∗V,N=T∗0 and p=−(∂E∂V)∗S,N=p∗0 . The condition for stability is that ΔG>0 for all (ΔS,ΔV). Stability therefore requires that the Hessian matrix Q be positive definite, with
Q=(∂2E∂S2∂2E∂S∂V∂2E∂S∂V∂2E∂V2) .
Thus, we have the following three conditions:
∂2E∂S2=(∂T∂S)∗V=TC∗V>0∂2E∂V2=−(∂p∂V)∗S=1Vκ∗S>0N∑N∂2E∂S2⋅∂2E∂V2−(∂2E∂S∂V)2=TVκ∗SC∗V−(∂T∂V)2S>0 .
As we shall discuss below, the quantity α∗S≡1V(∂V∂T)∗S,N is the adiabatic thermal expansivity coefficient. We therefore conclude that stability of any thermodynamic system requires
C∗VT>0,κ∗S>0,α∗S>√κ∗SC∗VVT.


