4.1: Microcanonical Ensemble (μCE)
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.01:_Microcanonical_Ensemble_(CE)), /content/body/p/span, line 1, column 23
The microcanonical distribution function
We have seen how in an ergodic dynamical system, time averages can be replaced by phase space averages:
ergodicity⟺⟨f(φ)⟩∗t=⟨f(φ)⟩∗S ,
where
⟨f(φ)⟩∗t=lim
and
\big\langle f(\Bvphi)\big\rangle\ns_S=\int\!\!d\mu\,f(\Bvphi)\,\delta\big(E-\HH(\Bvphi)\big) \bigg/ \!\int\!\!d\mu\,\delta\big(E-\HH(\Bvphi)\big) \ .
Here \HH(\Bvphi)=\HH(\Bq,\Bp) is the Hamiltonian, and where \delta(x) is the Dirac \delta-function1. Thus, averages are taken over a constant energy hypersurface which is a subset of the entire phase space.
We’ve also seen how any phase space distribution \vrh(\Lambda\ns_1,\ldots,\Lambda\ns_k) which is a function of conserved quantitied \Lambda\ns_a(\Bvphi) is automatically a stationary (time-independent) solution to Liouville’s equation. Note that the microcanonical distribution,
\vrh\nd_E(\Bvphi)=\delta\big(E-\HH(\Bvphi)\big) \bigg/\! \!\int\!\!d\mu\,\delta\big(E-\HH(\Bvphi)\big)\ ,
is of this form, since \HH(\Bvphi) is conserved by the dynamics. Linear and angular momentum conservation generally are broken by elastic scattering off the walls of the sample.
So averages in the microcanonical ensemble are computed by evaluating the ratio
\big\langle A\big\rangle = {\Tra A\,\delta(E-\HH)\over \Tra\delta(E-\HH)}\ ,
where \Tra means ‘trace’, which entails an integration over all phase space:
\Tra A(q,p)\equiv {1\over N!}\prod_{i=1}^N\int\!{d^d\!p\ns_i\,d^d\!q\ns_i\over (2\pi\hbar)^d}\,A(q,p)\ . \label{trcl}
Here N is the total number of particles and d is the dimension of physical space in which each particle moves. The factor of 1/N!, which cancels in the ratio between numerator and denominator, is present for indistinguishable particles2. The normalization factor (2\pi\hbar)^{-Nd} renders the trace dimensionless. Again, this cancels between numerator and denominator. These factors may then seem arbitrary in the definition of the trace, but we’ll see how they in fact are required from quantum mechanical considerations. So we now adopt the following metric for classical phase space integration:
d\mu={1\over N!}\,\prod_{i=1}^N {d^d\!p\ns_i\,d^d\!q\ns_i\over (2\pi\hbar)^d}\ .
Density of States
The denominator,
D(E)=\Tra \delta(E-\HH)\ ,
is called the density of states. It has dimensions of inverse energy, such that
\begin{align} D(E)\,\RDelta E &=\int\limits_E^{E+\RDelta E}\hskip-0.4cm dE'\!\int\!\!d\mu\>\delta(E'-\HH)=\hskip-0.8cm \int\limits_{E<\HH<E+\RDelta E}\hskip-0.8cm d\mu\label{DOSeqn}\\ &= \hbox{\# of states with energies between $E$ and $E+\RDelta E$}\ .\nonumber\end{align}
Let us now compute D(E) for the nonrelativistic ideal gas. The Hamiltonian is
\HH(q,p)=\sum_{i=1}^N {\Bp_i^2\over 2m}\ .
We assume that the gas is enclosed in a region of volume V, and we’ll do a purely classical calculation, neglecting discreteness of its quantum spectrum. We must compute
D(E)={1\over N!}\int\!\prod_{i=1}^N {d^d\!p\ns_i\,d^d\!q\ns_i\over (2\pi\hbar)^d}\>\delta\bigg(\!E-\sum_{i=1}^N {\Bp_i^2\over 2m}\bigg)\ .
We shall calculate D(E) in two ways. The first method utilizes the Laplace transform, Z(\beta):
Z(\beta)=\CL\big[D(E)\big]\equiv\int\limits_0^\infty\!\!dE\>e^{-\beta E}\,D(E) = \Tra e^{-\beta \HH}\ . \label{Zlap}
The inverse Laplace transform is then
D(E)=\CL^{-1}\big[Z(\beta)\big]\equiv\!\!\int\limits_{c-i\infty}^{c+i\infty}\!\!\!{d\beta\over 2\pi i}\>e^{\beta E}\,Z(\beta)\ ,
where c is such that the integration contour is to the right of any singularities of Z(\beta) in the complex \beta-plane. We then have
\begin{split} Z(\beta)&={1\over N!}\prod_{i=1}^N\int\!{d^d\!x\ns_i\, d^d\!p\ns_i\over (2\pi\hbar)^d}\>e^{-\beta\Bp_i^2/2m}\\ &={V^N\over N!}\left(\int\limits_{-\infty}^\infty\!\!{dp\over 2\pi\hbar}\>e^{-\beta p^2/2m}\right)^{\!\!Nd}\\ &={V^N\over N!}\bigg({m\over 2\pi\hbar^2}\bigg)^{\!\!Nd/2}\,\beta^{-Nd/2}\ . \label{zideal} \end{split}
The inverse Laplace transform is then
\begin{split} D(E)&={V^N\over N!} \bigg({m\over 2\pi\hbar^2}\bigg)^{\!\!Nd/2}\oint\limits_\CC\!\!{d\beta\over 2\pi i}\>e^{\beta E}\,\beta^{-Nd/2}\\ &={V^N\over N!}\,\bigg({m\over 2\pi\hbar^2}\bigg)^{\!\!Nd/2}\,{E\nsub^{{1\over 2}Nd-1}\over \RGamma(Nd/2)}\ , \end{split}
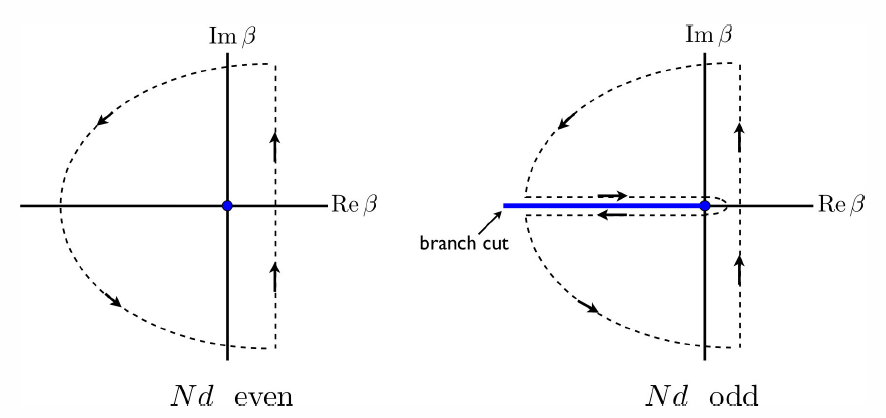
exactly as before. The integration contour for the inverse Laplace transform is extended in an infinite semicircle in the left half \beta-plane. When Nd is even, the function \beta^{-Nd/2} has a simple pole of order Nd/2 at the origin. When Nd is odd, there is a branch cut extending along the negative {Re}\,\beta axis, and the integration contour must avoid the cut, as shown in Figure \PageIndex{1}. One can check that this results in the same expression above, we may analytically continue from even values of Nd to all positive values of Nd.
For a general system, the Laplace transform, Z(\beta)=\CL\big[D(E)\big] also is called the partition function. We shall again meet up with Z(\beta) when we discuss the ordinary canonical ensemble.
Our final result, then, is
D(E,V,N)={V^N\over N!}\,\bigg({m\over 2\pi\hbar^2}\bigg)^{\!\!Nd/2}\,{E\nsub^{{1\over 2}Nd-1}\over \RGamma(Nd/2)}\ .
Here we have emphasized that the density of states is a function of E, V, and N. Using Stirling’s approximation,
\ln N! = N\ln N - N + \half \ln N + \half \ln(2\pi) + \CO\big(N^{-1}\big)\ ,
we may define the statistical entropy,
S(E,V,N)\equiv \kB\ln D(E,V,N) = N\kB \,\phi\bigg({E\over N}\, , \,{V\over N}\bigg) + \CO(\ln N)\ , \label{statent}
where
\phi\bigg({E\over N}\, , \,{V\over N}\bigg)={d\over 2}\,\ln\!\bigg({E\over N}\bigg) + \ln\! \bigg({V\over N} \bigg) +{d\over 2}\,\ln\!\bigg({m\over d\pi\hbar^2}\bigg)+\big( 1+\half d\big)\ . \label{phinrel}
Recall \kB=1.3806503\times 10^{-16}\,{erg}/\RK is Boltzmann’s constant.
Second method
The second method invokes a mathematical trick. First, let’s rescale p^\alpha_i\equiv\sqrt{2mE}\>u^\alpha_i. We then have
D(E)={V^N\over N!}\,\Bigg(\!{\sqrt{2mE}\over h}\Bigg)^{\!Nd}\,{1\over E}\int\!\!d^{M}\!u\>\delta\big(u_1^2+u_2^2+\ldots + u_M^2 -1\big)\ .
Here we have written \Bu=(u\ns_1,u\ns_2,\ldots,u\ns_M) with M=Nd as a M-dimensional vector. We’ve also used the rule \delta(Ex)=E^{-1}\delta(x) for \delta-functions. We can now write
d^M\!u=u^{M-1}\,du\>d\Omega\nd_M\ ,
where d\Omega\nd_M is the M-dimensional differential solid angle. We now have our answer:3
D(E)={V^N\over N!}\,\Bigg(\!{\sqrt{2m}\over h}\Bigg)^{\!Nd}\,E\nsub^{{1\over 2}Nd-1}\cdot \half\,\Omega\nd_{Nd}\ . \label{nrdos}
What remains is for us to compute \Omega\nd_M, the total solid angle in M dimensions. We do this by a nifty mathematical trick. Consider the integral
\begin{split} \CI\ns_M&=\int\!\!d^M\!u\>e^{-u^2} = \Omega\nd_M\int\limits_0^\infty\!\!du\>u^{M-1}\,e^{-\Bu^2}\\ &=\half\Omega\nd_M\!\int\limits_0^\infty\!\!ds\>s\nsub^{{1\over 2}M-1}\,e^{-s}=\half\Omega\nd_M\,\RGamma\big(\half M\big)\ , \end{split}
where s=u^2, and where
\RGamma(z)=\int\limits_0^\infty\!\!dt\,t^{z-1}\,e^{-t}
is the Gamma function, which satisfies z\,\RGamma(z)=\RGamma(z+1).4 On the other hand, we can compute \CI\nd_M in Cartesian coordinates, writing
\CI\ns_M=\left(\int\limits_{-\infty}^\infty\!\!\!du\ns_1\>e^{-u_1^2}\right)^{\!\!M}=\big(\sqrt{\pi}\big)^M\ .
Therefore
\Omega\nd_M={2\pi^{M/2}\over\RGamma(M/2)}\ .
We thereby obtain \Omega\nd_2=2\pi, \Omega\nd_3=4\pi, \Omega\nd_4=2\pi^2, , the first two of which are familiar.
Arbitrariness in the definition of S(E)
Note that D(E) has dimensions of inverse energy, so one might ask how we are to take the logarithm of a dimensionful quantity in Equation \ref{statent}. We must introduce an energy scale, such as \RDelta E in Equation \ref{DOSeqn}, and define {\tilde D}(E;\RDelta E)=D(E)\,\RDelta E and S(E;\RDelta E)\equiv\kB\ln {\tilde D}(E;\RDelta E). The definition of statistical entropy then involves the arbitrary parameter \RDelta E, however this only affects S(E) in an additive way. That is,
S(E,V,N;\RDelta E\ns_1) = S(E,V,N;\RDelta E\ns_2) + \kB\ln\!\bigg({\RDelta E\ns_1\over \RDelta E\ns_2}\bigg)\ .
Note that the difference between the two definitions of S depends only on the ratio \RDelta E\ns_1/\RDelta E\ns_2, and is independent of E, V, and N.
Ultra-relativistic ideal gas
Consider an ultrarelativistic ideal gas, with single particle dispersion \ve(p)=cp. We then have
\begin{split} Z(\beta)&={V^N\over N!}{\Omega^N_d\over h^Nd}\left(\int\limits_0^\infty\!\!dp\>p^{d-1}\>e^{-\beta cp}\right)^{\!\!N}\\ &={V^N\over N!}\bigg({\RGamma(d)\,\Omega_d\over c^d\,h^d\,\beta^d}\bigg)^{\!\!N}\ . \end{split}
The statistical entropy is S(E,V,N)=\kB\ln D(E,V,N)=N\kB\,\phi\big(\frac{E}{N},\frac{V}{N}\big), with
\phi\bigg({E\over N}\, , \,{V\over N}\bigg)=d\,\ln\!\bigg({E\over N}\bigg) + \ln\! \bigg({V\over N}\bigg) + \ln\!\bigg({\Omega_d\,\RGamma(d)\over (dhc)^d}\bigg) + (d+1) \label{phiurel}
Discrete systems
For classical systems where the energy levels are discrete, the states of the system \sket{\Bsigma} are labeled by a set of discrete quantities \{\sigma\ns_1,\sigma\ns_2,\ldots\}, where each variable \sigma\ns_i takes discrete values. The number of ways of configuring the system at fixed energy E is then
\ROmega(E,N)=\sum_\Bsigma\delta\ns_{\HH(\Bsigma),E}\ ,
where the sum is over all possible configurations. Here N labels the total number of particles. For example, if we have N spin-\half particles on a lattice which are placed in a magnetic field H, so the individual particle energy is \ve\ns_i=-\mu\ns_0 H\sigma, where \sigma=\pm 1, then in a configuration in which N\ns_\uar particles have \sigma\ns_i=+1 and N\ns_\dar=N-N\ns_\uar particles have \sigma\ns_i=-1, the energy is E=(N\ns_\dar-N\ns_\uar)\mu\ns_0 H. The number of configurations at fixed energy E is
\ROmega(E,N)={N\choose N\ns_\uar} = {N!\over \big({N\over 2} - {E\over 2\mu\ns_0 H}\big)! \, \big({N\over 2} + {E\over 2\mu\ns_0 H}\big)!}\ ,
since N\ns_{\uar/\dar}={N\over 2}\mp {E\over 2\mu\ns_0 H}. The statistical entropy is S(E,N)=\kB\ln\ROmega(E,N).


