7.3: Mean Field Theory

$\newcommand\bes{\begin{equation}\begin{split}}$
$\newcommand\ltwid{\propto}$
$\newcommand\ees{\end{split}\end{equation}}$
$\newcommand\mib{\mathbf}$
$\newcommand\Sa{\textsf a}$
$\newcommand\Sb{\textsf b}$
$\newcommand\Sc{\textsf c}$
$\newcommand\Sd{\textsf d}$
$\newcommand\Se{\textsf e}$
$\newcommand\Sf{\textsf f}$
$\newcommand\Sg{\textsf g}$
$\newcommand\Sh{\textsf h}$
$\newcommand\Si{\textsf i}$
$\newcommand\Sj{\textsf j}$
$\newcommand\Sk{\textsf k}$
$\newcommand\Sl{\textsf l}$
$\newcommand\Sm{\textsf m}$
$\newcommand\Sn{\textsf n}$
$\newcommand\So{\textsf o}$
$\newcommand\Sp{\textsf p}$
$\newcommand\Sq{\textsf q}$
$\newcommand\Sr{\textsf r}$
$\newcommand\Ss{\textsf s}$
$\newcommand\St{\textsf t}$
$\newcommand\Su{\textsf u}$
$\newcommand\Sv{\textsf v}$
$\newcommand\Sw{\textsf w}$
$\newcommand\Sx{\textsf x}$
$\newcommand\Sy{\textsf y}$
$\newcommand\Sz{\textsf z}$
$\newcommand\SA{\textsf A}$
$\newcommand\SB{\textsf B}$
$\newcommand\SC{\textsf C}$
$\newcommand\SD{\textsf D}$
$\newcommand\SE{\textsf E}$
$\newcommand\SF{\textsf F}$
$\newcommand\SG{\textsf G}$
$\newcommand\SH{\textsf H}$
$\newcommand\SI{\textsf I}$
$\newcommand\SJ{\textsf J}$
$\newcommand\SK{\textsf K}$
$\newcommand\SL{\textsf L}$
$\newcommand\SM{\textsf M}$
$\newcommand\SN{\textsf N}$
$\newcommand\SO{\textsf O}$
$\newcommand\SP{\textsf P}$
$\newcommand\SQ{\textsf Q}$
$\newcommand\SR{\textsf R}$
$\newcommand\SS{\textsf S}$
$\newcommand\ST{\textsf T}$
$\newcommand\SU{\textsf U}$
$\newcommand\SV{\textsf V}$
$\newcommand\SW{\textsf W}$
$\newcommand\SX{\textsf X}$
$\newcommand\SY{\textsf Y}$
$\newcommand\SZ{\textsf Z}$
$\newcommand\Ha{\hat a}$
$\newcommand\Hb{\hat b}$
$\newcommand\Hc{\hat c}$
$\newcommand\Hd{\hat d}$
$\newcommand\He{\hat e}$
$\newcommand\Hf{\hat f}$
$\newcommand\Hg{\hat g}$
$\newcommand\Hh{\hat h}$
$\newcommand\Hi{\hat \imath}$
$\newcommand\Hj{\hat \jmath}$
$\newcommand\Hk{\hat k}$
$\newcommand\Hl{\hat l}$
$\newcommand\Hm{\hat m}$
$\newcommand\Hn{\hat n}$
$\newcommand\Ho{\hat o}$
$\newcommand\Hp{\hat p}$
$\newcommand\Hq{\hat q}$
$\newcommand\Hr{\hat r}$
$\newcommand\Hs{\hat s}$
$\newcommand\Ht{\hat t}$
$\newcommand\Hu{\hat u}$
$\newcommand\Hv{\hat v}$
$\newcommand\Hw{\hat w}$
$\newcommand\Hx{\hat x}$
$\newcommand\Hy{\hat y}$
$\newcommand\Hz{\hat z}$
$\newcommand\HA{\hat A}$
$\newcommand\HB{\hat B}$
$\newcommand\HC{\hat C}$
$\newcommand\HD{\hat D}$
$\newcommand\HE{\hat E}$
$\newcommand\HF{\hat F}$
$\newcommand\HG{\hat G}$
$\newcommand\HH{\hat H}$
$\newcommand\HI{\hat I}$
$\newcommand\HJ{\hat J}$
$\newcommand\HK{\hat K}$
$\newcommand\HL{\hat L}$
$\newcommand\HM{\hat M}$
$\newcommand\HN{\hat N}$
$\newcommand\HO{\hat O}$
$\newcommand\HP{\hat P}$
$\newcommand\HQ{\hat Q}$
$\newcommand\HR{\hat R}$
$\newcommand\HS{\hat S}$
$\newcommand\HT{\hat T}$
$\newcommand\HU{\hat U}$
$\newcommand\HV{\hat V}$
$\newcommand\HW{\hat W}$
$\newcommand\HX{\hat X}$
$\newcommand\HY{\hat Y}$
$\newcommand\HZ{\hat Z}$
$\newcommand\Halpha{\hat\alpha}$
$\newcommand\Hbeta{\hat\beta}$
$\newcommand\Hgamma{\hat\gamma}$
$\newcommand\Hdelta{\hat\delta}$
$\newcommand\Hepsilon{\hat\epsilon}$
$\newcommand\Hvarepsilon{\hat\varepsilon}$
$\newcommand\Hzeta{\hat\zeta}$
$\newcommand\Heta{\hat\eta}$
$\newcommand\Htheta{\hat\theta}$
$\newcommand\Hvartheta{\hat\vartheta}$
$\newcommand\Hiota{\hat\iota}$
$\newcommand\Hkappa{\hat\kappa}$
$\newcommand\Hlambda{\hat\lambda}$
$\newcommand\Hmu{\hat\mu}$
$\newcommand\Hnu{\hat\nu}$
$\newcommand\Hxi{\hat\xi}$
$\newcommand\Hom{\hat\omicron}$
$\newcommand\Hpi{\hat\pi}$
$\newcommand\Hvarpi{\hat\varpi}$
$\newcommand\Hrho{\hat\rho}$
$\newcommand\Hvarrho{\hat\varrho}$
$\newcommand\Hsigma{\hat\sigma}$
$\newcommand\Hvarsigma{\hat\varsigma}$
$\newcommand\Htau{\var\tau}$
$\newcommand\Hupsilon{\hat\upsilon}$
$\newcommand\Hphi{\hat\phi}$
$\newcommand\Hvarphi{\hat\varphi}$
$\newcommand\Hchi{\hat\chi}$
$\newcommand\Hxhi{\hat\xhi}$
$\newcommand\Hpsi{\hat\psi}$
$\newcommand\Homega{\hat\omega}$
$\newcommand\HGamma{\hat\Gamma}$
$\newcommand\HDelta{\hat\Delta}$
$\newcommand\HTheta{\hat\Theta}$
$\newcommand\HLambda{\hat\Lambda}$
$\newcommand\HXi{\hat\Xi}$
$\newcommand\HPi{\hat\Pi}$
$\newcommand\HSigma{\hat\Sigma}$
$\newcommand\HUps{\hat\Upsilon}$
$\newcommand\HPhi{\hat\Phi}$
$\newcommand\HPsi{\hat\Psi}$
$\newcommand\HOmega{\hat\Omega}$
$\newcommand\xhat{\hat\Bx}$
$\newcommand\yhat{\hat\By}$
$\newcommand\zhat{\hat\Bz}$
$\newcommand\ehat{\hat\Be}$
$\newcommand\khat{\hat\Bk}$
$\newcommand\nhat{\hat\Bn}$
$\newcommand\rhat{\hat\Br}$
$\newcommand\phihat{\hat\Bphi}$
$\newcommand\thetahat{\hat\Btheta}$
$\newcommand\MA{\mathbb A}$
$\newcommand\MB{\mathbb B}$
$\newcommand\MC{\mathbb C}$
$\newcommand\MD{\mathbb D}$
$\newcommand\ME{\mathbb E}$
$\newcommand\MF{\mathbb F}$
$\newcommand\MG{\mathbb G}$
$\newcommand\MH{\mathbb H}$
$\newcommand\MI{\mathbb I}$
$\newcommand\MJ{\mathbb J}$
$\newcommand\MK{\mathbb K}$
$\newcommand\ML{\mathbb L}$
$\newcommand\MM{\mathbb M}$
$\newcommand\MN{\mathbb N}$
$\newcommand\MO{\mathbb O}$
$\newcommand\MP{\mathbb P}$
$\newcommand\MQ{\mathbb Q}$
$\newcommand\MR{\mathbb R}$
$\newcommand\MS{\mathbb S}$
$\newcommand\MT{\mathbb T}$
$\newcommand\MU{\mathbb U}$
$\newcommand\MV{\mathbb V}$
$\newcommand\MW{\mathbb W}$
$\newcommand\MX{\mathbb X}$
$\newcommand\MY{\mathbb Y}$
$\newcommand\MZ{\mathbb Z}$
$\newcommand\CA{\mathcal A}$
$\newcommand\CB{\mathcal B}$
$\newcommand\CC{\mathcal C}$
$\newcommand\CD{\mathcal D}$
$\newcommand\CE{\mathcal E}$
$\newcommand\CF{\mathcal F}$
$\newcommand\CG{\mathcal G}$
$\newcommand\CH{\mathcal H}$
$\newcommand\CI{\mathcal I}$
$\newcommand\CJ{\mathcal J}$
$\newcommand\CK{\mathcal K}$
$\newcommand\CL{\mathcal L}$
$\newcommand\CM{\mathcal M}$
$\newcommand\CN{\mathcal N}$
$\newcommand\CO{\mathcal O}$
$\newcommand\CP{\mathcal P}$
$\newcommand\CQ{\mathcal Q}$
$\newcommand\CR{\mathcal R}$
$\newcommand\CS{\mathcal S}$
$\newcommand\CT{\mathcal T}$
$\newcommand\CU{\mathcal U}$
$\newcommand\CV{\mathcal V}$
$\newcommand\CW{\mathcal W}$
$\newcommand\CX{\mathcal X}$
$\newcommand\CY{\mathcal Y}$
$\newcommand\CZ{\mathcal Z}$
$\newcommand\Fa{\mathfrak a}$
$\newcommand\Fb{\mathfrak b}$
$\newcommand\Fc{\mathfrak c}$
$\newcommand\Fd{\mathfrak d}$
$\newcommand\Fe{\mathfrak e}$
$\newcommand\Ff{\mathfrak f}$
$\newcommand\Fg{\mathfrak g}$
$\newcommand\Fh{\mathfrak h}$
$\newcommand\Fi{\mathfrak i}$
$\newcommand\Fj{\mathfrak j}$
$\newcommand\Fk{\mathfrak k}$
$\newcommand\Fl{\mathfrak l}$
$\newcommand\Fm{\mathfrak m}$
$\newcommand\Fn{\mathfrak n}$
$\newcommand\Fo{\mathfrak o}$
$\newcommand\Fp{\mathfrak p}$
$\newcommand\Fq{\mathfrak q}$
$\newcommand\Fr{\mathfrak r}$
$\newcommand\Fs{\mathfrak s}$
$\newcommand\Ft{\mathfrak t}$
$\newcommand\Fu{\mathfrak u}$
$\newcommand\Fv{\mathfrak v}$
$\newcommand\Fw{\mathfrak w}$
$\newcommand\Fx{\mathfrak x}$
$\newcommand\Fy{\mathfrak y}$
$\newcommand\Fz{\mathfrak z}$
$\newcommand\FA{\mathfrak A}$
$\newcommand\FB{\mathfrak B}$
$\newcommand\FC{\mathfrak C}$
$\newcommand\FD{\mathfrak D}$
$\newcommand\FE{\mathfrak E}$
$\newcommand\FF{\mathfrak F}$
$\newcommand\FG{\mathfrak G}$
$\newcommand\FH{\mathfrak H}$
$\newcommand\FI{\mathfrak I}$
$\newcommand\FJ{\mathfrak J}$
$\newcommand\FK{\mathfrak K}$
$\newcommand\FL{\mathfrak L}$
$\newcommand\FM{\mathfrak M}$
$\newcommand\FN{\mathfrak N}$
$\newcommand\FO{\mathfrak O}$
$\newcommand\FP{\mathfrak P}$
$\newcommand\FQ{\mathfrak Q}$
$\newcommand\FR{\mathfrak R}$
$\newcommand\FS{\mathfrak S}$
$\newcommand\FT{\mathfrak T}$
$\newcommand\FU{\mathfrak U}$
$\newcommand\FV{\mathfrak V}$
$\newcommand\FW{\mathfrak W}$
$\newcommand\FX{\mathfrak X}$
$\newcommand\FY{\mathfrak Y}$
$\newcommand\FZ{\mathfrak Z}$
$\newcommand\Da{\dot a}$
$\newcommand\Db{\dot b}$
$\newcommand\Dc{\dot c}$
$\newcommand\Dd{\dot d}$
$\newcommand\De{\dot e}$
$\newcommand\Df{\dot f}$
$\newcommand\Dg{\dot g}$
$\newcommand\Dh{\dot h}$
$\newcommand\Di{\dot \imath}$
$\newcommand\Dj{\dot \jmath}$
$\newcommand\Dk{\dot k}$
$\newcommand\Dl{\dot l}$
$\newcommand\Dm{\dot m}$
$\newcommand\Dn{\dot n}$
$\newcommand\Do{\dot o}$
$\newcommand\Dp{\dot p}$
$\newcommand\Dq{\dot q}$
$\newcommand\Dr{\dot r}$
$\newcommand\Ds{\dot s}$
$\newcommand\Dt{\dot t}$
$\newcommand\Du{\dot u}$
$\newcommand\Dv{\dot v}$
$\newcommand\Dw{\dot w}$
$\newcommand\Dx{\dot x}$
$\newcommand\Dy{\dot y}$
$\newcommand\Dz{\dot z}$
$\newcommand\DA{\dot A}$
$\newcommand\DB{\dot B}$
$\newcommand\DC{\dot C}$
$\newcommand\DD{\dot D}$
$\newcommand\DE{\dot E}$
$\newcommand\DF{\dot F}$
$\newcommand\DG{\dot G}$
$\newcommand\DH{\dot H}$
$\newcommand\DI{\dot I}$
$\newcommand\DJ{\dot J}$
$\newcommand\DK{\dot K}$
$\newcommand\DL{\dot L}$
$\newcommand\DM{\dot M}$
$\newcommand\DN{\dot N}$
$\newcommand\DO{\dot O}$
$\newcommand\DP{\dot P}$
$\newcommand\DQ{\dot Q}$
$\newcommand\DR{\dot R}$
$\newcommand\DS{\dot S}$
$\newcommand\DT{\dot T}$
$\newcommand\DU{\dot U}$
$\newcommand\DV{\dot V}$
$\newcommand\DW{\dot W}$
$\newcommand\DX{\dot X}$
$\newcommand\DY{\dot Y}$
$\newcommand\DZ{\dot Z}$
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\Dmu{\dot\mu}$
$\newcommand\Dnu{\dot\nu}$
$\newcommand\Dxi{\dot\xi}$
$\newcommand\Dom{\dot\omicron}$
$\newcommand\Dpi{\dot\pi}$
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\Drho{\dot\rho}$
$\newcommand\Dvarrho{\dot\varrho}$
$\newcommand\Dsigma{\dot\sigma}$
$\newcommand\Dvarsigma{\dot\varsigma}$
$\newcommand\Dtau{\var\tau}$
$\newcommand\Dupsilon{\dot\upsilon}$
$\newcommand\Dphi{\dot\phi}$
$\newcommand\Dvarphi{\dot\varphi}$
$\newcommand\Dchi{\dot\chi}$
$\newcommand\Dpsi{\dot\psi}$
$\newcommand\Domega{\dot\omega}$
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\DLambda{\dot\Lambda}$
$\newcommand\DXi{\dot\Xi}$
$\newcommand\DPi{\dot\Pi}$
$\newcommand\DSigma{\dot\Sigma}$
$\newcommand\DUps{\dot\Upsilon}$
$\newcommand\DPhi{\dot\Phi}$
$\newcommand\DPsi{\dot\Psi}$
$\newcommand\DOmega{\dot\Omega}$
$\newcommand\Va{\vec a}$
$\newcommand\Vb{\vec b}$
$\newcommand\Vc{\vec c}$
$\newcommand\Vd{\vec d}$
$\newcommand\Ve{\vec e}$
$\newcommand\Vf{\vec f}$
$\newcommand\Vg{\vec g}$
$\newcommand\Vh{\vec h}$
$\newcommand\Vi{\vec \imath}$
$\newcommand\Vj{\vec \jmath}$
$\newcommand\Vk{\vec k}$
$\newcommand\Vl{\vec l}$
$\newcommand\Vm{\vec m}$
$\newcommand\Vn{\vec n}$
$\newcommand\Vo{\vec o}$
$\newcommand\Vp{\vec p}$
$\newcommand\Vq{\vec q}$
$\newcommand\Vr{\vec r}$
$\newcommand\Vs{\vec s}$
$\newcommand\Vt{\vec t}$
$\newcommand\Vu{\vec u}$
$\newcommand\Vv{\vec v}$
$\newcommand\Vw{\vec w}$
$\newcommand\Vx{\vec x}$
$\newcommand\Vy{\vec y}$
$\newcommand\Vz{\vec z}$
$\newcommand\VA{\vec A}$
$\newcommand\VB{\vec B}$
$\newcommand\VC{\vec C}$
$\newcommand\VD{\vec D}$
$\newcommand\VE{\vec E}$
$\newcommand\VF{\vec F}$
$\newcommand\VG{\vec G}$
$\newcommand\VH{\vec H}$
$\newcommand\VI{\vec I}$
$\newcommand\VJ{\vec J}$
$\newcommand\VK{\vec K}$
$\newcommand\VL{\vec L}$
$\newcommand\VM{\vec M}$
$\newcommand\VN{\vec N}$
$\newcommand\VO{\vec O}$
$\newcommand\VP{\vec P}$
$\newcommand\VQ{\vec Q}$
$\newcommand\VR{\vec R}$
$\newcommand\VS{\vec S}$
$\newcommand\VT{\vec T}$
$\newcommand\VU{\vec U}$
$\newcommand\VV{\vec V}$
$\newcommand\VW{\vec W}$
$\newcommand\VX{\vec X}$
$\newcommand\VY{\vec Y}$
$\newcommand\VZ{\vec Z}$
$\newcommand\Valpha{\vec\alpha}$
$\newcommand\Vbeta{\vec\beta}$
$\newcommand\Vgamma{\vec\gamma}$
$\newcommand\Vdelta{\vec\delta}$
$\newcommand\Vepsilon{\vec\epsilon}$
$\newcommand\Vvarepsilon{\vec\varepsilon}$
$\newcommand\Vzeta{\vec\zeta}$
$\newcommand\Veta{\vec\eta}$
$\newcommand\Vtheta{\vec\theta}$
$\newcommand\Vvartheta{\vec\vartheta}$
$\newcommand\Viota{\vec\iota}$
$\newcommand\Vkappa{\vec\kappa}$
$\newcommand\Vlambda{\vec\lambda}$
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\VTheta{\vec\Theta}$
$\newcommand\VLambda{\vec\Lambda}$
$\newcommand\VXi{\vec\Xi}$
$\newcommand\VPi{\vec\Pi}$
$\newcommand\VSigma{\vec\Sigma}$
$\newcommand\VUps{\vec\Upsilon}$
$\newcommand\VPhi{\vec\Phi}$
$\newcommand\VPsi{\vec\Psi}$
$\newcommand\VOmega{\vec\Omega}$
$\newcommand\BA{\mib A}$
$\newcommand\BB{\mib B}$
$\newcommand\BC{\mib C}$
$\newcommand\BD{\mib D}$
$\newcommand\BE{\mib E}$
$\newcommand\BF{\mib F}$
$\newcommand\BG{\mib G}$
$\newcommand\BH{\mib H}$
$\newcommand\BI{\mib I}}$
$\newcommand\BJ{\mib J}$
$\newcommand\BK{\mib K}$
$\newcommand\BL{\mib L}$
$\newcommand\BM{\mib M}$
$\newcommand\BN{\mib N}$
$\newcommand\BO{\mib O}$
$\newcommand\BP{\mib P}$
$\newcommand\BQ{\mib Q}$
$\newcommand\BR{\mib R}$
$\newcommand\BS{\mib S}$
$\newcommand\BT{\mib T}$
$\newcommand\BU{\mib U}$
$\newcommand\BV{\mib V}$
$\newcommand\BW{\mib W}$
$\newcommand\BX{\mib X}$
$\newcommand\BY{\mib Y}$
$\newcommand\BZ{\mib Z}$
$\newcommand\Ba{\mib a}$
$\newcommand\Bb{\mib b}$
$\newcommand\Bc{\mib c}$
$\newcommand\Bd{\mib d}$
$\newcommand\Be{\mib e}$
$\newcommand\Bf{\mib f}$
$\newcommand\Bg{\mib g}$
$\newcommand\Bh{\mib h}$
$\newcommand\Bi{\mib i}$
$\newcommand\Bj{\mib j}$
$\newcommand\Bk{\mib k}$
$\newcommand\Bl{\mib l}$
$\newcommand\Bm{\mib m}$
$\newcommand\Bn{\mib n}$
$\newcommand\Bo{\mib o}$
$\newcommand\Bp{\mib p}$
$\newcommand\Bq{\mib q}$
$\newcommand\Br{\mib r}$
$\newcommand\Bs{\mib s}$
$\newcommand\Bt{\mib t}$
$\newcommand\Bu{\mib u}$
$\newcommand\Bv{\mib v}$
$\newcommand\Bw{\mib w}$
$\newcommand\Bx{\mib x}$
$\newcommand\By{\mib y}$
$\newcommand\Bz{\mib z}$\)
$\newcommand\vrh{\varrho}$
$\newcommand\vsig{\varsigma}$
$\newcommand\ups{\upsilon}$
$\newcommand\eps{\epsilon}$
$\newcommand\ve{\varepsilon}$
$\newcommand\vth{\vartheta}$
$\newcommand\vphi{\varphi}$
$\newcommand\xhi{\chi}$
$\newcommand\Ups{\Upsilon}$
$\newcommand\Balpha{\mib\alpha}$
$\newcommand\Bbeta{\mib\beta}$
$\newcommand\Bgamma{\mib\gamma}$
$\newcommand\Bdelta{\mib\delta}$
$\newcommand\Beps{\mib\epsilon}$
$\newcommand\Bve{\mib\varepsilon}$
$\newcommand\Bzeta{\mib\zeta}$
$\newcommand\Beta{\mib\eta}$
$\newcommand\Btheta{\mib\theta}$
$\newcommand\Bvth{\mib\vartheta}$
$\newcommand\Biota{\mib\iota}$
$\newcommand\Bkappa{\mib\kappa}$
$\newcommand\Blambda{\mib\lambda}$
$\newcommand\Bmu{\mib\mu}$
$\newcommand\Bnu{\mib\nu}$
$\newcommand\Bxi{\mib\xi}$
$\newcommand\Bom{\mib\omicron}$
$\newcommand\Bpi{\mib\pi}$
$\newcommand\Bvarpi{\mib\varpi}$
$\newcommand\Brho{\mib\rho}$
$\newcommand\Bvrh{\mib\varrho}$
$\newcommand\Bsigma{\mib\sigma}$
$\newcommand\Bvsig{\mib\varsigma}$
$\newcommand\Btau{\mib\tau}$
$\newcommand\Bups{\mib\upsilon}$
$\newcommand\Bphi{\mib\phi}$
$\newcommand\Bvphi{\mib\vphi}$
$\newcommand\Bchi{\mib\chi}$
$\newcommand\Bpsi{\mib\psi}$
$\newcommand\Bomega{\mib\omega}$
$\newcommand\BGamma{\mib\Gamma}$
$\newcommand\BDelta{\mib\Delta}$
$\newcommand\BTheta{\mib\Theta}$
$\newcommand\BLambda{\mib\Lambda}$
$\newcommand\BXi{\mib\Xi}$
$\newcommand\BPi{\mib\Pi}$
$\newcommand\BSigma{\mib\Sigma}$
$\newcommand\BUps{\mib\Upsilon}$
$\newcommand\BPhi{\mib\Phi}$
$\newcommand\BPsi{\mib\Psi}$
$\newcommand\BOmega{\mib\Omega}$
$\newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}$
$\newcommand\RGamma{ \Gamma}$
$\newcommand\RDelta{ \Delta}$
$\newcommand\RTheta{ \Theta}$
$\newcommand\RLambda{ \Lambda}$
$\newcommand\RXi{ \Xi}$
$\newcommand\RPi{ \Pi}$
$\newcommand\RSigma{ \Sigma}$
$\newcommand\RUps{ \Upsilon}$
$\newcommand\RPhi{ \Phi}$
$\newcommand\RPsi{ \Psi}$
$\newcommand\ROmega{ \Omega}$
$\newcommand\RA{ A}$
$\newcommand\RB{ B}$
$\newcommand\RC{ C}$
$\newcommand\RD{ D}$
$\newcommand\RE{ E}$
$\newcommand\RF{ F}$
$\newcommand\RG{ G}$
$\newcommand\RH{ H}$
$\newcommand\RI{ I}$
$\newcommand\RJ{ J}$
$\newcommand\RK{ K}$
$\newcommand\RL{ L}$
$\newcommand { M}$
$\newcommand\RN{ N}$
$\newcommand\RO{ O}$
$\newcommand\RP{ P}$
$\newcommand\RQ{ Q}$
$\newcommand\RR{ R}$
$\newcommand\RS{ S}$
$\newcommand\RT{ T}$
$\newcommand\RU{ U}$
$\newcommand\RV{ V}$
$\newcommand\RW{ W}$
$\newcommand\RX{ X}$
$\newcommand\RY{ Y}$
$\newcommand\RZ{ Z}$
$\newcommand\Ra{ a}$
$\newcommand\Rb{ b}$
$\newcommand\Rc{ c}$
$\newcommand\Rd{ d}$
$\newcommand\Re{ e}$
$\newcommand\Rf{ f}$
$\newcommand\Rg{ g}$
$\newcommand\Rh{ h}$
$\newcommand\Ri{ i}$
$\newcommand\Rj{ j}$
$\newcommand\Rk{ k}$
$\newcommand\Rl{ l}$
$\newcommand { m}$
$\newcommand\Rn{ n}$
$\newcommand\Ro{ o}$
$\newcommand\Rp{ p}$
$\newcommand\Rq{ q}$
$\newcommand\Rr{ r}$
$\newcommand\Rs{ s}$
$\newcommand\Rt{ t}$
$\newcommand\Ru{ u}$
$\newcommand\Rv{ v}$
$\newcommand\Rw{ w}$
$\newcommand\Rx{ x}$
$\newcommand\Ry{ y}$
$\newcommand\Rz{ z}$
$\newcommand\BBA{\boldsymbol\RA}$
$\newcommand\BBB{\boldsymbol\RB}$
$\newcommand\BBC{\boldsymbol\RC}$
$\newcommand\BBD{\boldsymbol\RD}$
$\newcommand\BBE{\boldsymbol\RE}$
$\newcommand\BBF{\boldsymbol\RF}$
$\newcommand\BBG{\boldsymbol\RG}$
$\newcommand\BBH{\boldsymbol\RH}$
$\newcommand\BBI{\boldsymbol\RI}$
$\newcommand\BBJ{\boldsymbol\RJ}$
$\newcommand\BBK{\boldsymbol\RK}$
$\newcommand\BBL{\boldsymbol\RL}$
$\newcommand\BBM{\boldsymbol }$
$\newcommand\BBN{\boldsymbol\RN}$
$\newcommand\BBO{\boldsymbol\RO}$
$\newcommand\BBP{\boldsymbol\RP}$
$\newcommand\BBQ{\boldsymbol\RQ}$
$\newcommand\BBR{\boldsymbol\RR}$
$\newcommand\BBS{\boldsymbol\RS}$
$\newcommand\BBT{\boldsymbol\RT}$
$\newcommand\BBU{\boldsymbol\RU}$
$\newcommand\BBV{\boldsymbol\RV}$
$\newcommand\BBW{\boldsymbol\RW}$
$\newcommand\BBX{\boldsymbol\RX}$
$\newcommand\BBY{\boldsymbol\RY}$
$\newcommand\BBZ{\boldsymbol\RZ}$
$\newcommand\BBa{\boldsymbol\Ra}$
$\newcommand\BBb{\boldsymbol\Rb}$
$\newcommand\BBc{\boldsymbol\Rc}$
$\newcommand\BBd{\boldsymbol\Rd}$
$\newcommand\BBe{\boldsymbol\Re}$
$\newcommand\BBf{\boldsymbol\Rf}$
$\newcommand\BBg{\boldsymbol\Rg}$
$\newcommand\BBh{\boldsymbol\Rh}\}$
$\newcommand\BBi{\boldsymbol\Ri}$
$\newcommand\BBj{\boldsymbol\Rj}$
$\newcommand\BBk{\boldsymbol\Rk}$
$\newcommand\BBl{boldsymbol\Rl}$
$\newcommand\BBm{\boldsymbol }$
$\newcommand\BBn{\boldsymbol\Rn}$
$\newcommand\BBo{\boldsymbol\Ro}$
$\newcommand\BBp{\boldsymbol\Rp}$
$\newcommand\BBq{\boldsymbol\Rq}$
$\newcommand\BBr{\boldsymbol\Rr}$
$\newcommand\BBs{\boldsymbol\Rs}$
$\newcommand\BBt{\boldsymbol\Rt}$
$\newcommand\BBu{\boldsymbol\Ru}$
$\newcommand\BBv{\boldsymbol\Rv}$
$\newcommand\BBw{\boldsymbol\Rw}$
$\newcommand\BBx{\boldsymbol\Rx}$
$\newcommand\BBy{\boldsymbol\Ry}$
$\newcommand\BBz{\boldsymbol\Rz}$
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
$\newcommand\bnabla{\boldsymbol{\nabla}}$
$\newcommand\Bell{\boldsymbol\ell}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\newcommand\ns{^\vphantom{*}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}$
$\newcommand\izpi{\int\limits_{0}^{\infty}\!\!}$
$\newcommand\etc{\it etc.\/}$
$\newcommand\etal{\it et al.\/}$
$\newcommand\opcit{\it op. cit.\/}$
$\newcommand\ie{\it i.e.\/}$
$\newcommand\Ie{\it I.e.\/}$
$\newcommand\viz{\it viz.\/}$
$\newcommand\eg{\it e.g.\/}$
$\newcommand\Eg{\it E.g.\/}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\def\sss#1{\scriptscriptstyle #1}$
$\def\ss#1{\scriptstyle #1}$
$\def\ssr#1{\scriptstyle #1}$
$\def\ssf#1{\scriptstyle #1}$
$\newcommand\NA{N_{\ssr{\!A}}}$
$\newcommand\lala{\langle\!\langle}$
$\newcommand\rara{\rangle\!\rangle}$
$\newcommand\blan{\big\langle}$
$\newcommand\bran{\big\rangle}$
$\newcommand\Blan{\Big\langle}$
$\newcommand\Bran{\Big\rangle}$
$\newcommand\intl{\int\limits}$
$\newcommand\half{\frac{1}{2}}$
$\newcommand\third{\frac{1}{3}}$
$\newcommand\fourth{\frac{1}{4}}$
$\newcommand\eighth{\frac{1}{8}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\undertext#1{$\underline{\hbox{#1}}$}$
$\newcommand\Tra{\mathop{\textsf{Tr}}\,}$
$\newcommand\det{\mathop{\textsf{det}}\,}$
$\def\tket#1{|  #1 \rangle}$
$\def\tbra#1{\langle #1|}$
$\def\tbraket#1#2{\langle #1  |   #2 \rangle}$
$\def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}$
$\def\sket#1{|  \, #1 \,  \rangle}$
$\def\sbra#1{\langle \,  #1 \, |}$
$\def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}$
$\def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}$
$\def\ket#1{\big| \, #1\, \big\rangle}$
$\def\bra#1{\big\langle \, #1 \, \big|}$
$\def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}$
$\def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}$
$\newcommand\pz{\partial}$
$\newcommand\pzb{\bar{\partial}}$
$\newcommand\svph{\vphantom{\int}}$
$\newcommand\vph{\vphantom{\sum_i}}$
$\newcommand\bvph{\vphantom{\sum_N^N}}$
$\newcommand\nd{^{\vphantom{\dagger}}}$
$\newcommand\ns{^{\vphantom{*}}}$
$\newcommand\yd{^\dagger}$
$\newcommand\zb{\bar z}$
$\newcommand\zdot{\dot z}$
$\newcommand\zbdot{\dot{\bar z}}$
$\newcommand\kB{k_{\sss{B}}}$
$\newcommand\kT{k_{\sss{B}}T}$
$\newcommand\gtau{g_\tau}$
$\newcommand\Htil{\tilde H}$
$\newcommand\pairo{(\phi\nd_0,J\nd_0)}$
$\newcommand\pairm{(\phi\nd_0,J)}$
$\newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}$
$\newcommand\pairmb{(\Bphi\nd_0,\BJ)}$
$\newcommand\pair{(\phi,J)}$
$\newcommand\Hz{H\nd_0}$
$\newcommand\Ho{H\nd_1}$
$\newcommand\Htz{\Htil\nd_0}$
$\newcommand\Hto{\Htil\nd_1}$
$\newcommand\oc{\omega_\Rc}$

$\newcommand \gtwid{\approx}$

$\newcommand\index{\textsf{ind}}$
$\newcommand\csch{\,{ csch\,}}$
$\newcommand\ctnh{\,{ ctnh\,}}$
$\newcommand\ctn{\,{ ctn\,}}$
$\newcommand\sgn{\,{ sgn\,}}$
$\def\tmapright#1{\xrightarrow \limits^{#1}}$
$\def\bmapright#1{\xrightarrow\limits_{#1}}$
$\newcommand\hfb{\hfill\break}$
$\newcommand\Rep{\textsf{Re}\,}$
$\newcommand\Imp{\textsf{Im}\,}$
$\newcommand\ncdot{\!\cdot\!}$
$\def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }$
$\def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }$
$\newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}$

$\def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}$
$\def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}$
$\def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}$
$\def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}$
$\newcommand\subA{\ns_\ssr{A}}$
$\newcommand\subB{\ns_\ssr{B}}$
$\newcommand\subC{\ns_\ssr{C}}$
$\newcommand\subD{\ns_\ssr{D}}$
$\newcommand\subAB{\ns_\ssr{AB}}$
$\newcommand\subBC{\ns_\ssr{BC}}$
$\newcommand\subCD{\ns_\ssr{CD}}$
$\newcommand\subDA{\ns_\ssr{DA}}$
$\def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }$
$\def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}$
$\newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}$
$\newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}$
$\newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}$
$\newcommand\cds{\,\bullet\,}$
$\newcommand\ccs{\,\circ\,}$
$\newcommand\nsub{_{\vphantom{\dagger}}}$
$\newcommand\rhohat{\hat\rho}$
$\newcommand\vrhhat{\hat\vrh}$
$\newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}$
$\newcommand\brangle{\big\rangle}$
$\newcommand\blangle{\big\langle}$
$\newcommand\vet{\tilde\ve}$
$\newcommand\zbar{\bar z}$
$\newcommand\ftil{\tilde f}$
$\newcommand\XBE{\RXi\ns_\ssr{BE}}$
$\newcommand\XFD{\RXi\ns_\ssr{FD}}$
$\newcommand\OBE{\Omega\ns_\ssr{BE}}$
$\newcommand\OFD{\Omega\ns_\ssr{FD}}$
$\newcommand\veF{\ve\ns_\RF}$
$\newcommand\kF{k\ns_\RF}$
$\newcommand\kFu{k\ns_{\RF\uar}}$
$\newcommand\SZ{\textsf Z}}$ \( \newcommand\kFd{k\ns_{\RF\dar}\)
$\newcommand\muB{\mu\ns_\ssr{B}}$
$\newcommand\mutB{\tilde\mu}\ns_\ssr{B}$
$\newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}$
$\newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}$
$\newcommand\xhiOZ{\xhi^\ssr{OZ}}$
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\jhz{\HJ(0)}$
$\newcommand\nda{\nd_\alpha}$
$\newcommand\ndap{\nd_{\alpha'}}$
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.03:_Mean_Field_Theory), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\msa{m\ns_\ssr{A}}$
$\newcommand\msb{m\ns_\ssr{B}}$
$\newcommand\mss{m\ns_\Rs}$
$\newcommand\HBx{\hat\Bx}$
$\newcommand\HBy{\hat\By}$
$\newcommand\HBz{\hat\Bz}$
$\newcommand\thm{\theta\ns_m}$
$\newcommand\thp{\theta\ns_\phi}$
$\newcommand\mtil{\widetilde m}$
$\newcommand\phitil{\widetilde\phi}$
$\newcommand\delf{\delta\! f}$
$\newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}$
$\newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}$
$\newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}$
$\newcommand\vbar{\bar v}$
$\newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}$
$\newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}$
$\newcommand\gla{g\nd_{\RLambda\nd}}$
$\newcommand\TA{T\ns_\ssr{A}}$
$\newcommand\TB{T\ns_\ssr{B}}$
$\newcommand\ncdot{\!\cdot\!}$
$\newcommand\NS{N\ns_{\textsf S}}$

Consider the Ising model Hamiltonian,

$$\HH=-J\sum_{\langle ij\rangle} \sigma_i\,\sigma_j -H\sum_i \sigma_i\ ,$$

where the first sum on the RHS is over all links of the lattice. Each spin can be either ‘up’ ($\sigma=+1$) or ‘down’ ($\sigma=-1$). We further assume that the spins are located on a Bravais lattice⁸ and that the coupling $J_{ij}=J\big( |\BR_i - \BR_j|\big)$, where $\BR_i$ is the position of the $i^{\ssr{th}}$ spin.

On each site $i$ we decompose $\sigma\ns_i$ into a contribution from its thermodynamic average and a fluctuation term,

$$\sigma\ns_i=\langle\sigma\ns_i\rangle + \delta\sigma\ns_i\ .$$

We will write $\langle\sigma\ns_i\rangle\equiv m$, the local magnetization (dimensionless), and assume that $m$ is independent of position $i$. Then

$$\begin{split} \sigma\ns_i\,\sigma\ns_j &= (m+\delta\sigma\ns_i)\,(m+\delta\sigma\ns_j)\\ &=m^2 + m\,(\delta\sigma\ns_i + \delta\sigma\ns_j) + \delta\sigma\ns_i\,\delta\sigma\ns_j\\ &=-m^2 + m\,(\sigma\ns_i + \sigma\ns_j) + \delta\sigma\ns_i\,\delta\sigma\ns_j\ . \end{split}$$

The last term on the RHS of the second equation above is quadratic in the fluctuations, and we assume this to be negligibly small. Thus, we obtain the mean field Hamiltonian

$$\HH\ns_{\ssr{MF}}=\half NzJ\,m^2- \big(H+zJm\big)\sum_i\sigma_i\ ,$$

where $N$ is the total number of lattice sites. The first term is a constant, although the value of $m$ is yet to be determined. The Boltzmann weights are then completely determined by the second term, which is just what we would write down for a Hamiltonian of noninteracting spins in an effective ‘mean field’

$$H\ns_{eff}=H+zJm\ .$$

In other words, $H\ns_{eff}=H\ns_{ext} + H\ns_{int}$, where the external field is applied field $H\ns_{ext}=H$, and the ‘internal field’ is $H\ns_{int}=zJm$. The internal field accounts for the interaction with the average values of all other spins coupled to a spin at a given site, hence it is often called the ‘mean field’. Since the spins are noninteracting, we have

$$m={e^{\beta H\ns_{eff}} - e^{-\beta H\ns_{eff}} \over e^{\beta H\ns_{eff}} + e^{-\beta H\ns_{eff}} } =\tanh\!\bigg({H+zJm\over\kT}\bigg)\ .$$

It is a simple matter to solve for the free energy, given the noninteracting Hamiltonian $\HH\ns_{\ssr{MF}}$. The partition function is

$$Z=\Tra e^{-\beta\HH\ns_{\ssr{MF}}}=e^{-\half \beta NzJ\,m^2} \bigg(\sum_\sigma e^{\beta (H+zJm)\sigma}\bigg)^{\!N} =e^{-\beta F}\ .$$

We now define dimensionless variables:

$$f\equiv {F\over NzJ}\qquad,\qquad\theta\equiv {\kT\over zJ}\qquad,\qquad h\equiv {H\over zJ}\ ,$$

and obtain the dimensionless free energy

$$f(m,h,\theta)=\half m^2 - \theta\,\ln \bigg(e^{(m+h)/\theta} + e^{-(m+h)/\theta}\bigg)\ . \label{fergsca}$$

Differentiating with respect to $m$ gives the mean field equation,

$$m=\tanh\Big({m+h\over \theta}\Big)\ , \label{isingmft}$$

which is equivalent to the self-consistency requirement, $m=\langle \sigma_i\rangle$.

$h=0$

When $h=0$ the mean field equation becomes

$$m=\tanh\Big({m\over \theta}\Big)\ .$$

This nonlinear equation can be solved graphically, as in the top panel of Figure $\ref{IMFzh}$. The RHS in a tanh function which gets steeper with decreasing $t$. If, at $m=0$, the slope of $\tanh(m/\theta)$ is smaller than unity, then the curve $y=\tanh(m/h)$ will intersect $y=m$ only at $m=0$. However, if the slope is larger than unity, there will be three such intersections. Since the slope is $1/\theta$, we identify $\theta\ns_\Rc=1$ as the mean field transition temperature.

Figure $\PageIndex{1}$: Results for $h=0$. Upper panels: graphical solution to self-consistency equation $m=\tanh(m/\theta)$ at temperatures $\theta=0.65$ (blue) and $\theta=1.5$ (dark red). Lower panel: mean field free energy, with energy shifted by $\theta\ln 2$ so that $f(m=0,\theta)=0$.

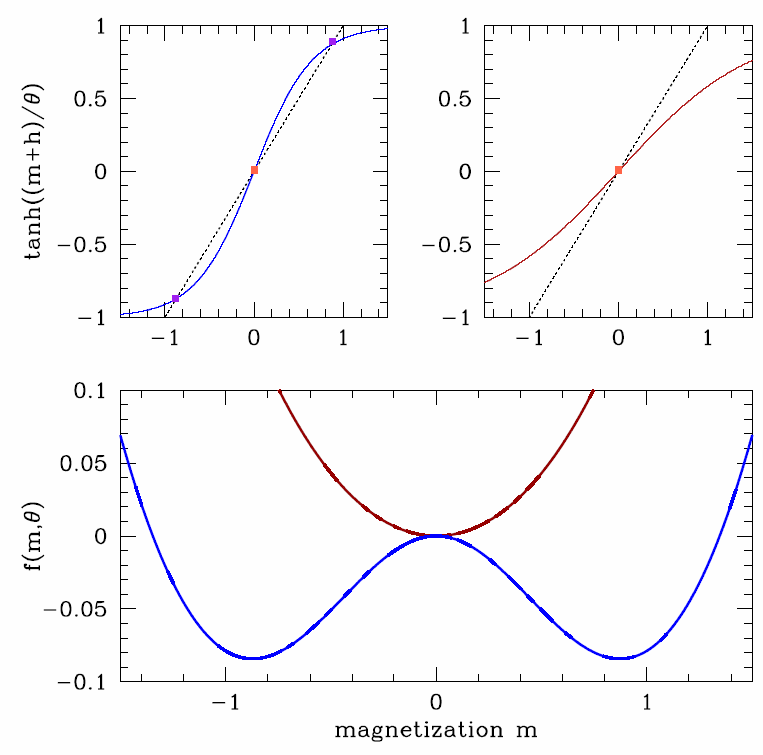
In the low temperature phase $\theta<1$, there are three solutions to the mean field equations. One solution is always at $m=0$. The other two solutions must be related by the $m\leftrightarrow -m$ symmetry of the free energy (when $h=0$). The exact free energies are plotted in the bottom panel of Figure $\PageIndex{1}$, but it is possible to make analytical progress by assuming $m$ is small and Taylor expanding the free energy $f(m,\theta)$ in powers of $m$:

$$\begin{split} f(m,\theta)&=\half m^2 -\theta\ln2 -\theta\,\ln\cosh\Big({m\over \theta}\Big)\\ &=-\theta\,\ln 2 + \half\,(1-\theta^{-1})\,m^2 +{m^4\over 12\,\theta^3} - {m^6\over 45\,\theta^5} + \ldots\ . \end{split}$$

Note that the sign of the quadratic term is positive for $\theta>1$ and negative for $\theta<1$. Thus, the shape of the free energy $f(m,\theta)$ as a function of $m$ qualitatively changes at this point, $\theta\ns_\Rc=1$, the mean field transition temperature, also known as the critical temperature.

For $\theta>\theta\ns_\Rc$, the free energy $f(m,\theta)$ has a single minimum at $m=0$. Below $\theta\ns_\Rc$, the curvature at $m=0$ reverses, and $m=0$ becomes a local maximum. There are then two equivalent minima symmetrically displaced on either side of $m=0$. Differentiating with respect to $m$, we find these local minima. For $\theta<\theta\ns_\Rc$, the local minima are found at

$$m^2=3\theta^2(1-\theta) = 3 (1-\theta) + \CO\big((1-\theta)^2\big)\ .$$

Thus, we find for $|\theta-1|\ll 1$,

$$m(\theta,h=0)=\pm\sqrt{3}\,\big(1-\theta\big)_+^{1/2}\ ,$$

where the $+$ subscript indicates that this solution is only for $1-\theta>0$. For $\theta>1$ the only solution is $m=0$. The exponent with which $m(\theta)$ vanishes as $\theta\to \theta^-_\Rc$ is denoted $\beta$. $m(\theta,h=0) \propto(\theta\ns_\Rc-\theta)_+^\beta$.

Specific heat

We can now expand the free energy $f(\theta,h=0)$. We find

$$f(\theta,h=0)=\begin{cases} -\theta\ln 2 & \hbox{if $\theta>\theta\ns_\Rc$}\\ -\theta\ln 2-{3\over 4} (1-\theta)^2 + \CO\big( (1-\theta)^4\big) & \hbox{if $\theta<\theta\ns_\Rc$}\ . \end{cases}$$

Thus, if we compute the heat capacity, we find in the vicinity of $\theta=\theta\ns_\Rc$

$$c\ns_V=-\theta\,{\pz^2\!f\over\pz \theta^2}=\begin{cases} 0 & \hbox{if $\theta>\theta\ns_\Rc$}\\ {3\over 2} & \hbox{if $\theta<\theta\ns_\Rc$}\ . \end{cases}$$

Thus, the specific heat is discontinuous at $\theta=\theta\ns_\Rc$. We emphasize that this is only valid near $\theta=\theta\ns_\Rc=1$. The general result valid for all $\theta$ is⁹

$$c\ns_V(\theta)={1\over \theta}\cdot{m^2(\theta)-m^4(\theta)\over \theta-1+m^2(\theta)}\ ,$$

With this expression one can check both limits $\theta\to 0$ and $\theta\to \theta\ns_\Rc$. As $\theta\to 0$ the magnetization saturates and one has $m^2(\theta) \simeq 1-4\,e^{-2/\theta}$. The numerator then vanishes as $e^{-2/\theta}$, which overwhelms the denominator that itself vanishes as $\theta^2$. As a result, $c\ns_V(\theta\to 0) =0$, as expected. As $\theta\to 1$, invoking $m^2\simeq 3(1-\theta)$ we recover $c\ns_V(\theta_\Rc^-)=\frac{3}{2}$.

In the theory of critical phenomena, $c\ns_V(\theta)\propto |\theta-\theta\ns_\Rc|^{-\alpha}$ as $\theta\to \theta\ns_\Rc$. We see that mean field theory yields $\alpha=0$.

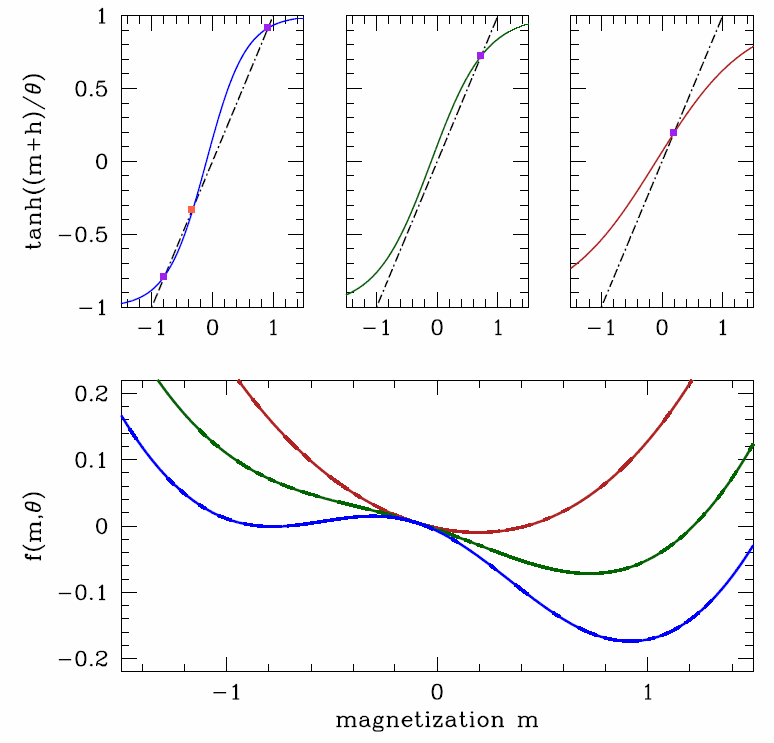
Figure $\PageIndex{2}$: Results for $h=0.1$. Upper panels: graphical solution to self-consistency equation $m=\tanh\!\big((m+h)/\theta\big)$ at temperatures $\theta=0.65$ (blue), $\theta=0.9$ (dark green), and $\theta=1.5$ (dark red). Lower panel: mean field free energy, with energy shifted by $\theta\ln 2$ so that $f(m=0,\theta)=0$.

$h\ne 0$

Consider without loss of generality the case $h>0$. The minimum of the free energy $f(m,h,\theta)$ now lies at $m>0$ for any $\theta$. At low temperatures, the double well structure we found in the $h=0$ case is tilted so that the right well lies lower in energy than the left well. This is depicted in Figure $\PageIndex{2}$. As the temperature is raised, the local minimum at $m<0$ vanishes, annihilating with the local maximum in a saddle-node bifurcation. To find where this happens, one sets ${\pz f\over\pz m}=0$ and ${\pz^2\!f\over\pz m^2}=0$ simultaneously, resulting in

$$h^*(\theta)=\sqrt{1-\theta}-{\theta\over 2}\ln\!\bigg({1+\sqrt{1-\theta}\over 1-\sqrt{1-\theta}}\bigg) . \label{IMFhstar}$$

The solutions lie at $h=\pm h^*(\theta)$. For $\theta<\theta\ns_\Rc=1$ and $h\in \big[\!-\!h^*(\theta)\,,\,+h^*(\theta)\big]$, there are three solutions to the mean field equation. Equivalently we could in principle invert the above expression to obtain $\theta^*(h)$. For $\theta>\theta^*(h)$, there is only a single global minimum in the free energy $f(m)$ and there is no local minimum. Note $\theta^*(h=0)=1$.

Assuming $h\ll |\theta-1|\ll 1$, the mean field solution for $m(\theta,h)$ will also be small, and we expand the free energy in $m$, and to linear order in $h$:

$$\begin{split} f(m,h,\theta)&=-\theta\,\ln 2 + \half (1-\theta^{-1})\, m^2 + {m^4\over 12\, \theta^3} - {hm\over \theta}\\ &=f\nd_0 + \half\, (\theta-1)\,m^2 + \frac{1}{12} m^4 - hm + \ldots \ . \end{split}$$

Setting $\frac{\pz f}{\pz m}=0$, we obtain

$$\frac{1}{3} m^3 + (\theta-1)\cdot m - h =0\ . \label{IMFmheqn}$$

If $\theta>1$ then we have a solution $m=h/(\theta-1)$. The $m^3$ term can be ignored because it is higher order in $h$, and we have assumed $h\ll |\theta-1|\ll 1$. This is known as the Curie-Weiss law¹⁰. The magnetic susceptibility behaves as

$$\xhi(\theta)={\pz m\over\pz h}={1\over \theta-1} \propto |\theta-1|^{-\gamma}\ ,$$

where the magnetization critical exponent $\gamma$ is $\gamma=1$. If $\theta<1$ then while there is still a solution at $m=h/(\theta-1)$, it lies at a local maximum of the free energy, as shown in Figure $\PageIndex{2}$. The minimum of the free energy occurs close to the $h=0$ solution $m=m\ns_0(\theta)\equiv \sqrt{3}\,(1-\theta)$, and writing $m=m\ns_0+\delta m$ we find $\delta m$ to linear order in $h$ as $\delta m(\theta,h)=h/2(1-\theta)$. Thus,

$$m(\theta,h)=\sqrt{3}\,(1-\theta)^{1/2} +{h\over 2(1-\theta)}\ .$$

Once again, we find that $\xhi(\theta)$ diverges as $|\theta-1|^{-\gamma}$ with $\gamma=1$. The exponent $\gamma$ on either side of the transition is the same.

Finally, we can set $\theta=\theta\ns_\Rc$ and examine $m(h)$. We find, from Equation $\ref{IMFmheqn}$,

$$m(\theta=\theta\ns_\Rc,h)=(3h)^{1/3}\propto h^{1/\delta}\ ,$$

where $\delta$ is a new critical exponent. Mean field theory gives $\delta=3$. Note that at $\theta=\theta\ns_\Rc=1$ we have $m=\tanh(m+h)$, and inverting we find

$$h(m,\theta=\theta\ns_\Rc)=\half\ln\!\bigg({1+m\over 1-m}\bigg)-m={m^3\over 3} + {m^5\over 5} + \ldots \ ,$$

which is consistent with what we just found for $m(h,\theta=\theta\ns_\Rc)$.

Table $\PageIndex{1}$: Critical exponents from mean field theory as compared with exact results for the two-dimensional Ising model, numerical results for the three-dimensional Ising model, and experiments on the liquid-gas transition in CO${}_2$. Source: H. E. Stanley, Phase Transitions and Critical Phenomena.

		2D Ising	3D Ising	CO${}_2$
Exponent	MFT	(exact)	(numerical)	(expt.)
$\alpha$	$0$	$0$	$0.125$	$0.1$
$\beta$	$1/2$	$1/8$	$0.313$	$0.35$
$\gamma$	$1$	$7/4$	$1.25$	$1.26$
$\delta$	$3$	$15$	$5$	$4.2$

How well does mean field theory do in describing the phase transition of the Ising model? In table $\PageIndex{1}$ we compare our mean field results for the exponents $\alpha$, $\beta$, $\gamma$, and $\delta$ with exact values for the two-dimensional Ising model, numerical work on the three-dimensional Ising model, and experiments on the liquid-gas transition in CO${}_2$. The first thing to note is that the exponents are dependent on the dimension of space, and this is something that mean field theory completely misses. In fact, it turns out that the mean field exponents are exact provided $d>d\ns_\Ru$, where $d\ns_\Ru$ is the upper critical dimension of the theory. For the Ising model, $d\ns_\Ru=4$, and above four dimensions (which is of course unphysical) the mean field exponents are in fact exact. We see that all in all the MFT results compare better with the three dimensional exponent values than with the two-dimensional ones – this makes sense since MFT does better in higher dimensions. The reason for this is that higher dimensions means more nearest neighbors, which has the effect of reducing the relative importance of the fluctuations we neglected to include.

Magnetization dynamics

Dissipative processes drive physical systems to minimum energy states. We can crudely model the dissipative dynamics of a magnet by writing the phenomenological equation

$${dm\over ds}=-{\pz f\over\pz m}\ , \label{IMFmdyn}$$

where $s$ is a dimensionless time variable. Under these dynamics, the free energy is never increasing:

$${df\over ds}={\pz f\over\pz m}\,{\pz m\over\pz s}=-\bigg({\pz f\over\pz m}\bigg)^{\!2}\le 0\ .$$

Clearly the fixed point of these dynamics, where ${\dot m}=0$, is a solution to the mean field equation ${\pz f\over\pz m}=0$.

Figure $\PageIndex{3}$: Dissipative magnetization dynamics ${\dot m}=-f'(m)$. Bottom panel shows $h^*(\theta)$ from Equation $\ref{IMFhstar}$. For $(\theta,h)$ within the blue shaded region, the free energy $f(m)$ has a global minimum plus a local minimum and a local maximum. Otherwise $f(m)$ has only a single global minimum. Top panels show an imperfect bifurcation in the magnetization dynamics at $h=0.0215$ , for which $\theta^*=0.90$. Temperatures shown: $\theta=0.65$ (blue), $\theta=\theta^*(h)=0.90$ (green), and $\theta=1.2$. The rightmost stable fixed point corresponds to the global minimum of the free energy. The bottom of the middle two upper panels shows $h=0$, where both of the attractive fixed points and the repulsive fixed point coalesce into a single attractive fixed point (supercritical pitchfork bifurcation).

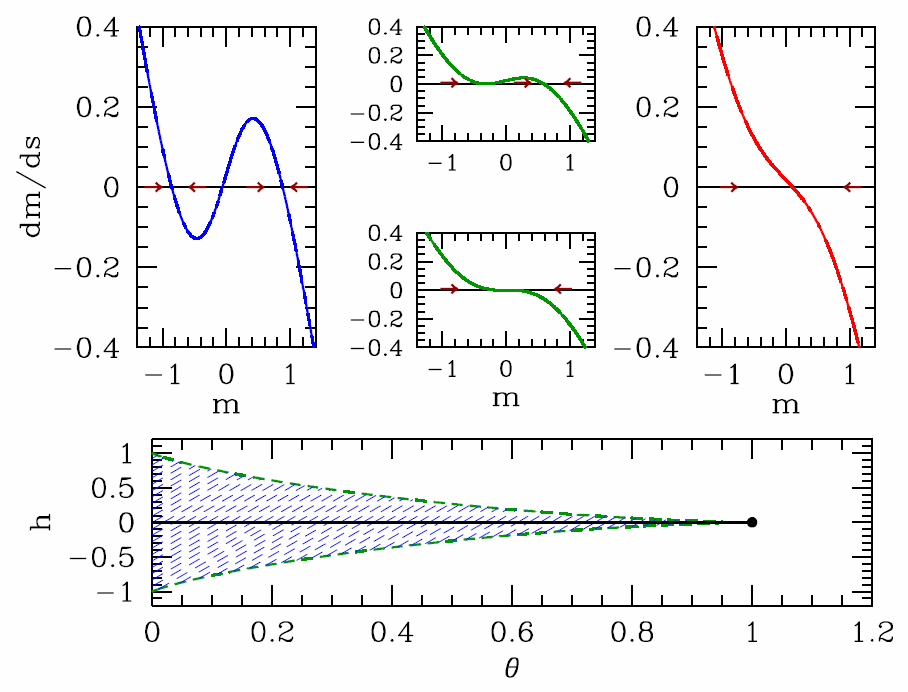
The phase flow for the equation ${\dot m}=-f'(m)$ is shown in Figure $\PageIndex{3}$. As we have seen, for any value of $h$ there is a temperature $\theta^*$ below which the free energy $f(m)$ has two local minima and one local maximum. When $h=0$ the minima are degenerate, but at finite $h$ one of the minima is a global minimum. Thus, for $\theta<\theta^*(h)$ there are three solutions to the mean field equations. In the language of dynamical systems, under the dynamics of Equation $\ref{IMFmdyn}$, minima of $f(m)$ correspond to attractive fixed points and maxima to repulsive fixed points. If $h>0$, the rightmost of these fixed points corresponds to the global minimum of the free energy. As $\theta$ is increased, this fixed point evolves smoothly. At $\theta=\theta^*$, the (metastable) local minimum and the local maximum coalesce and annihilate in a saddle-note bifurcation. However at $h=0$ all three fixed points coalesce at $\theta=\theta\ns_\Rc$ and the bifurcation is a supercritical pitchfork. As a function of $t$ at finite $h$, the dynamics are said to exhibit an imperfect bifurcation, which is a deformed supercritical pitchfork.

Figure $\PageIndex{4}$: Top panel : hysteresis as a function of ramping the dimensionless magnetic field $h$ at $\theta=0.40$. Dark red arrows below the curve follow evolution of the magnetization on slow increase of $h$. Dark grey arrows above the curve follow evolution of the magnetization on slow decrease of $h$. Bottom panel : solution set for $m(\theta,h)$ as a function of $h$ at temperatures $\theta=0.40$ (blue), $\theta=\theta_\Rc=1.0$ (dark green), and $t=1.25$ (red).

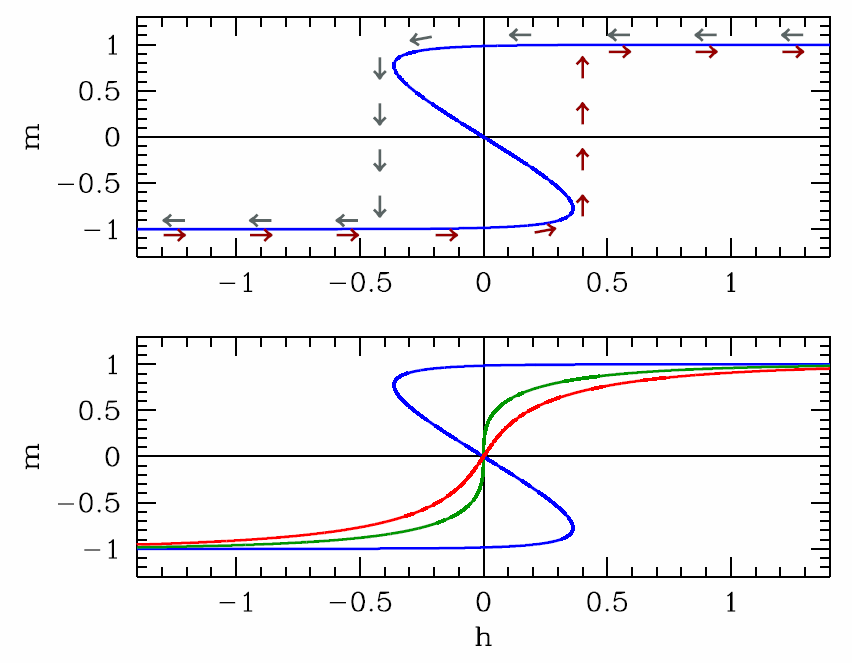
The solution set for the mean field equation is simply expressed by inverting the $\tanh$ function to obtain $h(\theta,m)$. One readily finds

$$h(\theta,m)={\theta\over 2}\,\ln\!\bigg({1+m\over 1-m}\bigg)-m\ .$$

As we see in the bottom panel of Figure $\PageIndex{4}$, $m(h)$ becomes multivalued for $h\in\big[-h^*(\theta)\,,\,+h^*(\theta)\big]$, where $h^*(\theta)$ is given in Equation $\ref{IMFhstar}$. Now imagine that $\theta<\theta\ns_\Rc$ and we slowly ramp the field $h$ from a large negative value to a large positive value, and then slowly back down to its original value. On the time scale of the magnetization dynamics, we can regard $h(s)$ as a constant. (Remember the time variable is $s$ here.) Thus, $m(s)$ will flow to the nearest stable fixed point. Initially the system starts with $m=-1$ and $h$ large and negative, and there is only one fixed point, at $m^*\approx -1$. As $h$ slowly increases, the fixed point value $m^*$ also slowly increases. As $h$ exceeds $-h^*(\theta)$, a saddle-node bifurcation occurs, and two new fixed points are created at positive $m$, one stable and one unstable. The global minimum of the free energy still lies at the fixed point with $m^*<0$. However, when $h$ crosses $h=0$, the global minimum of the free energy lies at the most positive fixed point $m^*$. The dynamics, however, keep the system stuck in what is a metastable phase. This persists until $h=+h^*(\theta)$, at which point another saddle-note bifurcation occurs, and the attractive fixed point at $m^*<0$ annihilates with the repulsive fixed point. The dynamics then act quickly to drive $m$ to the only remaining fixed point. This process is depicted in the top panel of Figure $\PageIndex{4}$. As one can see from the figure, the the system follows a stable fixed point until the fixed point disappears, even though that fixed point may not always correspond to a global minimum of the free energy. The resulting $m(h)$ curve is then not reversible as a function of time, and it possesses a characteristic shape known as a hysteresis loop. Etymologically, the word hysteresis derives from the Greek $\ups\sigma\tau\ve\rho\eta\sigma\iota\varsigma$, which means ‘lagging behind’. Systems which are hysteretic exhibit a history-dependence to their status, which is not uniquely determined by external conditions. Hysteresis may be exhibited with respect to changes in applied magnetic field, changes in temperature, or changes in other externally determined parameters.

Beyond nearest neighbors

Suppose we had started with the more general model,

$$\begin{split} \HH&=-\sum_{i<j} J\ns_{ij}\,\sigma\ns_i\,\sigma\ns_j - H\sum_i\sigma\ns_i\\ &=-\half\sum_{i\ne j} J\ns_{ij}\,\sigma\ns_i\,\sigma\ns_j - H\sum_i\sigma\ns_i\ , \end{split}$$

where $J_{ij}$ is the coupling between spins on sites $i$ and $j$. In the top equation above, each pair $(ij)$ is counted once in the interaction term; this may be replaced by a sum over all $i$ and $j$ if we include a factor of $\half$.¹¹ The resulting mean field Hamiltonian is then

$$\HH\ns_{\ssr{MF}}=\half N\jhz\,m^2- \big(H+\jhz\,m\big)\sum_i\sigma_i\ .$$

Here, ${\hat J}(\Bq)$ is the Fourier transform of the interaction matrix $J\ns_{ij}$:¹²

$${\hat J}(\Bq)=\sum_\BR J(\BR)\,e^{-i\Bq\cdot\BR}\ .$$

For nearest neighbor interactions only, one has $\jhz=zJ$, where $z$ is the lattice coordination number, the number of nearest neighbors of any given site. The scaled free energy is as in Equation $\ref{fergsca}$, with $f=F/N\jhz$, $\theta=\kT/\jhz$, and $h=H/\jhz$. The analysis proceeds precisely as before, and we conclude $\theta\ns_\Rc=1$, $\kB T^{\ssr{MF}}_\Rc=\jhz$.

Ising model with long-ranged forces

Consider an Ising model where $J\ns_{ij}=J/N$ for all $i$ and $j$, so that there is a very weak interaction between every pair of spins. The Hamiltonian is then

$$\HH=-{J\over 2N}\bigg(\sum_i\sigma\ns_i\bigg)^{\!2} - H\sum_k\sigma\ns_k\ .$$

The partition function is

$$Z= \Tra_{\{\sigma_i\}}\,\exp\!\Bigg[ {\beta J\over 2N}\bigg(\sum_i\sigma\ns_i\bigg)^{\!2} + \beta H\sum_i\sigma\ns_i\Bigg]\ .$$

We now invoke the Gaussian integral,

$$\int\limits_{-\infty}^\infty\!\!\!dx\>e^{-\alpha x^2 - \beta x}=\sqrt{\pi\over\alpha\,}\>e^{\beta^2/4\alpha}\ .$$

Thus,

$$\exp\!\Bigg[ {\beta J\over 2N}\bigg(\sum_i\sigma\ns_i\bigg)^{\!2}\Bigg]=\bigg({N\beta J\over 2\pi}\bigg)^{\!\!1/2}\! \int\limits_{-\infty}^\infty\!\!\!dm\>e^{-{1\over 2} N\beta J m^2 + \beta J m\sum_i\sigma\ns_i}\ ,$$

and we can write the partition function as

$$\begin{split} Z&=\bigg({N\beta J\over 2\pi }\bigg)^{\!\!1/2}\!\int\limits_{-\infty}^\infty\!\!\!dm\>e^{-{1\over 2} N\beta J m^2} \bigg(\sum_\sigma e^{\beta(H+Jm)\sigma}\bigg)^{\!N}\\ &=\bigg({N\over 2\pi \theta}\bigg)^{\!\!1/2}\!\int\limits_{-\infty}^\infty\!\!\!dm\>e^{-N A(m)/\theta}\ , \end{split}$$

where $\theta=\kT/J$, $h=H/J$, and

$$A(m)=\half m^2-\theta\ln\! \left[2\cosh \bigg({h+m\over\theta}\bigg)\right]\ .$$

Since $N\to\infty$, we can perform the integral using the method of steepest descents. Thus, we must set

$${dA\over dm}\bigg|\nd_{m^*}=0 \quad\Longrightarrow\quad m^*=\tanh\bigg({m^*+h\over\theta}\bigg)\ .$$

Expanding about $m=m^*$, we write

$$A(m)=A(m^*) + \half A''(m^*)\,(m-m^*)^2 + \frac{1}{6}\,A'''(m^*)\,(m-m^*)^3 + \ldots\ .$$

Performing the integrations, we obtain

$$\begin{split} Z&=\bigg({N\over 2\pi\theta}\bigg)^{1/2} e^{-NA(m^*)/\theta}\!\!\int\limits_{-\infty}^\infty\!\!\!d\nu\> \exp\!\Bigg[-{N A''(m^*)\over 2\theta}\>m^2 - {NA'''(m^*)\over 6\theta}\>m^3 + \ldots\Bigg]\\ &={1\over\sqrt{A''(m^*)}}\>e^{-NA(m^*)/\theta}\cdot\Big\{ 1 + \CO(N^{-1})\Big\}\ . \end{split}$$

The corresponding free energy per site

$$f={F\over NJ}=A(m^*)+{\theta\over 2N}\,\ln A''(m^*) + \CO(N^{-2})\ ,$$

where $m^*$ is the solution to the mean field equation which minimizes $A(m)$. Mean field theory is exact for this model!