18.8: Coefficient of Expansion
( \newcommand{\kernel}{\mathrm{null}\,}\)
If a specimen can be obtained in the form of a long rod, the simplest and most direct method is merely to rest the rod horizontally on some support, immersed in a water bath by which means the temperature can be varied. Two scratches, one at each end of the rod, can be observed with a pair of measuring microscopes held on a support at constant temperature. The measuring microscopes can either be fixed and fitted with a fine scale in the eyepiece of each, or they may be movable by means of a fine precision screw (96 turns to the inch). The movement of the microscopes can be measured either by means of a wheel fitted with a vernier that turns the precision screw, or by attaching a corner reflector to each moving microscope, and reflecting a laser beam off the reflector and counting the number of half wavelengths traversed by the microscope.
If the specimen cannot be obtained in the form of a long rod, but can be obtained in the form of a thin, flat plate with parallel faces, another method can be used. A hole might be cut in the flat specimen, and the specimen can be rested on top of a flat glass plate. A second flat glass plate rests on the upper face of the specimen. The arrangement can be illuminated with an extended monochromatic light source, to create a system of interference fringes. When the temperature is raised, the specimen expands and the distance between the glass plates increases by an amount that can be measured by measuring the movement of the interference fringes. Some materials may not be easily obtainable either in the form of a long rod or a thin plate, but perhaps they can be obtained in the form of a small cube. The specimen is placed side-by-side with a similar cube of quartz, whose expansion coefficient is very small, the two resting on the horizontal surface of a polished shiny metal or glass block. On top of the two specimens rests a thin, flat glass plate. A narrow beam of light, preferably from a laser, is directed from above to the arrangement, and two reflections are observed, one from the thin glass plate that rests on top of the specimen and its quartz companion, the other from the upper surface of the block on which the specimens are resting. When the specimen and the quartz are warmed, the specimen expands more than the quartz does, and so the upper thin glass plate tilts, and the reflection from it is deflected. The displacement of one reflected beam from the other can be measured with a microscope, and hence the tilt of the upper glass plate can be calculated, and hence the excess of expansion of the specimen over that of the quartz can be determined. The experiment gives the difference in expansion coefficient between the specimen and the quartz. The latter is very small, and its exact value need not be known with great precision in order to obtain the absolute coefficient of expansion of the specimen.
For nonvolatile liquids, a weight thermometer can be used. This is a glass (or, better, fused quartz) bulb fitted with a narrow capillary tube as shown in figure XVIII.3.
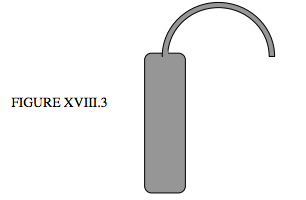
The bulb (whose weight empty is known) is completely filled (including the capillary to the very tip) with the liquid, and weighed, so that the weight, hence mass, of the liquid is known. The temperature is increased, so some liquid escapes, and the bulb is weighed again. Thus we know the weight of the liquid held by the bulb at two temperatures. If we assume that the volume is constant (the bulb being made of fused quartz) this enables us to calculate the coefficient of expansion of the liquid. Of course, the bulb does expand a little, so what we have determined is the difference between the volume expansions of the liquid and the quartz. If we know the volume expansion of the quartz (which need not be known to high precision, since it is small), we can then determine the absolute coefficient of expansion of the liquid.
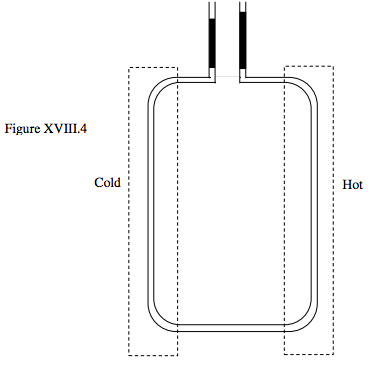
In another method for measuring the coefficient of expansion of liquids, the liquid is contained in a U-tube, the two arms of which are maintained at different temperatures, as shown in figure XVIII.4. The upper ends of the two arms of the U-tube are connected to vertical tubes containing mercury for controlling and measuring the pressure. The apparatus is maintained so that the volumes of the liquids in the two arms of the U-tube are equal – but because the two arms are at different temperatures, their densities (hence specific volumes) are different, so a little extra mercury is needed to balance the hot arm against the cold arm. Thus it is possible to determine the difference in densities at the two temperatures, and hence to determine the volume coefficient of expansion. The figure shows the principle of the method; some practical refinements are needed in the actual equipment.