14.5: Energy Transported by a Wave
- Page ID
- 19465
In this section, we examine how to model the energy that is transported by waves. Although no material moves along with a wave, mechanical energy can be transported by a wave, as evidenced by the damage caused by the waves from an earthquake.
A wave as being made of simple harmonic oscillators
Consider a wave that is propagating through a medium. We can model the motion of one of the particles in the medium as if it were the motion of a simple harmonic oscillator1. This is illustrated in Figure \(\PageIndex{1}\), which shows the displacement as a function of time for a point in the medium located at the origin when a wave passes through that point. The displacement of that point, at \(x=0\), if we choose \(\phi=0\), is given by:
\[\begin{aligned} D(x=0,t) = A\sin(-\omega t)\end{aligned}\]
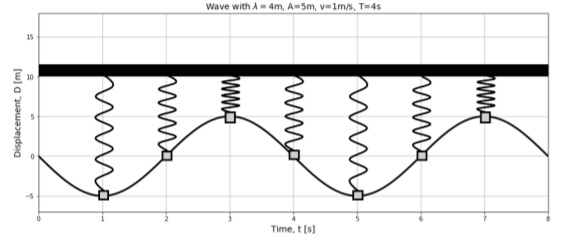
The displacement of the particle in the medium is described by the same equation as the position of a simple harmonic oscillator, with the same angular frequency \(\omega\), as that of the wave.
We can also view a snapshot of the wave in time, and model the different points in the medium as different oscillators that all have different displacements. This is shown in Figure \(\PageIndex{2}\).
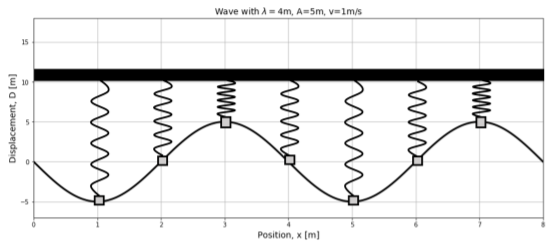
Energy transported in a one dimensional wave
In this section, we show how to describe the energy transported by a one-dimensional wave along a rope. We model each particle in the rope through which the wave propagates as a small simple harmonic oscillator with mass \(m\), attached to a spring with an effective spring constant, \(k_s\)2.
Of course, there is no actual spring, but we can still determine an effective spring constant, \(k_s\), from the angular frequency: \[\begin{aligned} \omega &= \sqrt{\frac{k_s}{m}}\\ \therefore k_s &= \omega^2 m\end{aligned}\] which corresponds to the spring constant that would give the correct angular frequency for the particle of mass \(m\).
The total mechanical energy of one oscillator, \(E_m\), can be evaluated when the oscillator is at its maximal displacement, \(A\), from its equilibrium, where its kinetic energy is zero: \[\begin{aligned} E_m = \frac{1}{2}k_s A^2 = \frac{1}{2}\omega^2 m A^2\end{aligned}\]
If the rope is infinitely long, and carries a continuous wave, it will have an infinite amount of energy, as it will correspond to an infinite number of oscillators. Instead, let us calculate how much energy, \(E_\lambda\), is stored in the wave over one wavelength, \(\lambda\). To do so, we need to evaluate how many effective oscillators are contained in the rope, over a distance \(\lambda\), so that we can sum all of their energies together to obtain the energy stored in one wavelength: \[\begin{aligned} E_\lambda = \sum \frac{1}{2}\omega^2 m A^2\end{aligned}\] where the sum is over the number of oscillators in one wavelength. Of course, the rope is not actually made of oscillators, but we can model each section of rope of length \(dx\) has being an oscillator of mass \(dm=\mu dx\), where \(\mu\) is the linear mass density of the rope. The sum (integral) of the energy of the oscillators over one wavelength can thus be written as: \[\begin{aligned} E_\lambda = \int_0^\lambda \frac{1}{2}\omega^2 \mu A^2 dx = \frac{1}{2}\omega^2 \mu A^2 \lambda\end{aligned}\] The energy stored in one wavelength is not a very useful property of a wave, since the total energy in the wave depends on the length of the wave. We can describe the rate at which energy is transmitted by the wave (its power), since we know how long, \(T\), it will take the wave to travel one wavelength, and we just determined how much energy is stored in one wavelength. The average power with which energy is transported by a wave is given by: \[\begin{aligned} P = \frac{E_\lambda}{T} = \frac{\frac{1}{2}\omega^2 \mu A^2 \lambda}{T}=\frac{1}{2}\omega^2 \mu A^2 v\end{aligned}\] where \(T\) is the period of the wave, and \(v=\lambda/T\) is the speed of the wave. The power transmitted by a wave on a rope is thus given by:
\[P=\frac{1}{2}\omega ^{2}\mu A^{2}v\]
We can see that the power transmitted by a wave goes as the amplitude, \(A\), of the wave squared. It thus takes four times more energy to double the amplitude of waves that are sent down a rope.
Energy transported in a spherical, three-dimensional, wave
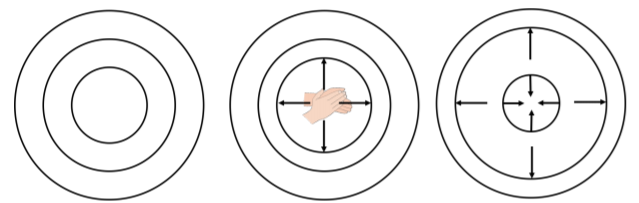
In this section, we show how to model the rate at which energy is transported in spherical three-dimensional waves, such as the sound waves that are generated when you clap your hands. A spherical sound wave is a pressure disturbance in the air that propagates spherically outwards from a point of emission. We can think of thin spherical shells containing air that expand and contract about their equilibrium position as the wave moves through the shells. The motion of each shell is similar to that of a simple harmonic oscillator of mass \(dm\), where \(dm\) is the mass of air in the oscillating shell.
Consider a shell at a radial position, \(r\), from the source, with thickness \(dr\), and mass \(dm\):
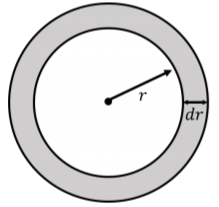
If the medium has a density, \(\rho\), then the mass of the shell is given by: \[\begin{aligned} dm = \rho dV = \rho 4\pi r^2 dr\end{aligned}\] where \(dV = 4\pi r^2 dr\) is the volume of the shell. Again, if we model each shell as a simple harmonic oscillator with mass \(dm\), then the energy, \(dE\), stored in that oscillating shell is given by: \[\begin{aligned} dE = \frac{1}{2}k_s A^2 = \frac{1}{2}\omega^2 dm A^2 = \frac{1}{2}\omega^2 A^2 \rho 4\pi r^2 dr=2\pi\rho \omega^2 A^2 r^2 dr\end{aligned}\] where \(\omega\) is the angular frequency of the wave, and \(A\) is the amplitude of the wave. We expressed the effective spring constant, \(k_s\), in terms of the angular frequency of the simple harmonic oscillator and its mass, as we did in the previous section. It now makes less sense to determine the energy that is stored in one wavelength of the wave because the energy, \(dE\), stored in one shell depends on the location, \(r\), of that shell. This was not the case for a one-dimensional wave, where the energy stored in one oscillator did not depend on the position of that oscillator.
The rate at which energy is transported by the wave is given by: \[\begin{aligned} P = \frac{dE}{dt}\end{aligned}\] We can use the Chain Rule to change this into a derivative over \(r\): \[\begin{aligned} P = \frac{dE}{dr}\frac{dr}{dt}=\frac{dE}{dr}v\end{aligned}\] where \(\frac{dr}{dt}=v\) is the speed of the wave (the rate of change of the radius of a shell). The power transmitted by the spherical wave is thus given by: \[\begin{aligned} P &=\frac{dE}{dr}v =2\pi\rho \omega^2 A^2 r^2 v\end{aligned}\] where the power appears to depends on how far you are from the source (\(r\)).
Suppose that you have a \(50\text{W}\) speaker emitting sound; each radial shell emanating from the speaker must transport energy at a rate of \(50\text{W}\). This is simply a statement that the energy radiated by the speaker has to move from one shell to the next and be conserved. Since the power transported by a shell appears to depend on the radius of the shell, if the power transmitted by each shell is the same, then the amplitude of the wave in each shell must decrease, so that the power does not actually depend on the radius of the shell. In particular, for a spherical wave, the amplitude will decrease as a function of distance from the source: \[\begin{aligned} P& = \text{constant}\\ \therefore A&=\frac{1}{r}\sqrt{\frac{P}{2\pi\rho \omega^2 v}}\end{aligned}\] This is very different from the propagation of a one-dimensional wave, in which the amplitude does not change with distance. In practice, if there are energy losses due to, say, friction, then the amplitude of a one-dimensional wave would also decrease with distance from the source, but this is a different effect.
Olivia's Thoughts
Here’s a slightly different way to think about why the amplitude of the wave decreases as you get further from the source. When a spherical wave travels outwards, energy is passed from one shell to the next. The outer shells are bigger than the inner shells, and so they will contain more particles. Because of conservation of energy, when the energy is transferred from one shell to the next, the total energy stays the same. In the outer shells, the energy must be shared between a greater number of particles, so each particle gets less energy, and therefore oscillates with a smaller amplitude than the particles in the previous shell did.
To remember this, imagine the shells in Figure \(\PageIndex{3}\) are circles of kids standing side by side. The innermost circle has \(10\) kids and the outermost circle has \(100\) kids. If you have \(100\) candies, and you give them to the kids in the innermost circle, each will get \(10\) so they will get really hyper and start jumping around a lot. If you instead give the \(100\) candies to the kids in the outermost circle, each will only get one. The kids will only get a little bit hyper and jump around less.
The “intensity of a wave”, \(I\), is defined as the power per unit area that is transmitted by the wave. For a spherical wave front at radial position \(r\), with area \(4\pi r^2\), the intensity of the wave is defined as: \[\begin{aligned} I = \frac{P}{4\pi r^2} = \frac{1}{2}\rho \omega^2 A^2 v\end{aligned}\]
Usually, the intensity of a wave is something that you can measure, as it corresponds to the power delivered into some measuring device with a known surface area. For example, we cannot directly measure the total power that is transported by the waves from an earthquake, as we would need an instrument that could encompass the entire resulting wave. Instead, we can measure the intensity of waves from the earthquake by measuring how much power is delivered into some instrument with a known surface area. By knowing our distance from the earthquake, we could then determine the total power output of the earthquake.
The intensity is a measure of how much energy is delivered per unit area by a wave and goes down as the square of the distance from the source (since \(A\propto 1/r\)). If the source of the wave is an earthquake, then your house will have four times less damage than your friend’s, if your house is located only twice as far from the epicenter as your friend’s. You will cause four times less damage to your ears if you move only twice as far away from the stage at a rock concert.