14.6: Superposition of waves and interference
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we consider what happens when two (or more) different waves propagate in a medium and interfere with each other. The superposition principle states that if D1(x,t), D2(x,t), etc, are functions that satisfy the wave equation, then any linear combination of these functions, D(x,t):
D(x,t)=a1D1(x,t)+a2D2(x,t)+a3D3(x,t)+…
will also satisfy the wave equation.
Suppose that you hold one end of a rope and shake it with a specific frequency, creating waves that are described by:
D1(x,t)=A1sin(k1x−ω1t+ϕ1)
Your friend, at the other end of the rope shakes the rope with a different frequency, creating waves that propagate in the opposite direction and that are described by:
D2(x,t)=A2sin(k2x+ω2t+ϕ2)
The superposition principle states that the net displacement at any position x at some time t can be found by summing the displacement from the two waves together:
D(x,t)=A1sin(k1x−ω1t+ϕ1)+A2sin(k2x+ω2t+ϕ2)
The superposition of waves is illustrated in Figure 14.6.1, which shows three waves, and their resulting sum in the bottom most panel.
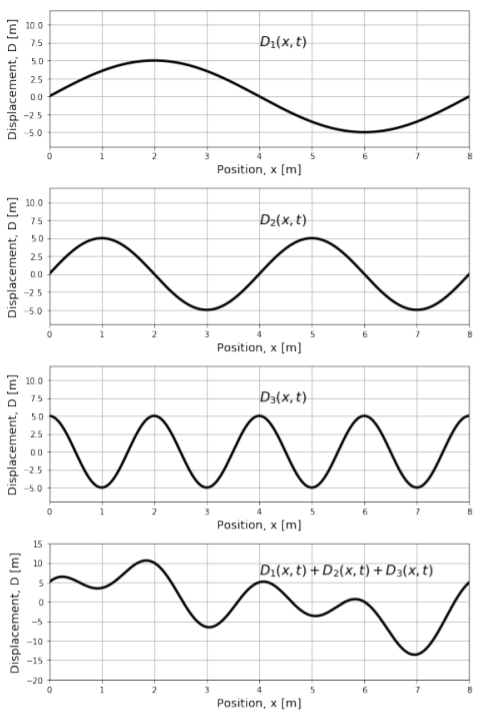
The resulting wave is created by the “interference” of the three waves, and mathematically is simply a sum of the three individual waves at each position (and instant in time). The resulting wave in this example has a rather complicated shape, that is no longer described by a sine function. However, by the superposition principle, it is a valid solution to the wave equation1.
The individual waves in the top three panels of Figure 14.6.1 all have an amplitude of 5m. The resulting wave, at some points (e.g. at x=2m), has an amplitude that is larger than any of the individual waves; we say that, at those positions, the individual waves have “constructively interfered”. In other locations (e.g. at x=6m), the resulting wave has a smaller amplitude than the individual waves, and we say that the individual waves have “destructively interfered”. The interference between waves can be observed easily on a water surface, for example by observing the constructive and destructive interference pattern of waves that originate from two pebbles being dropped at the same time a certain distance apart. Constructive interference between waves is also thought to be behind some reports of gigantic waves observed out at sea.
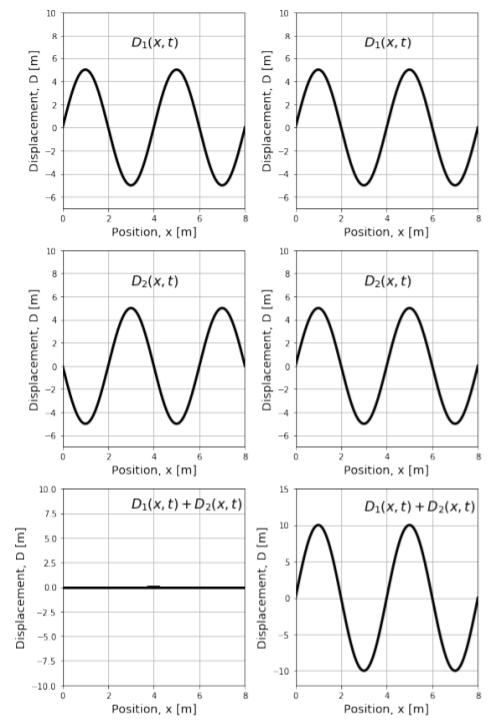
If two waves have the same wavelength and amplitude, it is possible for them to completely destructively interfere, resulting in no net wave. Similarly, they can also completely constructively interfere, resulting in a wave with a larger amplitude. Complete destructive and constructive interference are illustrated in the left and right panel of Figure 14.6.2, respectively.
Footnotes
1. Fourier’s Theorem states that any periodic function can be described as the linear combination of sine (or cosine) functions. This is the reason why we focused on using a sine function to describe a wave.

