14.10: Sample problems and solutions
( \newcommand{\kernel}{\mathrm{null}\,}\)
A clarinet can be modeled as an air column that is open at one end and closed at the other end, as in Figure 14.10.1.
- Draw the first three harmonics for a clarinet (draw the maximum displacement of the air molecules as a function of distance in the clarinet).
- Find an expression for the wavelength of the nth harmonic for a clarinet of length L.
- If a clarinet is 60cm long, what is the lowest frequency note it can produce?
- Answer
-
a. The first three harmonics are are shown in Figure 14.10.2.
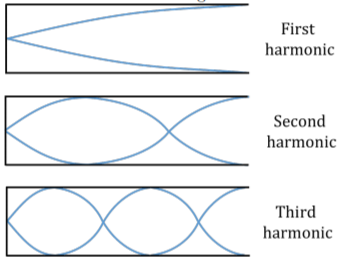
Figure 14.10.2: The first three harmonics for a clarinet. There is a node at the fixed end and an anti-node at the free end. b. The equation for a standing wave is:
D(x,t)=2Asin(kx)cos(ωt)
We let the fixed end be at x=0. At the fixed end, the displacement is equal to zero. At the free end (x=L) the displacement is maximized. The first condition is always true. The second condition will be met when:
sin(kL)=1∴kL=π/2,3π/2,...
This condition can be expressed as:
kL=(2n−1)π22πLλ=(2n−1)π2∴λ=4L2n−1
where, in the second line, we used k=2π/λ. We can check that this formula works for the first three harmonics:
n=1:λ=4L2(1)−1L=14λn=2:λ=4L2(2)−1L=34λn=3:λ=4L2(3)−1L=54λ
Referring back to our diagram (Figure 14.10.2), we can see that our formula holds true for the first three harmonics (i.e. for the first harmonic, the length of the clarinet is equal to 1/4 of a wavelength, etc.)
c. We found that the wavelength for the nth wavelength is given by:
λ=4L2n−1
Writing λ in terms of the velocity, v, and frequency, f, gives:
vf=4L2n−1∴f=v(2n−1)4L
From this formula, we can see that, if we want to find the lowest frequency, we want n=1. The length of the clarinet is 0.6m, and v is the speed of sound in air which is 343m/s at room temperature. Using these values, the lowest frequency is:
f=(343m/s)(2(1)−1)4(0.6m)f=143Hz
Discussion: This frequency is close to the D3 note, which has a frequency of 144Hz, so this answer makes sense. However, the value we found differs from the true value. Why might this be?
A pulse propagates down a rope of mass per unit length μ1 that is tied to a second rope with a mass per unit length μ2 (Figure 14.10.3). The tensions in the ropes are equal in magnitude.
- Write the displacements of the incident pulse, the reflected pulse, and the transmitted pulse in the form D(x,t)=D(a(t±x/v)), where a is some constant that you need to determine, and the choice of + or − depends on the direction that the pulse is traveling in.
- The reflection coefficient, R, is the ratio of the amplitude of the reflected pulse to the amplitude of the incident pulse. Using the boundary conditions, show that the reflection coefficient is given by:
R=√μ1−√μ2√μ1+√μ2
Note: The boundary is the interface between the two ropes. By “using the boundary conditions”, we mean that you should think about what must be true at the boundary for this problem to make sense. Boundary conditions are often more obvious than you think!
- Answer
-
a. We let the incident pulse move in the positive x direction (Figure 14.10.4), and set x=0 to be where the ropes connect.
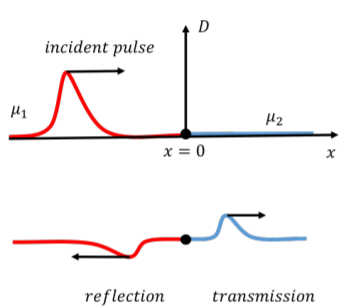
Figure 14.10.4: An incident pulse propagates through a rope connected to a another rope with a different linear mass density. When it reaches the boundary, part of the pulse is reflected and part is transmitted. Whether the reflected pulse is inverted or upright will depend on the reflection coefficient. The incident pulse (denoted by i) is a traveling wave, moving in one dimension in the positive x direction. The incident pulse can thus be described by the function:
DI(x,t)=AIcos(k1x−ωt)
We will use the formulas k=2π/λ and ω=2πf to rewrite this equation in the form D=(a(t±x/v)). The frequency, f, of the wave will be the same in both ropes. The velocity of the wave, and therefore its wavelength, depends on the mass density of the rope. Since the incident wave travels through the first rope (μ1), its velocity will be v1 and its wavelength will be λ1. The incident wave can thus be described by:
DI=AIcos(2πλ1x−2πft)=AIcos(2π(1λ1x−ft))=AIcos(2πf(xv1−t))=AIcos(−2πf(t−xv1))DI=AIcos(2πf(t−xv1))
where we used v=fλ, and noted that cos(−x)=cos(x).
The transmitted wave (denoted by the subscript T) will also travel in the positive x direction, but its speed will be v2, since it travels through the second rope:DT=ATcos(2πf(t−xv2))
The reflected wave (denoted by R) will travel in the −x direction and at the same speed as the incident pulse.
DR=ARcos(2πf(t+xv1))
b. We will consider the boundary conditions at the interface between the two ropes. One boundary condition is that the rope must be continuous. As a result, the vertical displacement on the −x side of the boundary must be the same as the vertical displacement on the +x side of the boundary at every instant:
D−x=D+xat x=0
The amplitude on the +x side is equal to the amplitude of the transmitted pulse. For the −x side of the boundary, we have to take into account that the incident and reflected pulses will superimpose (when the front of the incident pulse reaches the boundary, it will be reflected and interfere with the end of the incident pulse). This boundary condition can thus be expressed as:
AI+AR=AT
The slope of the rope must also be continuous at the boundary. Since the incident and reflected pulses superimpose, and the principle of superposition states that the net displacement is the sum of the displacement of these two waves, we can write:
∂∂x(DI+DR)|x=0=∂∂xDT|x=0∂∂xDI|x=0+∂∂xDR|x=0=∂∂xDT|x=0
Using our equations for the incident, transmitted, and reflected pulses found in part a), and taking the appropriate partial derivatives, this equation becomes:
(AI/v1)sin(2πf(t−xv1))|x=0+(−AR/v1)sin(2πf(t+xv1))|x=0=(AT/v2)sin(2πf(t−xv2))|x=0
Evaluating at x=0 gives:
(AI/v1)sin(2πft)+(−AR/v1)sin(2πft)=(AT/v2)sin(2πft)AIv1−ARv1=ATv2
Using our first condition, AI+AR=AT, we get:
AIv1−ARv1=AIv2+ARv2
Now, we can rearrange to find the reflection coefficient, R=AR/AI:
AI(v2−v1v1v2)=AR(v2+v1v1v2)R=v2−v1v2+v1
Since the velocities in the first and second rope are v1=√FT/μ1 and v2=√FT/μ2, respectively, the reflection coefficient can be written as:
R=√FTμ2−√FTμ1√FTμ2+√FTμ1=√FT√FT⋅1√μ2−1√μ11√μ2+1√μ1∴R=√μ1−√μ2√μ1+√μ2
as desired.

