9.9: Current and Resistance (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
9.2 Electrical Current
1. Can a wire carry a current and still be neutral—that is, have a total charge of zero? Explain.
2. Car batteries are rated in ampere-hours (A⋅h). To what physical quantity do ampere-hours correspond (voltage, current, charge, energy, power,…)?
3. When working with high-power electric circuits, it is advised that whenever possible, you work “one-handed” or “keep one hand in your pocket.” Why is this a sensible suggestion?
9.3 Model of Conduction in Metals
4. Incandescent light bulbs are being replaced with more efficient LED and CFL light bulbs. Is there any obvious evidence that incandescent light bulbs might not be that energy efficient? Is energy converted into anything but visible light?
5. It was stated that the motion of an electron appears nearly random when an electrical field is applied to the conductor. What makes the motion nearly random and differentiates it from the random motion of molecules in a gas?
6. Electric circuits are sometimes explained using a conceptual model of water flowing through a pipe. In this conceptual model, the voltage source is represented as a pump that pumps water through pipes and the pipes connect components in the circuit. Is a conceptual model of water flowing through a pipe an adequate representation of the circuit? How are electrons and wires similar to water molecules and pipes? How are they different?
7. An incandescent light bulb is partially evacuated. Why do you suppose that is?
9.4 Resistivity and Resistance
8. The IR drop across a resistor means that there is a change in potential or voltage across the resistor. Is there any change in current as it passes through a resistor? Explain.
9. Do impurities in semiconducting materials listed in Table 9.1 supply free charges? (Hint: Examine the range of resistivity for each and determine whether the pure semiconductor has the higher or lower conductivity.)
10. Does the resistance of an object depend on the path current takes through it? Consider, for example, a rectangular bar—is its resistance the same along its length as across its width?
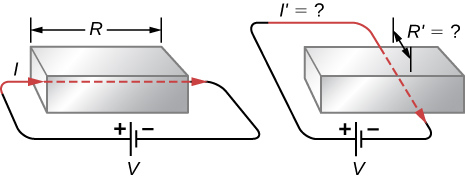
11. If aluminum and copper wires of the same length have the same resistance, which has the larger diameter? Why?
9.5 Ohm's Law
12. In Determining Field from Potential, resistance was defined as R≡VI. In this section, we presented Ohm’s law, which is commonly expressed as V=IR. The equations look exactly alike. What is the difference between Ohm’s law and the definition of resistance?
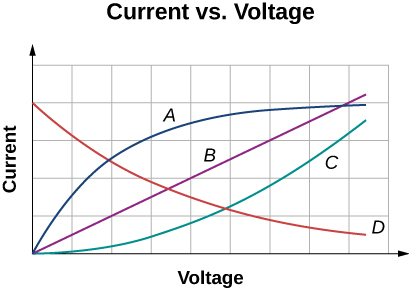
13. Shown below are the results of an experiment where four devices were connected across a variable voltage source. The voltage is increased and the current is measured. Which device, if any, is an ohmic device?
14. The current I is measured through a sample of an ohmic material as a voltage V is applied. (a) What is the current when the voltage is doubled to 2V (assume the change in temperature of the material is negligible)? (b) What is the voltage applied is the current measured is 0.2I (assume the change in temperature of the material is negligible)? What will happen to the current if the material if the voltage remains constant, but the temperature of the material increases significantly?
9.6 Electrical Energy and Power
15. Common household appliances are rated at 110 V, but power companies deliver voltage in the kilovolt range and then step the voltage down using transformers to 110 V to be used in homes. You will learn in later chapters that transformers consist of many turns of wire, which warm up as current flows through them, wasting some of the energy that is given off as heat. This sounds inefficient. Why do the power companies transport electric power using this method?
16. Your electric bill gives your consumption in units of kilowatt-hour (kW ⋅· h). Does this unit represent the amount of charge, current, voltage, power, or energy you buy?
17. Resistors are commonly rated at 18W,14W,12W, 1 W and 2 W for use in electrical circuits. If a current of I=2.00A is accidentally passed through a R=1.00Ω resistor rated at 1 W, what would be the most probable outcome? Is there anything that can be done to prevent such an accident?
18. An immersion heater is a small appliance used to heat a cup of water for tea by passing current through a resistor. If the voltage applied to the appliance is doubled, will the time required to heat the water change? By how much? Is this a good idea?
9.7 Superconductors
19. What requirement for superconductivity makes current superconducting devices expensive to operate?
20. Name two applications for superconductivity listed in this section and explain how superconductivity is used in the application. Can you think of a use for superconductivity that is not listed?
Problems
9.2 Electrical Current
21. A Van de Graaff generator is one of the original particle accelerators and can be used to accelerate charged particles like protons or electrons. You may have seen it used to make human hair stand on end or produce large sparks. One application of the Van de Graaff generator is to create X-rays by bombarding a hard metal target with the beam. Consider a beam of protons at 1.00 keV and a current of 5.00 mA produced by the generator.
(a) What is the speed of the protons?
(b) How many protons are produced each second?
22. A cathode ray tube (CRT) is a device that produces a focused beam of electrons in a vacuum. The electrons strike a phosphor-coated glass screen at the end of the tube, which produces a bright spot of light. The position of the bright spot of light on the screen can be adjusted by deflecting the electrons with electrical fields, magnetic fields, or both. Although the CRT tube was once commonly found in televisions, computer displays, and oscilloscopes, newer appliances use a liquid crystal display (LCD) or plasma screen. You still may come across a CRT in your study of science. Consider a CRT with an electron beam average current of 25.00μA25.00μA. How many electrons strike the screen every minute?
23. How many electrons flow through a point in a wire in 3.00 s if there is a constant current of I=4.00A?
24. A conductor carries a current that is decreasing exponentially with time. The current is modeled as I=I0e−t/τ, where I0=3.00A is the current at time t=0.00s and τ=0.50s is the time constant. How much charge flows through the conductor between t=0.00s and t=3τ?
25. The quantity of charge through a conductor is modeled as Q=4.00Cs4t4−1.00Cst+6.00mC. What is the current at time t=3.00s?
26. The current through a conductor is modeled as I(t)=Imsin(2π[60Hz]t). Write an equation for the charge as a function of time.
27. The charge on a capacitor in a circuit is modeled as Q(t)=Qmaxcos(ωt+ϕ). What is the current through the circuit as a function of time?
9.3 Model of Conduction in Metals
28. An aluminum wire 1.628 mm in diameter (14-gauge) carries a current of 3.00 amps.
(a) What is the absolute value of the charge density in the wire?
(b) What is the drift velocity of the electrons?
(c) What would be the drift velocity if the same gauge copper were used instead of aluminum? The density of copper is 8.96g/cm3 and the density of aluminum is 2.70g/cm3. The molar mass of aluminum is 26.98 g/mol and the molar mass of copper is 63.5 g/mol. Assume each atom of metal contributes one free electron.
29. The current of an electron beam has a measured current of I=50.00μA with a radius of 1.00 mm. What is the magnitude of the current density of the beam?
30. A high-energy proton accelerator produces a proton beam with a radius of r=0.90mm. The beam current is I=9.00μA and is constant. The charge density of the beam is n=6.00×1011 protons per cubic meter.
(a) What is the current density of the beam?
(b) What is the drift velocity of the beam?
(c) How much time does it take for 1.00×1010 protons to be emitted by the accelerator?
31. Consider a wire of a circular cross-section with a radius of R=3.00mm. The magnitude of the current density is modeled as J=cr2=5.00×106Am4r2. What is the current through the inner section of the wire from the center to r=0.5R?
32. A cylindrical wire has a current density from the center of the wire’s cross section as J(r)=Cr2 where r is in meters, J is in amps per square meter, and C=103 A/m4. This current density continues to the end of the wire at a radius of 1.0 mm. Calculate the current just outside of this wire.
33. The current supplied to an air conditioner unit is 4.00 amps. The air conditioner is wired using a 10-gauge (diameter 2.588 mm) wire. The charge density is n=8.48×1028electronsm3. Find the magnitude of
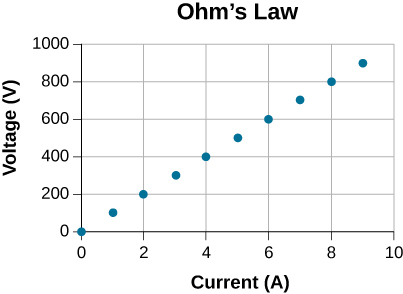
(a) current density and
(b) the drift velocity.
9.4 Resistivity and Resistance
34. What current flows through the bulb of a 3.00-V flashlight when its hot resistance is 3.60Ω?
35. Calculate the effective resistance of a pocket calculator that has a 1.35-V battery and through which 0.200 mA flows.
36. How many volts are supplied to operate an indicator light on a DVD player that has a resistance of 140Ω, given that 25.0 mA passes through it?
37. What is the resistance of a 20.0-m-long piece of 12-gauge copper wire having a 2.053-mm diameter?
38. The diameter of 0-gauge copper wire is 8.252 mm. Find the resistance of a 1.00-km length of such wire used for power transmission.
39. If the 0.100-mm-diameter tungsten filament in a light bulb is to have a resistance of 0.200Ω at 20.0°C, how long should it be?
40. A lead rod has a length of 30.00 cm and a resistance of 5.00μΩ. What is the radius of the rod?
41. Find the ratio of the diameter of aluminum to copper wire, if they have the same resistance per unit length (as they might in household wiring).
42. What current flows through a 2.54-cm-diameter rod of pure silicon that is 20.0 cm long, when 1.00×103 is applied to it? (Such a rod may be used to make nuclear-particle detectors, for example.)
43. (a) To what temperature must you raise a copper wire, originally at 20.0°C, to double its resistance, neglecting any changes in dimensions? (b) Does this happen in household wiring under ordinary circumstances?
44. A resistor made of nichrome wire is used in an application where its resistance cannot change more than 1.00% from its value at 20.0°C. Over what temperature range can it be used?
45. Of what material is a resistor made if its resistance is 40.0% greater at 100.0°C than at 20.0°C?
46. An electronic device designed to operate at any temperature in the range from −10.0°C to 55.0°C contains pure carbon resistors. By what factor does their resistance increase over this range?47.
(a) Of what material is a wire made, if it is 25.0 m long with a diameter of 0.100 mm and has a resistance of 77.7Ω at 20.0°C? (b) What is its resistance at 150.0°C?
48. Assuming a constant temperature coefficient of resistivity, what is the maximum percent decrease in the resistance of a constantan wire starting at 20.0°C?
49. A copper wire has a resistance of 0.500Ω at 20.0°C, and an iron wire has a resistance of 0.525Ω at the same temperature. At what temperature are their resistances equal?
9.5 Ohm's Law
50. A 2.2-kΩ resistor is connected across a D cell battery (1.5 V). What is the current through the resistor?
51. A resistor rated at 250kΩ is connected across two D cell batteries (each 1.50 V) in series, with a total voltage of 3.00 V. The manufacturer advertises that their resistors are within 5% of the rated value. What are the possible minimum current and maximum current through the resistor?
52. A resistor is connected in series with a power supply of 20.00 V. The current measure is 0.50 A. What is the resistance of the resistor?
53. A resistor is placed in a circuit with an adjustable voltage source. The voltage across and the current through the resistor and the measurements are shown below. Estimate the resistance of the resistor.
54. The following table show the measurements of a current through and the voltage across a sample of material. Plot the data, and assuming the object is an ohmic device, estimate the resistance.
| I(A) | V(V) |
|---|---|
| 0 | 3 |
| 2 | 23 |
| 4 | 39 |
| 6 | 58 |
| 8 | 77 |
| 10 | 100 |
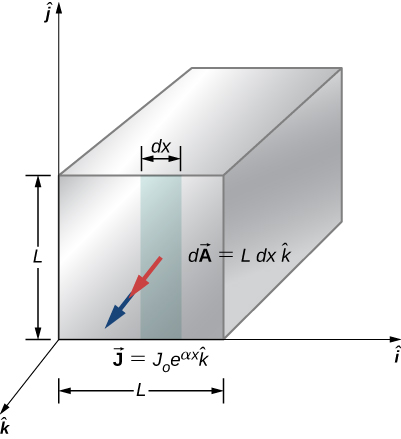
| 12 | 119 |
| 14 | 142 |
| 16 | 162 |
9.6 Electrical Energy and Power
55. A 20.00-V battery is used to supply current to a 10-kΩ resistor. Assume the voltage drop across any wires used for connections is negligible.
(a) What is the current through the resistor?
(b) What is the power dissipated by the resistor?
(c) What is the power input from the battery, assuming all the electrical power is dissipated by the resistor?
(d) What happens to the energy dissipated by the resistor?
56. What is the maximum voltage that can be applied to a 20-kΩ resistor rated at 14W?
57. A heater is being designed that uses a coil of 14-gauge nichrome wire to generate 300 W using a voltage of V=110V. How long should the engineer make the wire?
58. An alternative to CFL bulbs and incandescent bulbs are light-emitting diode (LED) bulbs. A 100-W incandescent bulb can be replaced by a 16-W LED bulb. Both produce 1600 lumens of light. Assuming the cost of electricity is $0.10 per kilowatt-hour, how much does it cost to run the bulb for one year if it runs for four hours a day?
59. The power dissipated by a resistor with a resistance of R=100Ω is P=2.0W. What are the current through and the voltage drop across the resistor?
60. Running late to catch a plane, a driver accidentally leaves the headlights on after parking the car in the airport parking lot. During takeoff, the driver realizes the mistake. Having just replaced the battery, the driver knows that the battery is a 12-V automobile battery, rated at 100 A⋅h. The driver, knowing there is nothing that can be done, estimates how long the lights will shine, assuming there are two 12-V headlights, each rated at 40 W. What did the driver conclude?
61. A physics student has a single-occupancy dorm room. The student has a small refrigerator that runs with a current of 3.00 A and a voltage of 110 V, a lamp that contains a 100-W bulb, an overhead light with a 60-W bulb, and various other small devices adding up to 3.00 W.
(a) Assuming the power plant that supplies 110 V electricity to the dorm is 10 km away and the two aluminum transmission cables use 0-gauge wire with a diameter of 8.252 mm, estimate the percentage of the total power supplied by the power company that is lost in the transmission.
(b) What would be the result is the power company delivered the electric power at 110 kV?
62. A 0.50-W, 220-Ω resistor carries the maximum current possible without damaging the resistor. If the current were reduced to half the value, what would be the power consumed?
9.7 Superconductors
63. Consider a power plant is located 60 km away from a residential area uses 0-gauge (A=42.40mm2) wire of copper to transmit power at a current of I=100.00A. How much more power is dissipated in the copper wires than it would be in superconducting wires?
64. A wire is drawn through a die, stretching it to four times its original length. By what factor does its resistance increase?
65. Digital medical thermometers determine temperature by measuring the resistance of a semiconductor device called a thermistor (which has α=−0.06/°C) when it is at the same temperature as the patient. What is a patient’s temperature if the thermistor’s resistance at that temperature is 82.0% of its value at 37°C (normal body temperature)?
66. Electrical power generators are sometimes “load tested” by passing current through a large vat of water. A similar method can be used to test the heat output of a resistor. A R=30Ω resistor is connected to a 9.0-V battery and the resistor leads are waterproofed and the resistor is placed in 1.0 kg of room temperature water (T=20°C). Current runs through the resistor for 20 minutes. Assuming all the electrical energy dissipated by the resistor is converted to heat, what is the final temperature of the water?
67. A 12-guage gold wire has a length of 1 meter.
(a) What would be the length of a silver 12-gauge wire with the same resistance?
(b) What are their respective resistances at the temperature of boiling water?
68. What is the change in temperature required to decrease the resistance for a carbon resistor by 10%?
Additional Problems
69. A coaxial cable consists of an inner conductor with radius ri=0.25cm and an outer radius of ro=0.5cm and has a length of 10 meters. Plastic, with a resistivity of ρ=2.00×1013Ω⋅m, separates the two conductors. What is the resistance of the cable?
70. A 10.00-meter long wire cable that is made of copper has a resistance of 0.051 ohms.
(a) What is the weight if the wire was made of copper?
(b) What is the weight of a 10.00-meter-long wire of the same gauge made of aluminum?
(c)What is the resistance of the aluminum wire? The density of copper is 8960kg/m3 and the density of aluminum is 2760kg/m3.
71. A nichrome rod that is 3.00 mm long with a cross-sectional area of 1.00mm2 is used for a digital thermometer.
(a) What is the resistance at room temperature?
(b) What is the resistance at body temperature?
72. The temperature in Philadelphia, PA can vary between 68.00°F and 100.00°F in one summer day. By what percentage will an aluminum wire’s resistance change during the day?
73. When 100.0 V is applied across a 5-gauge (diameter 4.621 mm) wire that is 10 m long, the magnitude of the current density is 2.0×108A/m2. What is the resistivity of the wire?
74. A wire with a resistance of 5.0Ω is drawn out through a die so that its new length is twice times its original length. Find the resistance of the longer wire. You may assume that the resistivity and density of the material are unchanged.
75. What is the resistivity of a wire of 5-gauge wire (A=16.8×10−6m2), 5.00 m length, and 5.10mΩ resistance?
76. Coils are often used in electrical and electronic circuits. Consider a coil which is formed by winding 1000 turns of insulated 20-gauge copper wire (area 0.52mm2) in a single layer on a cylindrical non-conducting core of radius 2.0 mm. What is the resistance of the coil? Neglect the thickness of the insulation.
77. Currents of approximately 0.06 A can be potentially fatal. Currents in that range can make the heart fibrillate (beat in an uncontrolled manner). The resistance of a dry human body can be approximately 100kΩ.
(a) What voltage can cause 0.2 A through a dry human body?
(b) When a human body is wet, the resistance can fall to 100Ω. What voltage can cause harm to a wet body?
78. A 20.00-ohm, 5.00-watt resistor is placed in series with a power supply.
(a) What is the maximum voltage that can be applied to the resistor without harming the resistor?
(b) What would be the current through the resistor?
79. A battery with an emf of 24.00 V delivers a constant current of 2.00 mA to an appliance. How much work does the battery do in three minutes?
80. A 12.00-V battery has an internal resistance of a tenth of an ohm.
(a) What is the current if the battery terminals are momentarily shorted together?
(b) What is the terminal voltage if the battery delivers 0.25 amps to a circuit?
Challenge Problems
81. A 10-gauge copper wire has a cross-sectional area A=5.26mm2 and carries a current of I=5.00A. The density of copper is ρ=89.50g/cm3. One mole of copper atoms (6.02×1023atoms) has a mass of approximately 63.50 g. What is the magnitude of the drift velocity of the electrons, assuming that each copper atom contributes one free electron to the current?
82. The current through a 12-gauge wire is given as I(t)=(5.00A)sin(2π60Hzt). What is the current density at time 15.00 ms?
83. A particle accelerator produces a beam with a radius of 1.25 mm with a current of 2.00 mA. Each proton has a kinetic energy of 10.00 MeV.
(a) What is the velocity of the protons?
(b) What is the number (n) of protons per unit volume?
(c) How many electrons pass a cross sectional area each second?
84. In this chapter, most examples and problems involved direct current (DC). DC circuits have the current flowing in one direction, from positive to negative. When the current was changing, it was changed linearly from I=−Imax to I=+Imax and the voltage changed linearly from V=−Vmax to V=+Vmax, where Vmax=ImaxR. Suppose a voltage source is placed in series with a resistor of R=10Ω that supplied a current that alternated as a sine wave, for example, I(t)=(3.00A)sin(2π4.00st). (a) What would a graph of the voltage drop across the resistor V(t) versus time look like? (b) What would a plot of V(t) versus I(t) for one period look like? (Hint: If you are not sure, try plotting V(t) versus I(t) using a spreadsheet.)
85. A current of I=25A is drawn from a 100-V battery for 30 seconds. By how much is the chemical energy reduced?
86. Consider a square rod of material with sides of length L=3.00cm with a current density of J=J0eαxk̂=(0.35Am2)e(2.1×10−3m−1)xk̂ as shown below. Find the current that passes through the face of
87. A resistor of an unknown resistance is placed in an insulated container filled with 0.75 kg of water. A voltage source is connected in series with the resistor and a current of 1.2 amps flows through the resistor for 10 minutes. During this time, the temperature of the water is measured and the temperature change during this time is ΔT=10.00°C.
(a) What is the resistance of the resistor?
(b) What is the voltage supplied by the power supply?
88. The charge that flows through a point in a wire as a function of time is modeled as q(t)=q0e−t/T=10.0Ce−t/5s.
(a) What is the initial current through the wire at time t=0.00s?
(b) Find the current at time t=12T.
(c) At what time t will the current be reduced by one-half I=12I0?
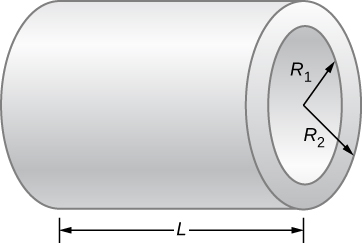
89. Consider a resistor made from a hollow cylinder of carbon as shown below. The inner radius of the cylinder is Ri=0.20mmRi=0.20mm and the outer radius is R0=0.30mm. The length of the resistor is L=0.90mm. The resistivity of the carbon is ρ=3.5×10−5Ω⋅m. (a) Prove that the resistance perpendicular from the axis is R=ρ2πLln(R0Ri). (b) What is the resistance?
90. What is the current through a cylindrical wire of radius R=0.1mm if the current density is J=J0Rr, where J0=32000Am2?
91. A student uses a 100.00-W, 115.00-V radiant heater to heat the student’s dorm room, during the hours between sunset and sunrise, 6:00 p.m. to 7:00 a.m.
(a) What current does the heater operate at?
(b) How many electrons move through the heater?
(c) What is the resistance of the heater?
(d) How much heat was added to the dorm room?
92. A 12-V car battery is used to power a 20.00-W, 12.00-V lamp during the physics club camping trip/star party. The cable to the lamp is 2.00 meters long, 14-gauge copper wire with a charge density of n=9.50×1028m−3.
(a) What is the current draw by the lamp?
(b) How long would it take an electron to get from the battery to the lamp?
93. A physics student uses a 115.00-V immersion heater to heat 400.00 grams (almost two cups) of water for herbal tea. During the two minutes it takes the water to heat, the physics student becomes bored and decides to figure out the resistance of the heater. The student starts with the assumption that the water is initially at the temperature of the room T_i=25.00°C and reaches T_f=100.00°C. The specific heat of the water is c=4180\frac{J}{kg}. What is the resistance of the heater?


