2.E: Geometric Optics and Image Formation (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
2.1 Images Formed by Plane Mirrors
1. What are the differences between real and virtual images? How can you tell (by looking) whether an image formed by a single lens or mirror is real or virtual?
2. Can you see a virtual image? Explain your response.
3. Can you photograph a virtual image?
4. Can you project a virtual image onto a screen?
5. Is it necessary to project a real image onto a screen to see it?
6. Devise an arrangement of mirrors allowing you to see the back of your head. What is the minimum number of mirrors needed for this task?
7. If you wish to see your entire body in a flat mirror (from head to toe), how tall should the mirror be? Does its size depend upon your distance away from the mirror? Provide a sketch.
2.2 Spherical Mirrors
8. At what distance is an image always located: at do,di, or f ?
9. Under what circumstances will an image be located at the focal point of a spherical lens or mirror?
10. What is meant by a negative magnification? What is meant by a magnification whose absolute value is less than one?
11. Can an image be larger than the object even though its magnification is negative? Explain.
2.3 Images Formed by Refraction
12. Derive the formula for the apparent depth of a fish in a fish tank using Snell’s law.
13. Use a ruler and a protractor to find the image by refraction in the following cases. Assume an air-glass interface. Use a refractive index of 1 for air and of 1.5 for glass. (Hint: Use Snell’s law at the interface.)
(a) A point object located on the axis of a concave interface located at a point within the focal length from the vertex.
(b) A point object located on the axis of a concave interface located at a point farther than the focal length from the vertex.
(c) A point object located on the axis of a convex interface located at a point within the focal length from the vertex.
(d) A point object located on the axis of a convex interface located at a point farther than the focal length from the vertex.
(e) Repeat (a)–(d) for a point object off the axis.
2.4 Thin Lenses
14. You can argue that a flat piece of glass, such as in a window, is like a lens with an infinite focal length. If so, where does it form an image? That is, how are di and do related?
15. When you focus a camera, you adjust the distance of the lens from the film. If the camera lens acts like a thin lens, why can it not be a fixed distance from the film for both near and distant objects?
16. A thin lens has two focal points, one on either side of the lens at equal distances from its center, and should behave the same for light entering from either side. Look backward and forward through a pair of eyeglasses and comment on whether they are thin lenses.
17. Will the focal length of a lens change when it is submerged in water? Explain.
2.5 The Eye
18. If the lens of a person’s eye is removed because of cataracts (as has been done since ancient times), why would you expect an eyeglass lens of about 16 D to be prescribed?
19. When laser light is shone into a relaxed normal-vision eye to repair a tear by spot-welding the retina to the back of the eye, the rays entering the eye must be parallel. Why?
20. Why is your vision so blurry when you open your eyes while swimming under water? How does a face mask enable clear vision?
21. It has become common to replace the cataract-clouded lens of the eye with an internal lens. This intraocular lens can be chosen so that the person has perfect distant vision. Will the person be able to read without glasses? If the person was nearsighted, is the power of the intraocular lens greater or less than the removed lens?
22. If the cornea is to be reshaped (this can be done surgically or with contact lenses) to correct myopia, should its curvature be made greater or smaller? Explain.
2.8 Microscopes and Telescopes
23. Geometric optics describes the interaction of light with macroscopic objects. Why, then, is it correct to use geometric optics to analyze a microscope’s image?
24. The image produced by the microscope in Figure 2.38 cannot be projected. Could extra lenses or mirrors project it? Explain.
25. If you want your microscope or telescope to project a real image onto a screen, how would you change the placement of the eyepiece relative to the objective?
Problems
2.1 Images Formed by Plane Mirrors
26. Consider a pair of flat mirrors that are positioned so that they form an angle of 120°. An object is placed on the bisector between the mirrors. Construct a ray diagram as in Figure 2.4 to show how many images are formed.
27. Consider a pair of flat mirrors that are positioned so that they form an angle of 60°. An object is placed on the bisector between the mirrors. Construct a ray diagram as in Figure 2.4 to show how many images are formed.
28. By using more than one flat mirror, construct a ray diagram showing how to create an inverted image.
2.2 Spherical Mirrors
29. The following figure shows a light bulb between two spherical mirrors. One mirror produces a beam of light with parallel rays; the other keeps light from escaping without being put into the beam. Where is the filament of the light in relation to the focal point or radius of curvature of each mirror?
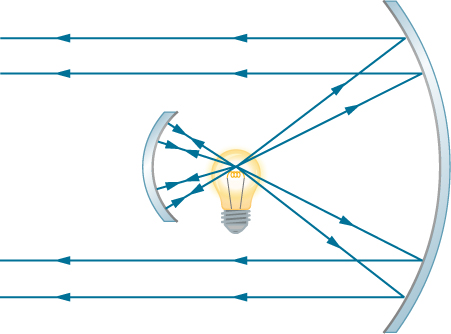
A light bulb is shown in the centre, with a small concave mirror to its left and a bigger one to its right. The light rays originating from the bulb that hit the smaller mirror are reflected back to the bulb. Light rays from the bulb that hit the bigger mirror are reflected. These reflected rays are parallel and travel towards the left.
30. Why are diverging mirrors often used for rearview mirrors in vehicles? What is the main disadvantage of using such a mirror compared with a flat one?
31. Some telephoto cameras use a mirror rather than a lens. What radius of curvature mirror is needed to replace a 800 mm-focal length telephoto lens?
32. Calculate the focal length of a mirror formed by the shiny back of a spoon that has a 3.00 cm radius of curvature.
33. Electric room heaters use a concave mirror to reflect infrared (IR) radiation from hot coils. Note that IR radiation follows the same law of reflection as visible light. Given that the mirror has a radius of curvature of 50.0 cm and produces an image of the coils 3.00 m away from the mirror, where are the coils?
34. Find the magnification of the heater element in the previous problem. Note that its large magnitude helps spread out the reflected energy.
35. What is the focal length of a makeup mirror that produces a magnification of 1.50 when a person’s face is 12.0 cm away? Explicitly show how you follow the steps in the Example 2.2.
36. A shopper standing 3.00 m from a convex security mirror sees his image with a magnification of 0.250.
(a) Where is his image?
(b) What is the focal length of the mirror?
(c) What is its radius of curvature?
37. An object 1.50 cm high is held 3.00 cm from a person’s cornea, and its reflected image is measured to be 0.167 cm high.
(a) What is the magnification?
(b) Where is the image?
(c) Find the radius of curvature of the convex mirror formed by the cornea. (Note that this technique is used by optometrists to measure the curvature of the cornea for contact lens fitting. The instrument used is called a keratometer, or curve measurer.)
38. Ray tracing for a flat mirror shows that the image is located a distance behind the mirror equal to the distance of the object from the mirror. This is stated as di=−do, since this is a negative image distance (it is a virtual image). What is the focal length of a flat mirror?
39. Show that, for a flat mirror, hi=ho, given that the image is the same distance behind the mirror as the distance of the object from the mirror.
40. Use the law of reflection to prove that the focal length of a mirror is half its radius of curvature. That is, prove that f=R/2. Note this is true for a spherical mirror only if its diameter is small compared with its radius of curvature.
41. Referring to the electric room heater considered in problem 5, calculate the intensity of IR radiation in W/m2 projected by the concave mirror on a person 3.00 m away. Assume that the heating element radiates 1500 W and has an area of 100cm2, and that half of the radiated power is reflected and focused by the mirror.
42. Two mirrors are inclined at an angle of 60° and an object is placed at a point that is equidistant from the two mirrors. Use a protractor to draw rays accurately and locate all images. You may have to draw several figures so that that rays for different images do not clutter your drawing.
43. Two parallel mirrors are facing each other and are separated by a distance of 3 cm. A point object is placed between the mirrors 1 cm from one of the mirrors. Find the coordinates of all the images.
2.3 Images Formed by Refraction
44. An object is located in air 30 cm from the vertex of a concave surface made of glass with a radius of curvature 10 cm. Where does the image by refraction form and what is its magnification? Use nair=1 and nglass=1.5.
45. An object is located in air 30 cm from the vertex of a convex surface made of glass with a radius of curvature 80 cm. Where does the image by refraction form and what is its magnification?
46. An object is located in water 15 cm from the vertex of a concave surface made of glass with a radius of curvature 10 cm. Where does the image by refraction form and what is its magnification? Use nwater=4/3 and nglass=1.5.
47. An object is located in water 30 cm from the vertex of a convex surface made of Plexiglas with a radius of curvature of 80 cm. Where does the image form by refraction and what is its magnification? nwater=4/3 and nPlexiglas=1.65.
48. An object is located in air 5 cm from the vertex of a concave surface made of glass with a radius of curvature 20 cm. Where does the image form by refraction and what is its magnification? Use nair=1 and nglass=1.5.
49. Derive the spherical interface equation for refraction at a concave surface. (Hint: Follow the derivation in the text for the convex surface.)
2.4 Thin Lenses
50. How far from the lens must the film in a camera be, if the lens has a 35.0-mm focal length and is being used to photograph a flower 75.0 cm away? Explicitly show how you follow the steps in the Figure 2.27.
51. A certain slide projector has a 100 mm-focal length lens.
(a) How far away is the screen if a slide is placed 103 mm from the lens and produces a sharp image?
(b) If the slide is 24.0 by 36.0 mm, what are the dimensions of the image? Explicitly show how you follow the steps in the Figure 2.27.
52. A doctor examines a mole with a 15.0-cm focal length magnifying glass held 13.5 cm from the mole.
(a) Where is the image?
(b) What is its magnification?
(c) How big is the image of a 5.00 mm diameter mole?
53. A camera with a 50.0-mm focal length lens is being used to photograph a person standing 3.00 m away.
(a) How far from the lens must the film be?
(b) If the film is 36.0 mm high, what fraction of a 1.75-m-tall person will fit on it?
(c) Discuss how reasonable this seems, based on your experience in taking or posing for photographs.
54. A camera lens used for taking close-up photographs has a focal length of 22.0 mm. The farthest it can be placed from the film is 33.0 mm.
(a) What is the closest object that can be photographed?
(b) What is the magnification of this closest object?
55. Suppose your 50.0 mm-focal length camera lens is 51.0 mm away from the film in the camera.
(a) How far away is an object that is in focus?
(b) What is the height of the object if its image is 2.00 cm high?
56. What is the focal length of a magnifying glass that produces a magnification of 3.00 when held 5.00 cm from an object, such as a rare coin?
57. The magnification of a book held 7.50 cm from a 10.0 cm-focal length lens is 4.00.
(a) Find the magnification for the book when it is held 8.50 cm from the magnifier.
(b) Repeat for the book held 9.50 cm from the magnifier.
(c) Comment on how magnification changes as the object distance increases as in these two calculations.
58. Suppose a 200 mm-focal length telephoto lens is being used to photograph mountains 10.0 km away.
(a) Where is the image?
(b) What is the height of the image of a 1000 m high cliff on one of the mountains?
59. A camera with a 100 mm-focal length lens is used to photograph the sun. What is the height of the image of the sun on the film, given the sun is 1.40×106km in diameter and is 1.50×108km away?
60. Use the thin-lens equation to show that the magnification for a thin lens is determined by its focal length and the object distance and is given by m=f/(f−do).
61. An object of height 3.0 cm is placed 5.0 cm in front of a converging lens of focal length 20 cm and observed from the other side. Where and how large is the image?
62. An object of height 3.0 cm is placed at 5.0 cm in front of a diverging lens of focal length 20 cm and observed from the other side. Where and how large is the image?
63. An object of height 3.0 cm is placed at 25 cm in front of a diverging lens of focal length 20 cm. Behind the diverging lens, there is a converging lens of focal length 20 cm. The distance between the lenses is 5.0 cm. Find the location and size of the final image.
64. Two convex lenses of focal lengths 20 cm and 10 cm are placed 30 cm apart, with the lens with the longer focal length on the right. An object of height 2.0 cm is placed midway between them and observed through each lens from the left and from the right. Describe what you will see, such as where the image(s) will appear, whether they will be upright or inverted and their magnifications.
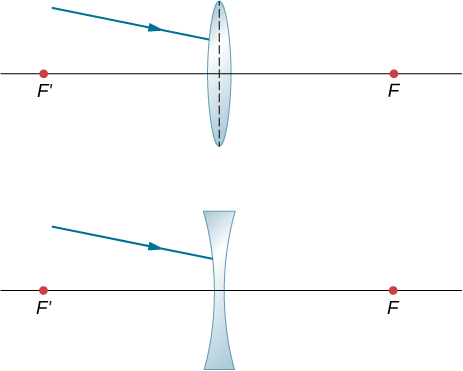
2.5 The Eye
Unless otherwise stated, the lens-to-retina distance is 2.00 cm.
65. What is the power of the eye when viewing an object 50.0 cm away?
66. Calculate the power of the eye when viewing an object 3.00 m away.
67. The print in many books averages 3.50 mm in height. How high is the image of the print on the retina when the book is held 30.0 cm from the eye?
68. Suppose a certain person’s visual acuity is such that he can see objects clearly that form an image 4.00μm high on his retina. What is the maximum distance at which he can read the 75.0-cm-high letters on the side of an airplane?
69. People who do very detailed work close up, such as jewelers, often can see objects clearly at much closer distance than the normal 25 cm.
(a) What is the power of the eyes of a woman who can see an object clearly at a distance of only 8.00 cm?
(b) What is the image size of a 1.00-mm object, such as lettering inside a ring, held at this distance?
(c) What would the size of the image be if the object were held at the normal 25.0 cm distance?
70. What is the far point of a person whose eyes have a relaxed power of 50.5 D?
71. What is the near point of a person whose eyes have an accommodated power of 53.5 D?
72. (a) A laser reshaping the cornea of a myopic patient reduces the power of his eye by 9.00 D, with a ±5.0 uncertainty in the final correction. What is the range of diopters for eyeglass lenses that this person might need after this procedure?
(b) Was the person nearsighted or farsighted before the procedure? How do you know?
73. The power for normal close vision is 54.0 D. In a vision-correction procedure, the power of a patient’s eye is increased by 3.00 D. Assuming that this produces normal close vision, what was the patient’s near point before the procedure?
74. For normal distant vision, the eye has a power of 50.0 D. What was the previous far point of a patient who had laser vision correction that reduced the power of her eye by 7.00 D, producing normal distant vision?
75. The power for normal distant vision is 50.0 D. A severely myopic patient has a far point of 5.00 cm. By how many diopters should the power of his eye be reduced in laser vision correction to obtain normal distant vision for him?
76. A student’s eyes, while reading the blackboard, have a power of 51.0 D. How far is the board from his eyes?
77. The power of a physician’s eyes is 53.0 D while examining a patient. How far from her eyes is the object that is being examined?
78. The normal power for distant vision is 50.0 D. A young woman with normal distant vision has a 10.0% ability to accommodate (that is, increase) the power of her eyes. What is the closest object she can see clearly?
79. The far point of a myopic administrator is 50.0 cm.
(a) What is the relaxed power of his eyes?
(b) If he has the normal 8.00% ability to accommodate, what is the closest object he can see clearly?
80. A very myopic man has a far point of 20.0 cm. What power contact lens (when on the eye) will correct his distant vision?
81. Repeat the previous problem for eyeglasses held 1.50 cm from the eyes.
82. A myopic person sees that her contact lens prescription is –4.00 D. What is her far point?
83. Repeat the previous problem for glasses that are 1.75 cm from the eyes.
84. The contact lens prescription for a mildly farsighted person is 0.750 D, and the person has a near point of 29.0 cm. What is the power of the tear layer between the cornea and the lens if the correction is ideal, taking the tear layer into account?
2.7 The Simple Magnifier
85. If the image formed on the retina subtends an angle of \displaystyle 30° and the object subtends an angle of \displaystyle 5°, what is the magnification of the image?
86. What is the magnification of a magnifying lens with a focal length of 10 cm if it is held 3.0 cm from the eye and the object is 12 cm from the eye?
87. How far should you hold a 2.1 cm-focal length magnifying glass from an object to obtain a magnification of \displaystyle 10×? Assume you place your eye 5.0 cm from the magnifying glass.
88. You hold a 5.0 cm-focal length magnifying glass as close as possible to your eye. If you have a normal near point, what is the magnification?
89. You view a mountain with a magnifying glass of focal length \displaystyle f=10cm. What is the magnification?
90. You view an object by holding a 2.5 cm-focal length magnifying glass 10 cm away from it. How far from your eye should you hold the magnifying glass to obtain a magnification of \displaystyle 10×?
91. A magnifying glass forms an image 10 cm on the opposite side of the lens from the object, which is 10 cm away. What is the magnification of this lens for a person with a normal near point if their eye 12 cm from the object?
92. An object viewed with the naked eye subtends a \displaystyle 2° angle. If you view the object through a \displaystyle 10× magnifying glass, what angle is subtended by the image formed on your retina?
93. For a normal, relaxed eye, a magnifying glass produces an angular magnification of 4.0. What is the largest magnification possible with this magnifying glass?
94. What range of magnification is possible with a 7.0 cm-focal length converging lens?
95. A magnifying glass produces an angular magnification of 4.5 when used by a young person with a near point of 18 cm. What is the maximum angular magnification obtained by an older person with a near point of 45 cm?
2.8 Microscopes and Telescopes
96. A microscope with an overall magnification of 800 has an objective that magnifies by 200.
(a) What is the angular magnification of the eyepiece?
(b) If there are two other objectives that can be used, having magnifications of 100 and 400, what other total magnifications are possible?
97. (a) What magnification is produced by a 0.150 cm-focal length microscope objective that is 0.155 cm from the object being viewed?
(b) What is the overall magnification if an \displaystyle 8× eyepiece (one that produces an angular magnification of 8.00) is used?
98. Where does an object need to be placed relative to a microscope for its 0.50 cm-focal length objective to produce a magnification of −400?
99. An amoeba is 0.305 cm away from the 0.300 cm-focal length objective lens of a microscope.
(a) Where is the image formed by the objective lens?
(b) What is this image’s magnification?
(c) An eyepiece with a 2.00-cm focal length is placed 20.0 cm from the objective. Where is the final image?
(d) What angular magnification is produced by the eyepiece?
(e) What is the overall magnification? (See Figure 2.39.)
100. Unreasonable Results Your friends show you an image through a microscope. They tell you that the microscope has an objective with a 0.500-cm focal length and an eyepiece with a 5.00-cm focal length. The resulting overall magnification is 250,000. Are these viable values for a microscope?
Unless otherwise stated, the lens-to-retina distance is 2.00 cm.
101. What is the angular magnification of a telescope that has a 100 cm-focal length objective and a 2.50 cm-focal length eyepiece?
102. Find the distance between the objective and eyepiece lenses in the telescope in the above problem needed to produce a final image very far from the observer, where vision is most relaxed. Note that a telescope is normally used to view very distant objects.
103. A large reflecting telescope has an objective mirror with a 10.0-m radius of curvature. What angular magnification does it produce when a 3.00 m-focal length eyepiece is used?
104. A small telescope has a concave mirror with a 2.00-m radius of curvature for its objective. Its eyepiece is a 4.00 cm-focal length lens.
(a) What is the telescope’s angular magnification?
(b) What angle is subtended by a 25,000 km-diameter sunspot?
(c) What is the angle of its telescopic image?
105. A 7.5×7.5× binocular produces an angular magnification of −7.50, acting like a telescope. (Mirrors are used to make the image upright.) If the binoculars have objective lenses with a 75.0-cm focal length, what is the focal length of the eyepiece lenses?
106. Construct Your Own Problem Consider a telescope of the type used by Galileo, having a convex objective and a concave eyepiece as illustrated in part (a) of Figure 2.40. Construct a problem in which you calculate the location and size of the image produced. Among the things to be considered are the focal lengths of the lenses and their relative placements as well as the size and location of the object. Verify that the angular magnification is greater than one. That is, the angle subtended at the eye by the image is greater than the angle subtended by the object.
107. Trace rays to find which way the given ray will emerge after refraction through the thin lens in the following figure. Assume thin-lens approximation. (Hint: Pick a point P on the given ray in each case. Treat that point as an object. Now, find its image Q. Use the rule: All rays on the other side of the lens will either go through Q or appear to be coming from Q.)
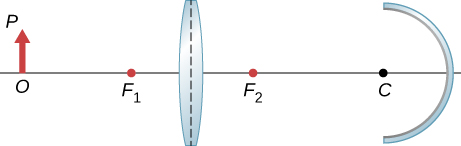
108. Copy and draw rays to find the final image in the following diagram. (Hint: Find the intermediate image through lens alone. Use the intermediate image as the object for the mirror and work with the mirror alone to find the final image.)
109. A concave mirror of radius of curvature 10 cm is placed 30 cm from a thin convex lens of focal length 15 cm. Find the location and magnification of a small bulb sitting 50 cm from the lens by using the algebraic method.
110. An object of height 3 cm is placed at 25 cm in front of a converging lens of focal length 20 cm. Behind the lens there is a concave mirror of focal length 20 cm. The distance between the lens and the mirror is 5 cm. Find the location, orientation and size of the final image.
111. An object of height 3 cm is placed at a distance of 25 cm in front of a converging lens of focal length 20 cm, to be referred to as the first lens. Behind the lens there is another converging lens of focal length 20 cm placed 10 cm from the first lens. There is a concave mirror of focal length 15 cm placed 50 cm from the second lens. Find the location, orientation, and size of the final image.
112. An object of height 2 cm is placed at 50 cm in front of a diverging lens of focal length 40 cm. Behind the lens, there is a convex mirror of focal length 15 cm placed 30 cm from the converging lens. Find the location, orientation, and size of the final image.
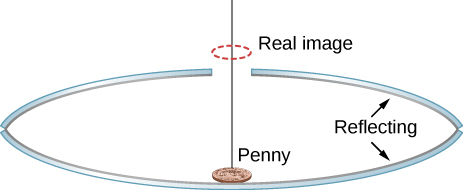
113. Two concave mirrors are placed facing each other. One of them has a small hole in the middle. A penny is placed on the bottom mirror (see the following figure). When you look from the side, a real image of the penny is observed above the hole. Explain how that could happen.
114. A lamp of height 5 cm is placed 40 cm in front of a converging lens of focal length 20 cm. There is a plane mirror 15 cm behind the lens. Where would you find the image when you look in the mirror?
115. Parallel rays from a faraway source strike a converging lens of focal length 20 cm at an angle of 15 degrees with the horizontal direction. Find the vertical position of the real image observed on a screen in the focal plane.
116. Parallel rays from a faraway source strike a diverging lens of focal length 20 cm at an angle of 10 degrees with the horizontal direction. As you look through the lens, where in the vertical plane the image would appear?
117. A light bulb is placed 10 cm from a plane mirror, which faces a convex mirror of radius of curvature 8 cm. The plane mirror is located at a distance of 30 cm from the vertex of the convex mirror. Find the location of two images in the convex mirror. Are there other images? If so, where are they located?
118. A point source of light is 50 cm in front of a converging lens of focal length 30 cm. A concave mirror with a focal length of 20 cm is placed 25 cm behind the lens. Where does the final image form, and what are its orientation and magnification?
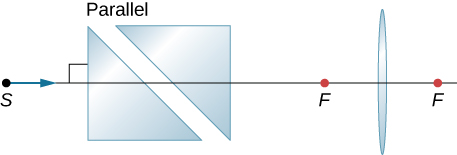
119. Copy and trace to find how a horizontal ray from S comes out after the lens. Use \displaystyle n_{glass}=1.5 for the prism material.
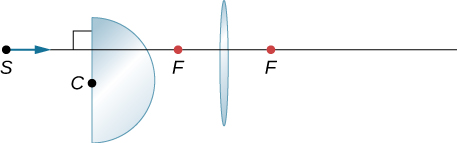
120. Copy and trace how a horizontal ray from S comes out after the lens. Use \displaystyle n=1.55 for the glass.
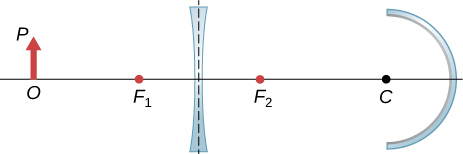
121. Copy and draw rays to figure out the final image.
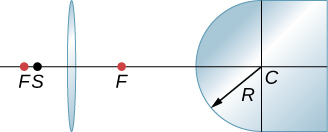
122. By ray tracing or by calculation, find the place inside the glass where rays from S converge as a result of refraction through the lens and the convex air-glass interface. Use a ruler to estimate the radius of curvature.
123. A diverging lens has a focal length of 20 cm. What is the power of the lens in diopters?
124. Two lenses of focal lengths of \displaystyle f_1 and \displaystyle f_2 are glued together with transparent material of negligible thickness. Show that the total power of the two lenses simply add.
125. What will be the angular magnification of a convex lens with the focal length 2.5 cm?
126. What will be the formula for the angular magnification of a convex lens of focal length f if the eye is very close to the lens and the near point is located a distance D from the eye?
Additional Problems
127. Use a ruler and a protractor to draw rays to find images in the following cases.
(a) A point object located on the axis of a concave mirror located at a point within the focal length from the vertex.
(b) A point object located on the axis of a concave mirror located at a point farther than the focal length from the vertex.
(c) A point object located on the axis of a convex mirror located at a point within the focal length from the vertex.
(d) A point object located on the axis of a convex mirror located at a point farther than the focal length from the vertex.
(e) Repeat (a)–(d) for a point object off the axis.
128. Where should a 3 cm tall object be placed in front of a concave mirror of radius 20 cm so that its image is real and 2 cm tall?
129. A 3 cm tall object is placed 5 cm in front of a convex mirror of radius of curvature 20 cm. Where is the image formed? How tall is the image? What is the orientation of the image?
130. You are looking for a mirror so that you can see a four-fold magnified virtual image of an object when the object is placed 5 cm from the vertex of the mirror. What kind of mirror you will need? What should be the radius of curvature of the mirror?
131. Derive the following equation for a convex mirror: \displaystyle \frac{1}{VO}−\frac{1}{VI}=−\frac{1}{VF}, where VO is the distance to the object O from vertex V, VI the distance to the image I from V, and VF is the distance to the focal point F from V. (Hint: use two sets of similar triangles.)
132. (a) Draw rays to form the image of a vertical object on the optical axis and farther than the focal point from a converging lens.
(b) Use plane geometry in your figure and prove that the magnification m is given by \displaystyle m=\frac{h_i}{h_o}=−\frac{d_i}{d_o}.
133. Use another ray-tracing diagram for the same situation as given in the previous problem to derive the thin-lens equation, \displaystyle \frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}.
134. You photograph a 2.0-m-tall person with a camera that has a 5.0 cm-focal length lens. The image on the film must be no more than 2.0 cm high.
(a) What is the closest distance the person can stand to the lens?
(b) For this distance, what should be the distance from the lens to the film?
135. Find the focal length of a thin plano-convex lens. The front surface of this lens is flat, and the rear surface has a radius of curvature of \displaystyle R_2=−35cm. Assume that the index of refraction of the lens is 1.5.
136. Find the focal length of a meniscus lens with \displaystyle R_1=20cm and \displaystyle R_2=15cm. Assume that the index of refraction of the lens is 1.5.
137. A nearsighted man cannot see objects clearly beyond 20 cm from his eyes. How close must he stand to a mirror in order to see what he is doing when he shaves?
138. A mother sees that her child’s contact lens prescription is 0.750 D. What is the child’s near point?
139. Repeat the previous problem for glasses that are 2.20 cm from the eyes.
140. The contact-lens prescription for a nearsighted person is −4.00 D and the person has a far point of 22.5 cm. What is the power of the tear layer between the cornea and the lens if the correction is ideal, taking the tear layer into account?
141. Unreasonable Results A boy has a near point of 50 cm and a far point of 500 cm. Will a −4.00 D lens correct his far point to infinity?
142. Find the angular magnification of an image by a magnifying glass of \displaystyle f=5.0cm if the object is placed \displaystyle d_o=4.0cm from the lens and the lens is close to the eye.
143. Let objective and eyepiece of a compound microscope have focal lengths of 2.5 cm and 10 cm, respectively and be separated by 12 cm. A \displaystyle 70-μm object is placed 6.0 cm from the objective. How large is the virtual image formed by the objective-eyepiece system?
144. Draw rays to scale to locate the image at the retina if the eye lens has a focal length 2.5 cm and the near point is 24 cm. (Hint: Place an object at the near point.)
145. The objective and the eyepiece of a microscope have the focal lengths 3 cm and 10 cm respectively. Decide about the distance between the objective and the eyepiece if we need a \displaystyle 10× magnification from the objective/eyepiece compound system.
146. A far-sighted person has a near point of 100 cm. How far in front or behind the retina does the image of an object placed 25 cm from the eye form? Use the cornea to retina distance of 2.5 cm.
147. A near-sighted person has afar point of 80 cm.
(a) What kind of corrective lens the person will need if the lens is to be placed 1.5 cm from the eye?
(b) What would be the power of the contact lens needed? Assume distance to contact lens from the eye to be zero.
148. In a reflecting telescope the objective is a concave mirror of radius of curvature 2 m and an eyepiece is a convex lens of focal length 5 cm. Find the apparent size of a 25-m tree at a distance of 10 km that you would perceive when looking through the telescope.
149. Two stars that are \displaystyle 10^9km apart are viewed by a telescope and found to be separated by an angle of \displaystyle 10^{−5}radians. If the eyepiece of the telescope has a focal length of 1.5 cm and the objective has a focal length of 3 meters, how far away are the stars from the observer?
150. What is the angular size of the Moon if viewed from a binocular that has a focal length of 1.2 cm for the eyepiece and a focal length of 8 cm for the objective? Use the radius of the moon \displaystyle 1.74×10^6m and the distance of the moon from the observer to be \displaystyle 3.8×10^8m.
151. An unknown planet at a distance of \displaystyle 10^{12}m from Earth is observed by a telescope that has a focal length of the eyepiece of 1 cm and a focal length of the objective of 1 m. If the far away planet is seen to subtend an angle of \displaystyle 10^{−5}radian at the eyepiece, what is the size of the planet?


