7.2: Wave functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the statistical interpretation of the wavefunction
- Use the wavefunction to determine probabilities
- Calculate expectation values of position, momentum, and kinetic energy
In the preceding chapter, we saw that particles act in some cases like particles and in other cases like waves. But what does it mean for a particle to “act like a wave”? What precisely is “waving”? What rules govern how this wave changes and propagates? How is the wavefunction used to make predictions? For example, if the amplitude of an electron wave is given by a function of position and time, Ψ(x,t), defined for all x, where exactly is the electron? The purpose of this chapter is to answer these questions.
Using the Wavefunction
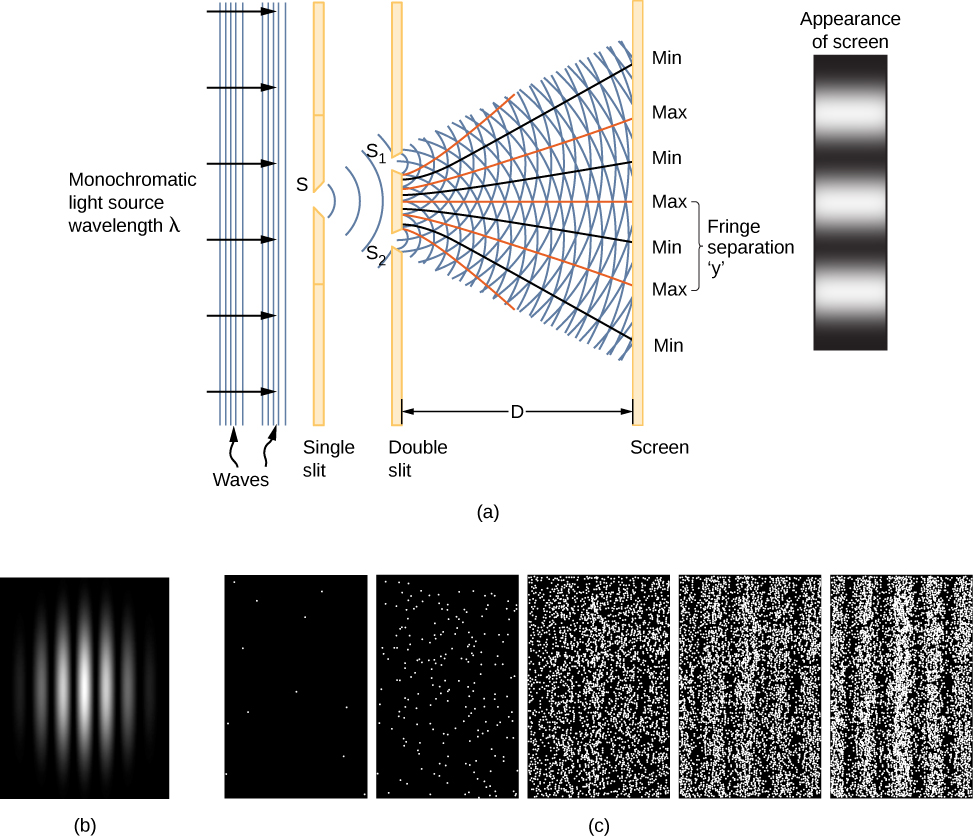
A clue to the physical meaning of the wavefunction Ψ(x,t) is provided by the two-slit interference of monochromatic light (Figure 7.2.1) that behave as electromagnetic waves. The wavefunction of a light wave is given by E(x,t), and its energy density is given by |E|2, where E is the electric field strength. The energy of an individual photon depends only on the frequency of light, ϵphoton=hf, so |E|2 is proportional to the number of photons. When light waves from S1 interfere with light waves from S2 at the viewing screen (a distance D away), an interference pattern is produced (7.2.1a). Bright fringes correspond to points of constructive interference of the light waves, and dark fringes correspond to points of destructive interference of the light waves (7.2.1b).
Suppose the screen is initially unexposed to light. If the screen is exposed to very weak light, the interference pattern appears gradually (Figure 7.2.1c, left to right). Individual photon hits on the screen appear as dots. The dot density is expected to be large at locations where the interference pattern will be, ultimately, the most intense. In other words, the probability (per unit area) that a single photon will strike a particular spot on the screen is proportional to the square of the total electric field, |E|2 at that point. Under the right conditions, the same interference pattern develops for matter particles, such as electrons.
Visit this interactive simulation to learn more about quantum wave interference.
The square of the matter wave |Ψ|2 in one dimension has a similar interpretation as the square of the electric field |E|2. It gives the probability that a particle will be found at a particular position and time per unit length, also called the probability density. The probability (P) a particle is found in a narrow interval (x, x + dx) at time t is therefore
P(x,x+dx)=|Ψ(x,t)|2dx.
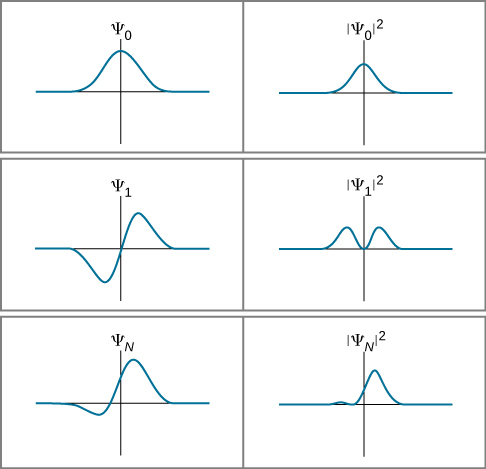
(Later, we define the magnitude squared for the general case of a function with “imaginary parts.”) This probabilistic interpretation of the wavefunction is called the Born interpretation. Examples of wavefunctions and their squares for a particular time t are given in Figure 7.2.2.
If the wavefunction varies slowly over the interval Δx, the probability a particle is found in the interval is approximately
P(x,x+Δx)≈|Ψ(x,t)|2δx.
Notice that squaring the wavefunction ensures that the probability is positive. (This is analogous to squaring the electric field strength—which may be positive or negative—to obtain a positive value of intensity.) However, if the wavefunction does not vary slowly, we must integrate:
P(x,x+Δx)=∫x+Δxx|Ψ(x,t)|2dx.
This probability is just the area under the function |Ψ(x,t)|2 between x and x+Δx. The probability of finding the particle “somewhere” (the normalization condition) is
P(−∞,+∞)=∫∞−∞|Ψ(x,t)|2dx=1.
For a particle in two dimensions, the integration is over an area and requires a double integral; for a particle in three dimensions, the integration is over a volume and requires a triple integral. For now, we stick to the simple one-dimensional case.
A ball is constrained to move along a line inside a tube of length L. The ball is equally likely to be found anywhere in the tube at some time t. What is the probability of finding the ball in the left half of the tube at that time? (The answer is 50%, of course, but how do we get this answer by using the probabilistic interpretation of the quantum mechanical wavefunction?)
Strategy
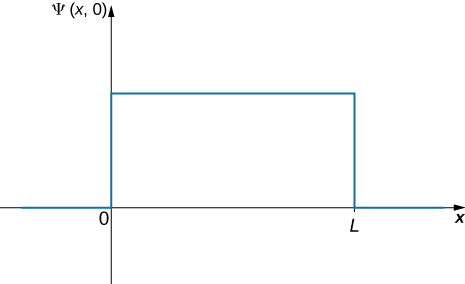
The first step is to write down the wavefunction. The ball is equally like to be found anywhere in the box, so one way to describe the ball with a constant wavefunction (Figure 7.2.3). The normalization condition can be used to find the value of the function and a simple integration over half of the box yields the final answer.
Solution
The wavefunction of the ball can be written as Ψ(x,t)=C(0<x<L), where C is a constant, and Ψ(x,t)=0 otherwise. We can determine the constant C by applying the normalization condition (we set t=0 to simplify the notation):
P(∞,+∞)=∫∞−∞|C|2dx=1.
This integral can be broken into three parts: (1) negative infinity to zero, (2) zero to L, and (3) L to infinity. The particle is constrained to be in the tube, so C=0 outside the tube and the first and last integrations are zero. The above equation can therefore be written
P(x=0,L)=∫L0|C|2dx=1.
The value C does not depend on x and can be taken out of the integral, so we obtain
|C|2∫L0dx=1.
Integration gives
C=√1L.
To determine the probability of finding the ball in the first half of the box (0<x<L), we have
P(x=0,L/2)=∫L/20|√1L|2dx=(1L)L2=0.50.
Significance
The probability of finding the ball in the first half of the tube is 50%, as expected. Two observations are noteworthy. First, this result corresponds to the area under the constant function from x=0 to L/2 (the area of a square left of L/2). Second, this calculation requires an integration of the square of the wavefunction. A common mistake in performing such calculations is to forget to square the wavefunction before integration.
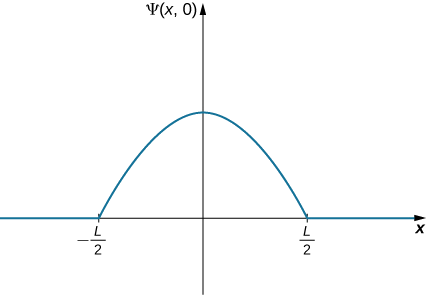
A ball is again constrained to move along a line inside a tube of length L. This time, the ball is found preferentially in the middle of the tube. One way to represent its wavefunction is with a simple cosine function (Figure 7.2.4). What is the probability of finding the ball in the last one-quarter of the tube?
Strategy
We use the same strategy as before. In this case, the wavefunction has two unknown constants: One is associated with the wavelength of the wave and the other is the amplitude of the wave. We determine the amplitude by using the boundary conditions of the problem, and we evaluate the wavelength by using the normalization condition. Integration of the square of the wavefunction over the last quarter of the tube yields the final answer. The calculation is simplified by centering our coordinate system on the peak of the wavefunction.
Solution
The wavefunction of the ball can be written
Ψ(x,t)=Acos(kx)(−L/2<x<L/2),
where A is the amplitude of the wavefunction and k=2π/λ is its wavenumber. Beyond this interval, the amplitude of the wavefunction is zero because the ball is confined to the tube. Requiring the wavefunction to terminate at the right end of the tube gives
Ψ(x=L2,0)=0.
Evaluating the wavefunction at x=L/2 gives
Acos(kL/2)=0.
This equation is satisfied if the argument of the cosine is an integral multiple of π/2, 3π/2, 5π/2, and so on. In this case, we have
kL2=π2, or k=πL.
Applying the normalization condition gives A=√2/L, so the wavefunction of the ball is
Ψ(x,0)=√2Lcos(πx/L),−L/2<x<L/2.
To determine the probability of finding the ball in the last quarter of the tube, we square the function and integrate:
P(x=L/4,L/2)=∫L/2L/4|√2Lcos(πxL)|2dx=0.091.
Significance
The probability of finding the ball in the last quarter of the tube is 9.1%. The ball has a definite wavelength (λ=2L). If the tube is of macroscopic length (L=1m), the momentum of the ball is
p=hλ=h2L≈10−36m/s.
This momentum is much too small to be measured by any human instrument.
An Interpretation of the Wavefunction
We are now in position to begin to answer the questions posed at the beginning of this section. First, for a traveling particle described by Ψ(x,t)=Asin(kx−ωt), what is “waving?” Based on the above discussion, the answer is a mathematical function that can, among other things, be used to determine where the particle is likely to be when a position measurement is performed. Second, how is the wavefunction used to make predictions? If it is necessary to find the probability that a particle will be found in a certain interval, square the wavefunction and integrate over the interval of interest. Soon, you will learn soon that the wavefunction can be used to make many other kinds of predictions, as well.
Third, if a matter wave is given by the wavefunction Ψ(x,t), where exactly is the particle? Two answers exist: (1) when the observer is not looking (or the particle is not being otherwise detected), the particle is everywhere (x=−∞,+∞); and (2) when the observer is looking (the particle is being detected), the particle “jumps into” a particular position state (x,x+dx) with a probability given by
P(x,x+dx)=|Ψ(x,t)|2dx
via a process called state reduction or wavefunction collapse. This answer is called the Copenhagen interpretation of the wavefunction, or of quantum mechanics.
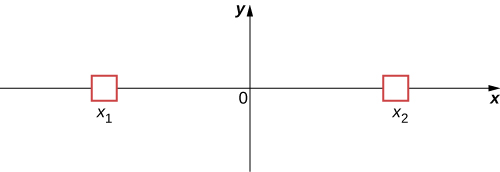
To illustrate this interpretation, consider the simple case of a particle that can occupy a small container either at x1 or x2 (Figure 7.2.5). In classical physics, we assume the particle is located either at x1 or x2 when the observer is not looking. However, in quantum mechanics, the particle may exist in a state of indefinite position—that is, it may be located at x1 and x2 when the observer is not looking. The assumption that a particle can only have one value of position (when the observer is not looking) is abandoned. Similar comments can be made of other measurable quantities, such as momentum and energy.
The bizarre consequences of the Copenhagen interpretation of quantum mechanics are illustrated by a creative thought experiment first articulated by Erwin Schrödinger (National Geographic, 2013) (7.2.6):
“A cat is placed in a steel box along with a Geiger counter, a vial of poison, a hammer, and a radioactive substance. When the radioactive substance decays, the Geiger detects it and triggers the hammer to release the poison, which subsequently kills the cat. The radioactive decay is a random [probabilistic] process, and there is no way to predict when it will happen. Physicists say the atom exists in a state known as a superposition—both decayed and not decayed at the same time. Until the box is opened, an observer doesn’t know whether the cat is alive or dead—because the cat’s fate is intrinsically tied to whether or not the atom has decayed and the cat would [according to the Copenhagen interpretation] be “living and dead ... in equal parts” until it is observed.”
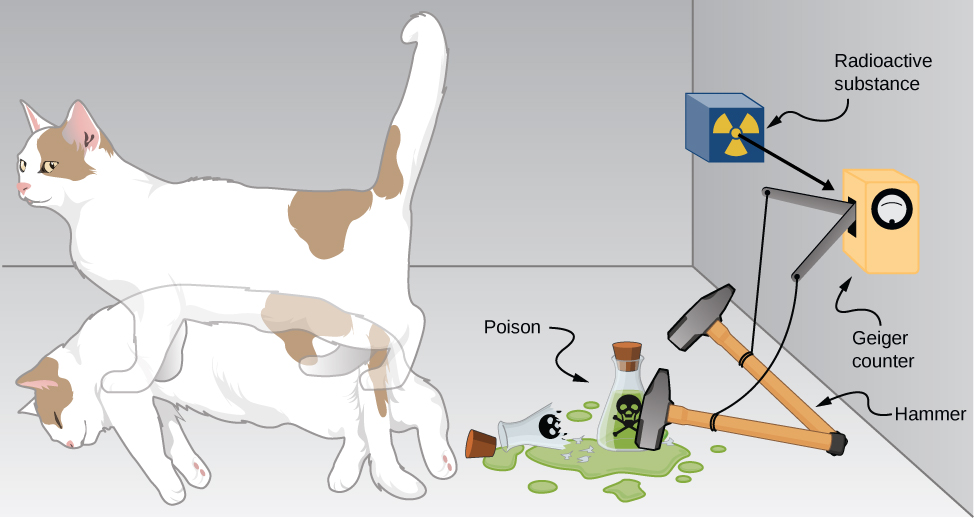
Schrödinger took the absurd implications of this thought experiment (a cat simultaneously dead and alive) as an argument against the Copenhagen interpretation. However, this interpretation remains the most commonly taught view of quantum mechanics.
Two-state systems (left and right, atom decays and does not decay, and so on) are often used to illustrate the principles of quantum mechanics. These systems find many applications in nature, including electron spin and mixed states of particles, atoms, and even molecules. Two-state systems are also finding application in the quantum computer, as mentioned in the introduction of this chapter. Unlike a digital computer, which encodes information in binary digits (zeroes and ones), a quantum computer stores and manipulates data in the form of quantum bits, or qubits. In general, a qubit is not in a state of zero or one, but rather in a mixed state of zero and one. If a large number of qubits are placed in the same quantum state, the measurement of an individual qubit would produce a zero with a probability p, and a one with a probability q=1−p. Some scientists believe that quantum computers are the future of the computer industry.
Complex Conjugates
Later in this section, you will see how to use the wavefunction to describe particles that are “free” or bound by forces to other particles. The specific form of the wavefunction depends on the details of the physical system. A peculiarity of quantum theory is that these functions are usually complex functions. A complex function is one that contains one or more imaginary numbers (i=√−1). Experimental measurements produce real (nonimaginary) numbers only, so the above procedure to use the wavefunction must be slightly modified. In general, the probability that a particle is found in the narrow interval (x,x+dx) at time t is given by
P(x,x+dx)=|Ψ(x,t)|2dx=Ψ∗(x,t)Ψ(x,t)dx,
where Ψ∗(x,t) is the complex conjugate of the wavefunction. The complex conjugate of a function is obtaining by replacing every occurrence of i=√−1 in that function with −i. This procedure eliminates complex numbers in all predictions because the product Ψ∗(x,t)Ψ(x,t) is always a real number.
If a=3+4i, what is the product a∗a?
- Answer
-
(3+4i)(3−4i)=9−16i2=25
Consider the motion of a free particle that moves along the x-direction. As the name suggests, a free particle experiences no forces and so moves with a constant velocity. As we will see in a later section of this chapter, a formal quantum mechanical treatment of a free particle indicates that its wavefunction has real and complex parts. In particular, the wavefunction is given by
Ψ(x,t)=Acos(kx−ωt)+iAsin(kx−ωt),
where A is the amplitude, k is the wave number, and ω is the angular frequency. Euler’s formula
eiϕ=cos(ϕ)+isin(ϕ)⏟Euler’s formula
can be used to rewrite Equation ??? in the form
Ψ(x,t)=Aei(kx−ωt)=Aeiϕ,
where ϕ is the phase angle. If the wavefunction varies slowly over the interval Δx, the probability of finding the particle in that interval is
P(x,x+Δx)≈Ψ∗(x,t)Ψ(x,t)Δx=(A∗e−iϕ)(Aeiϕ)Δx=(A∗A)Δx.
If A has real and complex parts (a+ib, where a and b are real constants), then
A∗A=(a−ib)(a+ib)=a2+b2.
Notice that the complex numbers have vanished. Thus,
P(x,x+Δx)≈|A|2δx
is a real quantity. The interpretation of Ψ∗(x,t)Ψ(x,t) as a probability density ensures that the predictions of quantum mechanics can be checked in the “real world.”
Suppose that a particle with energy E is moving along the x-axis and is confined in the region between 0 and L. One possible wavefunction is
ψ(x,t)={Ae−iEt/ℏsinπxL0≤x≤L0x<0 and x>L
Determine the normalization constant.
- Answer
-
A=√2/L
Expectation Values
In classical mechanics, the solution to an equation of motion is a function of a measurable quantity, such as x(t), where x is the position and t is the time. Note that the particle has one value of position for any time t. In quantum mechanics, however, the solution to an equation of motion is a wavefunction, Ψ(x,t). The particle has many values of position for any time t, and only the probability density of finding the particle, |Ψ(x,t)|2, can be known. The average value of position for a large number of particles with the same wavefunction is expected to be
⟨x⟩=∫∞−∞xP(x,t)dx=∫∞−∞xΨ∗(x,t)Ψ(x,t)dx.
This is called the expectation value of the position. It is usually written
⟨x⟩=∫∞−∞Ψ∗(x,t)xΨ(x,t)dx.
where the x is sandwiched between the wavefunctions. The reason for this will become apparent soon. Formally, x is called the position operator.
At this point, it is important to stress that a wavefunction can be written in terms of other quantities as well, such as velocity (v), momentum (p), and kinetic energy (K). The expectation value of momentum, for example, can be written
⟨p⟩=∫∞−∞Ψ∗(p,t)pΨ(p,t)dp,
where dp is used instead of dx to indicate an infinitesimal interval in momentum. In some cases, we know the wavefunction in position, Ψ(x,t), but seek the expectation of momentum. The procedure for doing this is
⟨p⟩=∫∞−∞Ψ∗(x,t)(−iℏddx)Ψ(x,t)dx,
where the quantity in parentheses, sandwiched between the wavefunctions, is called the momentum operator in the x-direction. [The momentum operator in Equation ??? is said to be the position-space representation of the momentum operator.] The momentum operator must act (operate) on the wavefunction to the right, and then the result must be multiplied by the complex conjugate of the wavefunction on the left, before integration. The momentum operator in the x-direction is sometimes denoted
⟨p⟩=−iℏddx,
Momentum operators for the y- and z-directions are defined similarly. This operator and many others are derived in a more advanced course in modern physics. In some cases, this derivation is relatively simple. For example, the kinetic energy operator is just
(K)op=12m(vx)2op=(px)2op2m=(−iℏddx)22m=−ℏ22m(ddx)(ddx).
Thus, if we seek an expectation value of kinetic energy of a particle in one dimension, two successive ordinary derivatives of the wavefunction are required before integration.
Expectation-value calculations are often simplified by exploiting the symmetry of wavefunctions. Symmetric wavefunctions can be even or odd. An even function is a function that satisfies
ψ(x)=ψ(−x).
In contrast, an odd function is a function that satisfies
ψ(x)=−ψ(−x).
An example of even and odd functions is shown in Figure 7.2.7. An even function is symmetric about the y-axis. This function is produced by reflecting ψ(x) for x>0 about the vertical y-axis. By comparison, an odd function is generated by reflecting the function about the y-axis and then about the x-axis. (An odd function is also referred to as an anti-symmetric function.)
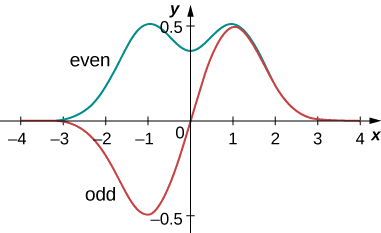
In general, an even function times an even function produces an even function. A simple example of an even function is the product x2e−x2 (even times even is even). Similarly, an odd function times an odd function produces an even function, such as x sin x (odd times odd is even). However, an odd function times an even function produces an odd function, such as x2e−x2 (odd times even is odd). The integral over all space of an odd function is zero, because the total area of the function above the x-axis cancels the (negative) area below it. As the next example shows, this property of odd functions is very useful.
The normalized wavefunction of a particle is
ψ(x)=e−|x|/x0/√x0.
Find the expectation value of position.
Strategy
Substitute the wavefunction into Equation ??? and evaluate. The position operator introduces a multiplicative factor only, so the position operator need not be “sandwiched.”
Solution
First multiply, then integrate:
⟨x⟩=∫∞−∞dxx|ψ(x)|2=∫∞−∞dxx|e−|x|/x0√x0|2=1x0∫∞−∞dxxe−2|x|/x0=0.
Significance
The function in the integrand (xe−2|x|/x0) is odd since it is the product of an odd function (x) and an even function (e−2|x|/x0). The integral vanishes because the total area of the function about the x-axis cancels the (negative) area below it. The result (⟨x⟩=0) is not surprising since the probability density function is symmetric about x=0.
The time-dependent wavefunction of a particle confined to a region between 0 and L is
ψ(x,t)=Ae−iωtsin(πx/L)
where ω is angular frequency and E is the energy of the particle. (Note: The function varies as a sine because of the limits (0 to L). When x=0, the sine factor is zero and the wavefunction is zero, consistent with the boundary conditions.) Calculate the expectation values of position, momentum, and kinetic energy.
Strategy
We must first normalize the wavefunction to find A. Then we use the operators to calculate the expectation values.
Solution
Computation of the normalization constant:
1=∫L0dxψ∗(x)ψ(x)=∫L0dx(Ae+iωtsinπxL)(Ae−iωtsinπxL)=A2∫L0dxsin2πxL=A2L2⇒A=√2L.
The expectation value of position is
⟨x⟩=∫L0dxψ∗(x)xψ(x)=∫L0dx(Ae+iωtsinπxL)x(Ae−iωtsinπxL)=A2∫L0dxxsin2πxL=A2L24⇒A=L2.
The expectation value of momentum in the x-direction also requires an integral. To set this integral up, the associated operator must— by rule—act to the right on the wavefunction ψ(x):
−iℏddxψ(x)=−iℏddxAe−iωtsinπxL=−iAh2Le−iωtcosπxL.
Therefore, the expectation value of momentum is
⟨p⟩=∫L0dx(Ae+iωtsinπxL)(−iAh2Le−iωtcosπxL)=−iA2h4L∫L0dxsin2πxL=0.
The function in the integral is a sine function with a wavelength equal to the width of the well, L—an odd function about x=L/2. As a result, the integral vanishes.
The expectation value of kinetic energy in the x-direction requires the associated operator to act on the wavefunction:
−ℏ22md2dx2ψ(x)=−ℏ22md2dx2Ae−iωtsinπxL=−ℏ22mAe−iωtd2dx2sinπxL=Ah28mL2e−iωtsinπxL.
Thus, the expectation value of the kinetic energy is
⟨K⟩=∫L0dx(Ae+iωtsinπxL)(Ah28mL2e−iωtsinπxL)=A2h28mL2∫L0dxsin2πxL=A2h28mL2L2=h28mL2.
Significance
The average position of a large number of particles in this state is L/2. The average momentum of these particles is zero because a given particle is equally likely to be moving right or left. However, the particle is not at rest because its average kinetic energy is not zero. Finally, the probability density is
|ψ|2=(2/L)sin2(πx/L).
This probability density is largest at location L/2 and is zero at x=0 and at x=L. Note that these conclusions do not depend explicitly on time.
For the particle in the above example, find the probability of locating it between positions 0 and L/4.
- Answer
-
(1/2−1/π)/2=9%
Quantum mechanics makes many surprising predictions. However, in 1920, Niels Bohr (founder of the Niels Bohr Institute in Copenhagen, from which we get the term “Copenhagen interpretation”) asserted that the predictions of quantum mechanics and classical mechanics must agree for all macroscopic systems, such as orbiting planets, bouncing balls, rocking chairs, and springs. This correspondence principle is now generally accepted. It suggests the rules of classical mechanics are an approximation of the rules of quantum mechanics for systems with very large energies. Quantum mechanics describes both the microscopic and macroscopic world, but classical mechanics describes only the latter.


