3.2: Thermodynamic Systems
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Define a thermodynamic system, its boundary, and its surroundings
- Explain the roles of all the components involved in thermodynamics
- Define thermal equilibrium and thermodynamic temperature
- Link an equation of state to a system
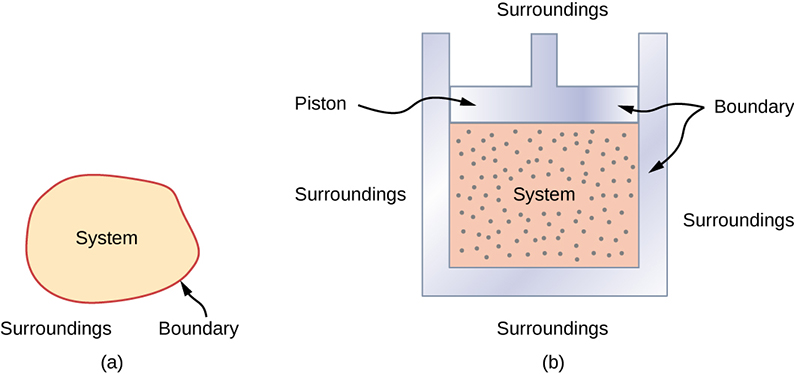
A thermodynamic system includes anything whose thermodynamic properties are of interest. It is embedded in its surroundings or environment; it can exchange heat with, and do work on, its environment through a boundary, which is the imagined wall that separates the system and the environment (Figure 3.2.1). In reality, the immediate surroundings of the system are interacting with it directly and therefore have a much stronger influence on its behavior and properties. For example, if we are studying a car engine, the burning gasoline inside the cylinder of the engine is the thermodynamic system; the piston, exhaust system, radiator, and air outside form the surroundings of the system. The boundary then consists of the inner surfaces of the cylinder and piston.
Normally, a system must have some interactions with its surroundings. A system is called an isolated and closed system if it is completely separated from its environment—for example, a gas that is surrounded by immovable and thermally insulating walls. In reality, a closed system does not exist unless the entire universe is treated as the system, or it is used as a model for an actual system that has minimal interactions with its environment. Most systems are known as an open system, which can exchange energy and/or matter with its surroundings (Figure 3.2.2).

When we examine a thermodynamic system, we ignore the difference in behavior from place to place inside the system for a given moment. In other words, we concentrate on the macroscopic properties of the system, which are the averages of the microscopic properties of all the molecules or entities in the system. Any thermodynamic system is therefore treated as a continuum that has the same behavior everywhere inside. We assume the system is in equilibrium. You could have, for example, a temperature gradient across the system. However, when we discuss a thermodynamic system in this chapter, we study those that have uniform properties throughout the system.
Before we can carry out any study on a thermodynamic system, we need a fundamental characterization of the system. When we studied a mechanical system, we focused on the forces and torques on the system, and their balances dictated the mechanical equilibrium of the system. In a similar way, we should examine the heat transfer between a thermodynamic system and its environment or between the different parts of the system, and its balance should dictate the thermal equilibrium of the system. Intuitively, such a balance is reached if the temperature becomes the same for different objects or parts of the system in thermal contact, and the net heat transfer over time becomes zero.
Thus, when we say two objects (a thermodynamic system and its environment, for example) are in thermal equilibrium, we mean that they are at the same temperature. Let us consider three objects at temperatures T1,T2, and T3 respectively. How do we know whether they are in thermal equilibrium? The governing principle here is the zeroth law of thermodynamics:
If object 1 is in thermal equilibrium with objects 2 and 3, respectively, then objects 2 and 3 must also be in thermal equilibrium.
Mathematically, we can simply write the zeroth law of thermodynamics as
If T1=T2 and T1=T3, then T2=T3.
This is the most fundamental way of defining temperature: Two objects must be at the same temperature thermodynamically if the net heat transfer between them is zero when they are put in thermal contact and have reached a thermal equilibrium.
The zeroth law of thermodynamics is equally applicable to the different parts of a closed system and requires that the temperature everywhere inside the system be the same if the system has reached a thermal equilibrium. To simplify our discussion, we assume the system is uniform with only one type of material—for example, water in a tank. The measurable properties of the system at least include its volume, pressure, and temperature. The range of specific relevant variables depends upon the system. For example, for a stretched rubber band, the relevant variables would be length, tension, and temperature. The relationship between these three basic properties of the system is called the equation of state of the system and is written symbolically for a closed system as
f(p,V,T)=0,
where V, p, and T are the volume, pressure, and temperature of the system at a given condition.
In principle, this equation of state exists for any thermodynamic system but is not always readily available. The forms of f(p,V,T)=0 for many materials have been determined either experimentally or theoretically. In the preceding chapter, we saw an example of an equation of state for an ideal gas,
f(p,V,T)=pV−nRT=0.
We have so far introduced several physical properties that are relevant to the thermodynamics of a thermodynamic system, such as its volume, pressure, and temperature. We can separate these quantities into two generic categories. The quantity associated with an amount of matter is an extensive variable, such as the volume and the number of moles. The other properties of a system are intensive variables, such as the pressure and temperature. An extensive variable doubles its value if the amount of matter in the system doubles, provided all the intensive variables remain the same. For example, the volume or total energy of the system doubles if we double the amount of matter in the system while holding the temperature and pressure of the system unchanged.


